最小生成树算法——Prim

Posted 2022-01-11 爱敲代码的Harrison

P算法流程

一开始图中所有的边都默认被锁住了，只有边被解锁了，才能考虑要不要这条边。一开始图中所有的点也都默认全部被锁住了，只有选中了某个点，这个点才被解锁，并且这个点的直接边（从这个点出发的边）也全部被解锁。解锁的点放入一个集合。

所以，一开始从图中任意一点出发，在这个点的所有直接边里选一条权值最小的边，如果这条边的的两侧有新结点，就解锁这个结点；如果没有新结点，就不要这条边。然后新解锁的结点的直接边又全部被解锁了，再在这些边里面选权值最小的边…周而复始。

总的来说，P算法流程就是，先从某个点出发，解锁一批边，选条最小的边解锁一个新结点，再解锁一批边…

P算法不需要用到并查集，因为总是一个点解锁一批边，在这一批边里选一个点放入集合里。每次都是一个一个点进入集合，根本不存在两大片集合要合并的问题。所以表示解锁的点只需要一个集合就可以。当然边的选择还是要用到小根堆。

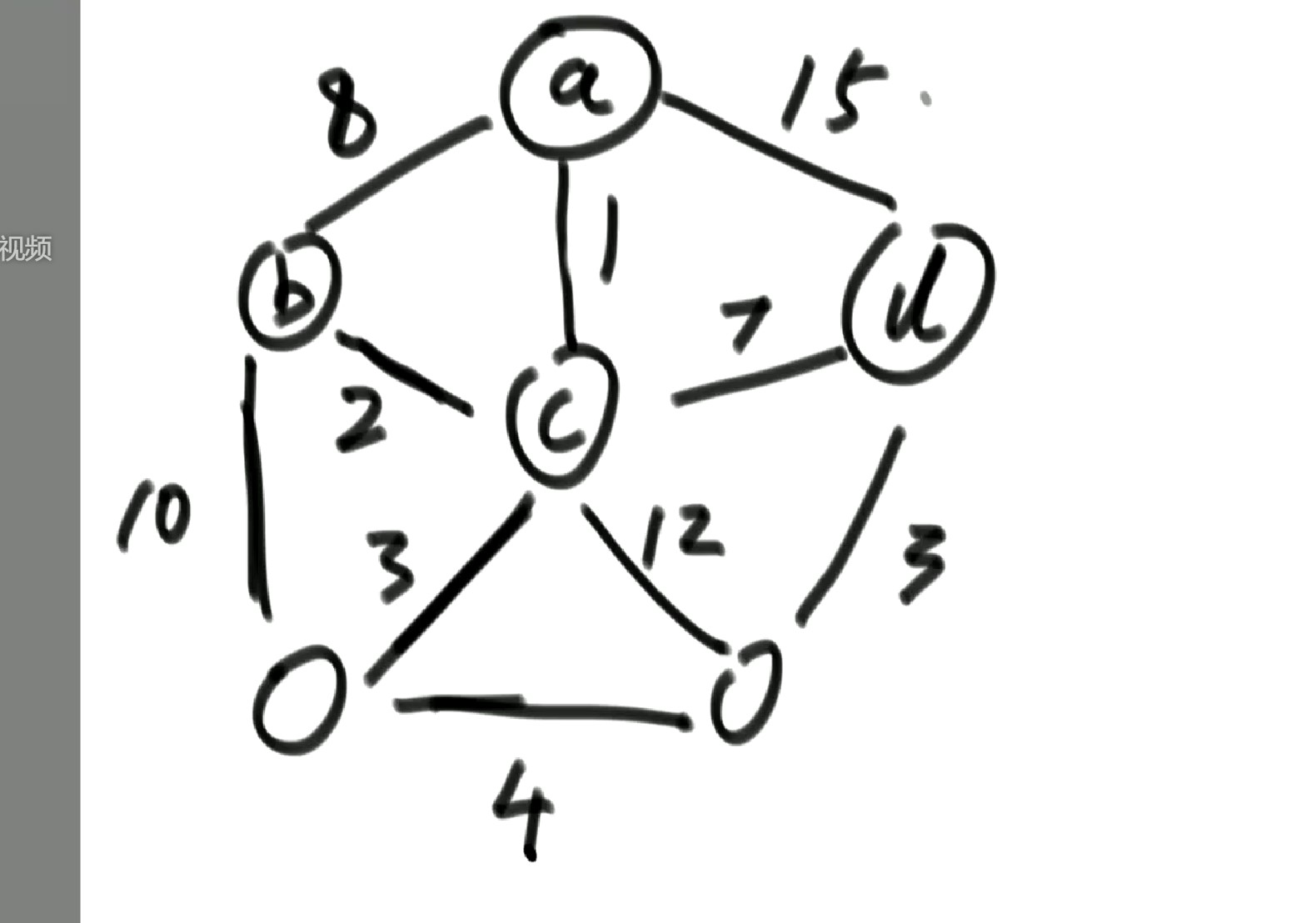
大家可以按照上面的思路和下面图片来理一下思路：

package com.harrison.class11;

import java.util.Comparator;
import java.util.HashSet;
import java.util.PriorityQueue;
import java.util.Set;

import com.harrison.class11.Code01_NodeEdgeGraph.*;

public class Code06_Prim 
	public static class EdgeComparator implements Comparator<Edge>
		public int compare(Edge e1,Edge e2) 
			return e1.weight-e2.weight;
		
	
	
	public static Set<Edge> primMST(Graph graph)
		// 按边的权值组织的小根堆
		PriorityQueue<Edge> pq=new PriorityQueue<>(new EdgeComparator());
		// 解锁的点放入这个集合里
		HashSet<Node> nodeSet=new HashSet<>();
		// 保证放入小根堆里的边不会重复
		HashSet<Edge> edgeSet=new HashSet<>();
		// 选好的边就依次放入这个集合
		Set<Edge> ans=new HashSet<>();
		// for循环只是为了防止森林的出现，也可以去掉此for循环
		// 因为面试题中不会出现森林，不管有向无向
		for(Node node:graph.nodes.values()) 
			if(!nodeSet.contains(node)) 
				nodeSet.add(node);
				for(Edge edge:node.edges) // 接下来由这个点解锁一批边
					if(!edgeSet.contains(edge)) 
						pq.add(edge);
						edgeSet.add(edge);
					
				
				while(!pq.isEmpty()) 
					Edge edge=pq.poll();// 弹出权值最小的边
					Node toNode=edge.to;
					if(!nodeSet.contains(toNode)) 
						nodeSet.add(toNode);
						ans.add(edge);
						for(Edge nextEdge:node.edges) 
							if(!edgeSet.contains(nextEdge)) 
								pq.add(nextEdge);
								edgeSet.add(nextEdge);
							
						
					
				
			
			break;
		
		return ans;
	

最后再总结一下：

1）随便选一个结点解锁，相邻的边也全部解锁，然后选一条权值最小的边

2）新解锁的边两侧有新结点，则把新节点给解锁，并把新解锁的边考虑在最小生成树里面；新解锁的边两侧没有新结点，则不将新解锁的边考虑在最小生成树里面

3）新解锁的结点所有相邻的边被解锁，已经被考虑在最小生成树里的边不重复解锁，然后在所有相邻的边里选择一条权值最小的边，重复步骤 2）周而复始，一直到把所有的点都解锁完