因果推断杂记——因果推断与线性回归SHAP值理论的关系（十九）

Posted 2022-01-06 悟乙己

文章目录

• 1 因果推断与线性回归的关系
• • 1.1 DML的启发
  • 1.2 特殊的离散回归 = 因果？
• 2 因果推断中的ITE 与SHAP值理论的思考
• • 2.1 一些奇思妙想
  • 2.2 因果推断 -> shap值
  • 2.3 ecoml中的shap值的案例
  • • 2.3.1 单干预 - 单输出
    • 2.3.2 多干预 - 多输出

---

1 因果推断与线性回归的关系

第一个问题也是从知乎的这个问题开始：
因果推断（causal inference）是回归（regression）问题的一种特例吗？

其中经济学大佬慧航提到过，回归只是工具，因果推断可以用，其他研究方向也可以用。

在此给出我的看法，

因果推断，是需要考虑干预得（Y|X,T），其中干预效应是主要的差异点；
而一般的多元，只是(Y|X)，并没有考量到干预T的影响

1.1 DML的启发

所以，之前在做DML的时候，可以看到整个异质性HTE的求解经过：
因果推断笔记——DML ：Double Machine Learning案例学习（十六）

我们首先基于X使用ML获得T的残差和Y的残差，之后使用lr拟合残差，不同的是，这次我们把X和T的交互项加进来，即

$Y_i-M_y(X_i)=\tau (X_i)\cdot (T_i-M_t(X_i))+{ϵ}_i$

$\widetilde{Y_i}=\alpha +{\beta }_1\widetilde{T_i}+{\beta \text{β}\beta }_2{X}_i\text{Xi}{X}_i\widetilde{T_i}+{ϵ}_i$

然后我们就可以计算CATE的值了：

$\hat{\mu }(\partial Sale{s}_i,X_i)=M(Price=1,X_i)-M(Price=0,X_i)$

其中，M即最后的lr模型。

从以上DML求解无偏异质性CATE的过程看到，如果要得到无偏解，是需要经过一些求解步骤的；
关于残差正交化可得到无偏差因果效应的数学原理：https://zhuanlan.zhihu.com/p/41993542

1.2 特殊的离散回归 = 因果？

当然，这里感觉有个特例，$（Y|X,T）$ 中 如果不考虑任何协变量的影响，只有$（Y|T）$
那么此时，因果关系的ATE，应该就是等于$（Y|T）$ 离散回归的系数

---

2 因果推断中的ITE 与SHAP值理论的思考

本问题是由 多篇顶会看个体因果推断（ITE）的前世今生
和
机器学习模型可解释性进行到底 —— SHAP值理论（一）
引发的思考。

2.1 一些奇思妙想

本节可不参考，比较胡言乱语…

ITE代表的是无偏个体效应

再来看一下SHAP值中，可以“量化”不同特征，对个体的影响值，那么这个值，可以认为是RM的ITE吗？
虽然，SHAP值肯定是有偏的，但是也想沿着这个问题来看，SHAP值理论中的SHAP代表的怎么样的 “ITE”？在有偏的结论下，该如何解读？
之后简称sITE （此处应该需要公式推导，笔者水平就解读有限了）
个人理解:
$sITE=Predict(Y|X)-Predict(Y|X)的均值$

那么这里的实验组 - 对照组中的对照组就是，模型预测情况下，所有个体的“平均水平”
如果其中有一个特征是，是否有优惠券，

• 特征SHAP值>0，就代表，优惠券对其的刺激，比大家反应要强烈一些，更能刺激购买
• 特征SHAP值<0，代表，优惠券对其的刺激，要弱于常人，不利购买，不建议推送优惠券

沿着这个解读，给一个当下 “不负责任” 的结论： 值有偏，正负方向无偏：

• SHAP值量化出来的sITE 是有偏的，具体的值不具有参考意义；
• 但方向（正负号）代表整体趋势，还是可以借用的。

所以，不知道看到这里的看客，
有木有人，想用SHAP值来直接做“个性化推荐”的？

2.2 因果推断 -> shap值

经过一夜思考，有了一些Update，如下参考：案例：EconML + SHAP丰富可解释性

也就是，如果模型训练集中存在合理的实验组与对照组，且按照某些规范进行组合，那么就形同uplift model中的s-learner的形态（参考：思考：差分响应模型升级版（One-Model Approach）），此时shap值即为无偏，
此时eITE 含义应该就是 -> 某个样本 与 总体均值的处理效应ITE

2.3 ecoml中的shap值的案例

类似于如何用SHAP解释黑箱预测机器学习模型，我们也可以解释黑箱效应异质性模型。这种方法解释了为什么异质因果效应模型对特定人群产生了较大或较小的效应值。是哪些特征导致了这种差异?

当模型被简洁地描述时，这个问题很容易解决，例如线性异质性模型的情况，人们可以简单地研究模型的系数。
然而，当人们开始使用更具表现力的模型(如随机森林和因果森林)来建模效果异质性时，就会变得困难。
SHAP值对于理解模型从训练数据中提取的影响异质性的主导因素有很大的帮助。
我们的软件包提供了与SHAP库的无缝集成。每个CateEstimator都有一个方法shap_values，它返回每个处理和结果对的估计器输出的SHAP值解释。

然后，可以使用SHAP库提供的大量可视化功能对这些值进行可视化。
此外，只要有可能，我们的库就会为每种最终模型类型从SHAP库中调用快速专用算法，这可以大大减少计算时间。

2.3.1 单干预 - 单输出

## Ignore warnings
from econml.dml import CausalForestDML, LinearDML, NonParamDML
from econml.dr import DRLearner
from econml.metalearners import DomainAdaptationLearner, XLearner
from econml.iv.dr import LinearIntentToTreatDRIV
import numpy as np
import scipy.special
import matplotlib.pyplot as plt
import shap
from sklearn.ensemble import RandomForestRegressor, RandomForestClassifier
from sklearn.linear_model import Lasso

np.random.seed(123)
n_samples = 5000
n_features = 10
true_te = lambda X: (X[:, 0]>0) * X[:, 0]
X = np.random.normal(0, 1, size=(n_samples, n_features))
W = np.random.normal(0, 1, size=(n_samples, n_features))
T = np.random.binomial(1, scipy.special.expit(X[:, 0]))
y = true_te(X) * T + 5.0 * X[:, 0] + np.random.normal(0, .1, size=(n_samples,))
X_test = X[:min(100, n_samples)].copy()
X_test[:, 0] = np.linspace(np.percentile(X[:, 0], 1), np.percentile(X[:, 0], 99), min(100, n_samples))


# 因果树估计器
est = CausalForestDML(random_state=123)
est.fit(y, T, X=X, W=W)

# 线性估计器
est = LinearDML(random_state=123)
est.fit(y, T, X=X, W=W)

# 非参数
est = NonParamDML(model_y=RandomForestRegressor(min_samples_leaf=20, random_state=123),
                  model_t=RandomForestRegressor(min_samples_leaf=20, random_state=123),
                  model_final=RandomForestRegressor(min_samples_leaf=20, random_state=123),
                  random_state=123)
est.fit(y.ravel(), T.ravel(), X=X, W=W)

# 双重鲁棒学习
est = DRLearner(model_regression=RandomForestRegressor(min_samples_leaf=20, random_state=123),
                model_propensity=RandomForestClassifier(min_samples_leaf=20, random_state=123),
                model_final=RandomForestRegressor(min_samples_leaf=20, random_state=123),
                random_state=123)
est.fit(y.ravel(), T.ravel(), X=X, W=W)

# 元学习 DomainAdaptationLearner
est = DomainAdaptationLearner(models=RandomForestRegressor(min_samples_leaf=20, random_state=123),
                              final_models=RandomForestRegressor(min_samples_leaf=20, random_state=123),
                              propensity_model=RandomForestClassifier(min_samples_leaf=20, random_state=123))
est.fit(y.ravel(), T.ravel(), X=X)

# Xlearner 元学习
# Xlearner.shap_values uses a slow shap exact explainer, as there is no well defined final model
# for the XLearner method.
est = XLearner(models=RandomForestRegressor(min_samples_leaf=20, random_state=123),
               cate_models=RandomForestRegressor(min_samples_leaf=20, random_state=123),
               propensity_model=RandomForestClassifier(min_samples_leaf=20, random_state=123))
est.fit(y.ravel(), T.ravel(), X=X)

# 工具变量 
est = LinearIntentToTreatDRIV(model_y_xw=RandomForestRegressor(min_samples_leaf=20, random_state=123),
                              model_t_xwz=RandomForestClassifier(min_samples_leaf=20, random_state=123),
                              flexible_model_effect=RandomForestRegressor(min_samples_leaf=20, random_state=123),
                              random_state=123)
est.fit(y.ravel(), T.ravel(), Z=T.ravel(), X=X, W=W)

输出一个图来看：

est = CausalForestDML(random_state=123)
est.fit(y, T, X=X, W=W)
shap_values = est.shap_values(X[:20])
shap.plots.beeswarm(shap_values['Y0']['T0'])

详细的SHAP可参考：机器学习模型可解释性进行到底 —— SHAP值理论（一）

特征密度散点图：beeswarm

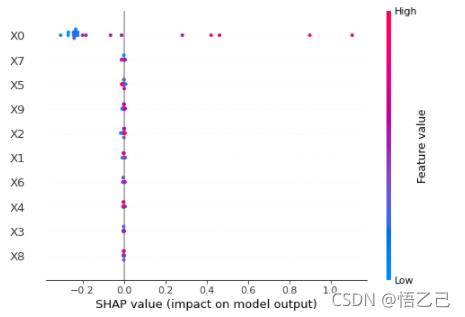
下图中每一行代表一个特征，横坐标为Shap值。特征的排序是按照shap 的平均绝对值，对模型来说的最重要特征。宽的地方表示有大量的样本聚集。

一个点代表一个样本，颜色越红说明特征本身数值越大，颜色越蓝说明特征本身数值越小。

可以看做一种特征重要性的排列图，从这里可以看到X0重要性高（排位）；
同时，X0值越大，对模型的效果影响越好（SHAP值为正）

2.3.2 多干预 - 多输出

# 数据生成
np.random.seed(123)
n_samples = 5000
n_features = 10
n_treatments = 2
n_outputs = 3
true_te = lambda X: np.hstack([(X[:, [0]]>0) * X[:, [0]],
                               np.ones((X.shape[0], n_treatments - 1))*np.arange(1, n_treatments).reshape(1, -1)])
X = np.random.normal(0, 1, size=(n_samples, n_features))
W = np.random.normal(0, 1, size=(n_samples, n_features))
T = np.random.normal(0, 1, size=(n_samples, n_treatments))
for t in range(n_treatments):
    T[:, t] = np.random.binomial(1, scipy.special.expit(X[:, 0]))
y = np.sum(true_te(X) * T, axis=1, keepdims=True) + 5.0 * X[:, [0]] + np.random.normal(0, .1, size=(n_samples, 1))
y = np.tile(y, (1, n_outputs))
for j in range(n_outputs):
    y[:, j] = (j + 1) * y[:, j]
X_test = X[:min(100, n_samples)].copy()
X_test[:, 0] = np.linspace(np.percentile(X[:, 0], 1), np.percentile(X[:, 0], 99), min(100, n_samples))

# 
est = CausalForestDML(n_estimators=400, random_state=123)
est.fit(y, T, X=X, W=W)

#
shap_values = est.shap_values(X[:200])

# 
plt.figure(figsize=(25, 15))
for j in range(n_treatments):
    for i in range(n_outputs):
        plt.subplot(n_treatments, n_outputs, i + j * n_outputs + 1)
        plt.title("Y, T".format(i, j))
        shap.plots.beeswarm(shap_values['Y' + str(i)]['T' + str(j)], plot_size=None, show=False)
plt.tight_layout()
plt.show()

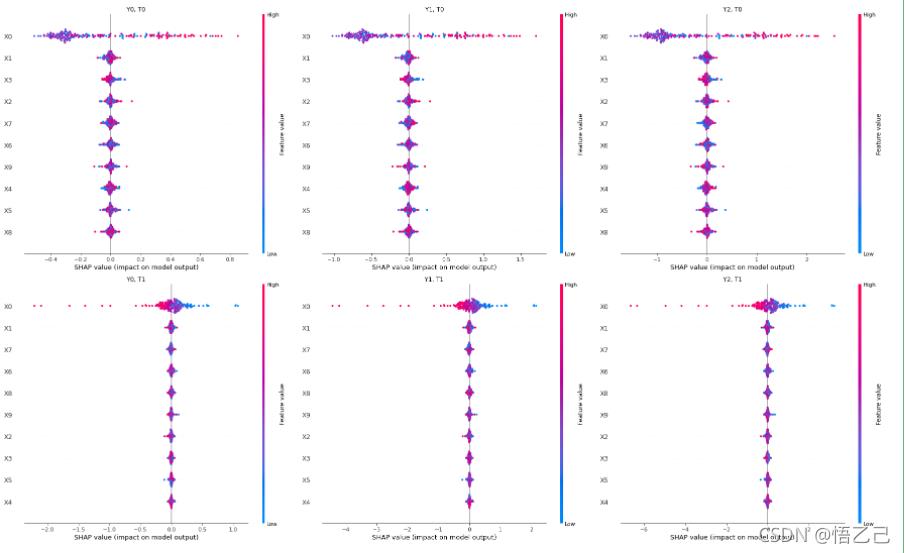
这里可以看到有生成了三个outcome，
两个干预T，直接使用CausalForestDML因果树估计器，
所以就有6种情况可以得到：