投资学实务翻译

Posted 2022-01-06 LESLIEHEE

电力远期的定价

电力市场的周转已变得越来越重要。根据位于德国的欧洲能源贸易联盟(EFET)的数据，2004年已超过2500太瓦时。这相当于德国用电量的五倍，相当于大约750亿德国人。英国的营业额略低于2500太瓦时;在斯堪的纳维亚国家，2004年是2000 TWh。仅在欧洲领先的交易所，莱比锡的能源交易所EEX, 2005年的营业额为602 TWh，这意味着比前一年增加了52%。除了EEX，欧洲其他重要的能源交易所有法国的Powernext、意大利的IPEX、荷兰的APX、奥地利的EXAA、波兰的PolPX、斯堪的纳维亚的Nordpool、斯洛文尼亚的Borzen、西班牙的OMEL和英国的UKPX。2006年1月，来自17个国家的133家公司在EEX交易能源。

通常情况下，电力价格在一天中波动很大。在晚上，价格通常只有白天价格的一半。尤其是在上午10点到下午1点以及下午5点到9点之间，可以观察到价格峰值。这种好奇心是由于电的不可储存性。它必须立即被消耗掉。因此，当家庭用电量特别高时，就会出现峰值价格。因此，能源交易所为高峰负荷(8小时至20小时)和基本负荷(0小时至24小时)提供不同的合同。

能源交换和与能源有关的产品日益重要，这也反映在关于这一问题的文献越来越多。由于能源是不可存储的，Gibson和Schwartz以及Schwartz提出的传统的商品期货估值模型的适用性是有限的。最近，文献中提出了几种新的电力建模方法。特别是Bessembinder和Lemmon提出的模型在文献中得到了广泛的关注。导出了一个可检验的电力远期合约定价方程，该方程必须满足经济均衡条件。因此，我们关注这个模型。在介绍传统的远期定价方法的基础上，讨论了电力远期的定价问题，并给出了一个具体的算例。

传统的远期定价

传统的衍生品合约定价方法是无套利定价方法。考虑远期合约。在这种合同中，双方同意在未来的某个时间点买卖某一特定商品。交换货物必须支付的价格今天确定。这份合同是有约束力的承诺。无论未来市场情况如何，卖方必须交付产品，买方必须支付商定的远期价格。

为了了解远期是如何工作的，让我们以欧洲股市指数EURO STOXX 50的远期为例。欧元斯托克50指数可以看作是由欧洲50家最大公司组成的一个篮子。当然，欧元STOXX 50不能直接买卖，但我们可以假设，我们可以通过直接投资相关股票，很容易地复制它。附录25.1说明了我们双方应根据无套利的考虑来协商远期价格。这个例子反映了2007年2月27日观察到的市场数据。欧元斯托克50指数为4157点，年利率为4%。让我们假设远期合约的结算时间是2007年9月21日(0.5644年后)，远期价格为4500。

这种情况就产生了套利机会。我们怎么看?把你自己放在远期合约的卖方的位置上。她今天可能会以4,157欧元的价格买入欧元斯托克50指数。为了为交易融资，她可以以无风险利率(4%)从银行借同样数量的钱。因此，在2007年9月21日，她可以以4500欧元的价格交付欧元斯托克50。然而，她必须偿还银行的债务，总计达

 

2007年2月27日为欧元STOXX 50期货合约定价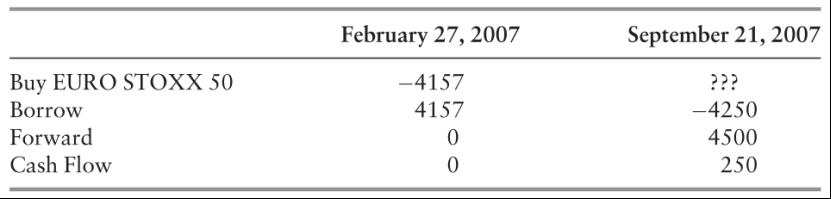

 

注:欧元STOXX 50: 4,157；无风险利率:每年4%；到期日:2007年9月21日(206天)，期货价格:4500。

她可能会保留4500-4250=250的差额。请注意，为了产生这种(无风险的)现金流，没有必要进行初始投资。换句话说，这250个粒子是“凭空产生的”。显然，在运转良好的资本市场，这种情况不可能持续下去:在这种“好得令人难以置信”的交易中，每个人都想成为卖家。因此远期价格会下降(每个人都卖出)，直到4250。

同样地，我们可以证明远期合约不能少于4250。换句话说，考虑无套利因素，远期价格与现货价格挂钩。它必须等于现货价格复合结算日期。然而，请注意，这种无套利的说法之所以有效，只是因为在这种情况下，卖方可以在今天购买欧元STOXX 50并将其存储起来。因此，我们可以肯定我们可以把这个模型应用到大多数的实物上。有时，当涉及到存储成本时，计算必须做一点调整。然而，一般的考虑仍然没有改变。

示例中描述的远期合约是一种非常简单的合约。为便于说明，我们假设不涉及信用风险;也就是说，卖方和买方将交付欧元STOXX 50和钱是没有不确定性的。事实上，事情并没有那么简单。这也是市场参与者经常在欧洲期货交易所(EUREX)等交易所交易衍生品的原因之一。欧洲期货交易所承担交易对手风险。市场参与者不必担心合约的达成。所谓的“期货合约”在衍生品交易所交易，而不是远期合约。期货合约的建立与远期合约略有不同，但在经济上两者非常相似。例如，在利率不变的简化假设下，期货价格与远期价格是相同的。这种关系是由类似上述的无套利考虑来保证的。

电力远期价格

如前所述，电在物理上不能储存。必须制定一种替代办法，以便为远期电力合同定价。Bessembinder和Lemmon的方法明确地提供了模型以及对远期合约的需求。模型的一般设置概述在附录25.2中。电力市场由非电力生产者和非电力零售商组成。生产者生产的电力可以在批发市场上卖给零售商。这个市场没有规定，价格由生产商和零售商独立协商。零售商自己与最终消费者签订合同。Bessembinder-Lemmon模型采用两期模型。今天，零售商和消费者就一个固定的价格达成一致，消费者可以想消耗多少能量就消耗多少。下一阶段所消耗的总能量是随机的。例如，如果下一段时间是夏天，我们不知道天气是热还是冷。如果我们有一个炎热的夏天，那么消费者打开他们的空调，消耗大量的能源。如果夏天又冷又多雨，则情况正好相反。

零售商面临的不确定性。他们不知道下一时期消费者的总需求。由于电不能储存，它必须在消耗的同时产生。因此，更高的消费者需求必然导致批发市场上更高的需求。这反过来又会导致更高的价格。每单位电力的交易保证金是批发市场(随机)上从生产者购买电力和向消费者出售电力的价格之间的差额。因此，消费者需求的增加是模棱两可的。零售商向消费者销售更多的电力。如果交易保证金为正值，这将产生积极的影响。另一方面，批发市场的价格上涨，交易的利润减少。

类似地，生产者也面临着不确定性:他们还受到与消费者需求相关的风险的影响。然而，他们并不担心批发现货市场的价格上涨。价格和需求的增加都导致生产者的销售增加。

为了对冲价格风险，生产者和零售商可以签订远期电力合同;也就是说，他们今天可以商定一个价格，在这个价格上，他们愿意在下一个时期在批发市场上交易电力。正如我们稍后将看到的，他们选择远期价格以便生产者和零售商都优化他们的风险/预期回报概况。

综上所述，我们将区分以下变量:

 

最终目标是今天确定远期价格。因此，我们必须首先分析下一个时期，以建立消费者总需求与批发(现货)价格之间的关系。在第二步中，我们可以计算远期价格作为市场出清价格，当生产者和零售商优化他们的风险/预期利润配置。

第二阶段批发价格的确定

起点是生产者的总成本函数。总成本取决于在现货批发市场上出售的数量和通过远期合同签订的电力远期定价。我们作出假设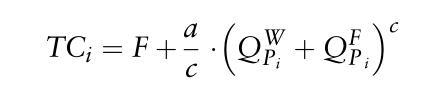

 

其中，F是固定成本，a和c是可变成本参数(c≥2)。总成本函数的形状如图所示。能源的生产伴随着边际成本的增加。

生产者的利润等于批发和远期交易的总收入减去总成本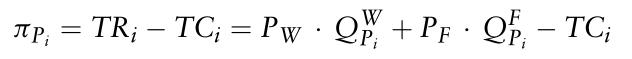

 

从标准微观经济学理论中，我们知道在一定的现货批发价格下，如何确定生产者应提供的最优数量。我们要做的就是设置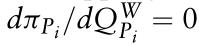。经过一些计算，我们得到

 

 

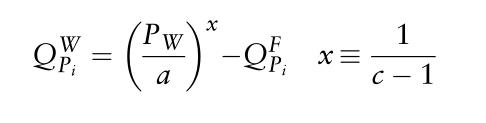
为了确定最优的批发价格，电力的供求量必须是均衡的。

从直观上看，这是一种激励生产者提供必要电量以满足消费者需求的价格。这种关系符合经济直觉:消费者的需求越高，批发现货市场的价格就越高。

第一阶段远期价格的确定

在下面，我们假设生产者和零售商都是风险规避者。更准确地说，我们将生产者的目标函数定义为

 

直觉上，生产者喜欢更高的预期利润，因为它们增加了目标函数。相反，他们不喜欢以差异利润为特征的不确定性。系数越大，他们的厌恶程度就越高。因此，awe可以控制市场参与者的风险规避。将成本函数(25.1)、最优批发数量(25.3)和批发价格(25.5)代入利润函数(25.2)，得到预期利润

 

 

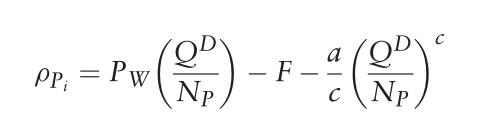
代表批发现货交易的利润和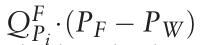远期交易的利润。当考虑两个随机量之间的协方差时，可以计算出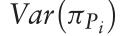更准确地说，方差是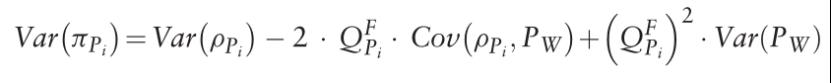

 

 

 

最后，通过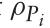的定义可以确定两个随机变量之间的协方差

 

 

利用这些中间结果，我们可以最大化生产者的目标函数。因此，我们计算目标函数关于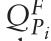的一阶导数并将其设为零。考虑(25.8)和(25.9)，我们可以确定在给定市场远期价格的情况下，生产者将远期销售的最优数量。对于生产来说，结果是

 

 

直观地说，这是在远期价格的情况下，为了最大化风险/预期回报，生产者应该卖出的远期数量。

接下来，我们可以计算零售商j的最优远期销售量。我们假设与生产者的目标函数相同。也就是说,

 

类似于对生产者的计算表明，在市场远期价格的条件下，当前最优的远期销售量是

 

这个数量保证了零售商优化他们的风险/预期回报。在(25.12)中，零售商的现货交易的利润来自于销售价和买入价之间的差额;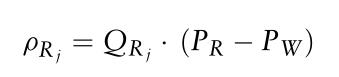

 

式(25.10)和式(25.14)是非常重要的结果。它们显示在给定特定远期价格的情况下，生产者和零售商的远期销售量。在均衡状态下，远期合约的净供给为零(也就是说，对于远期合约中的每一个卖方，我们都应该找到一个买方)。从数学上讲，这意味着所有远期销售数量的总和必须等于零。因此，我们得到平衡条件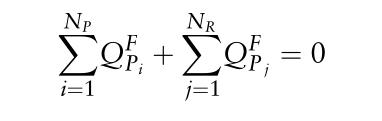

 

使用公式(25.10)和(25.14)，并进行一些代数变换(如本章附录A所示)，可以得到预期的均衡远期价格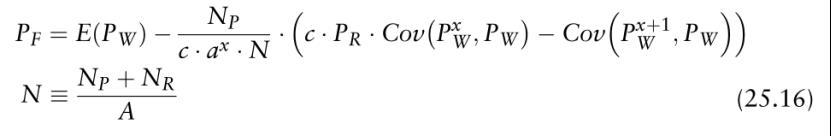

 

因此，电力的均衡远期价格取决于预期批发价格和两个协方差表达式。

不幸的是，尤其是方程(25.16)中的协方差很难处理。本章附录B进一步简化了(25.16)中的两个协方差表达式。它们导致了远期价格的一个非常容易处理的近似

一个数值应用程序

    

 

为了更详细地调查消费者需求、批发市场价格和远期价格之间的关系，我们现在转向模型的数值实现。模型参数如表25.4所示。参数值的选择类似于Lemmon和Bessembinder使用的方法。由于(25.1)中的固定成本参数F不影响批发数量和进一步的结果，所以我们不必须对它做出任何假设。消费者需求正态分布，均值为100，方差为20。此外，我们假设零售商将现货价格设为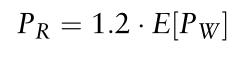

 

因此，直觉上，零售商在预期批发价的基础上增加了20%的安全缓冲。在本例中，零售商的数量等于供应商的数量(=10)。

第一步，我们必须确定下一个时期的批发价格的分配。因此，我们进行蒙特卡罗模拟，根据正态概率分布考虑1000个随机情景的未来消费者需求。一旦我们知道了消费者的需求，我们可以立即根据公式(25.5)计算出批发价。

表25.5显示了前18个模拟的消费者需求和相应的批发价格。例如，第一个批发价仅仅是考虑128.97的需求而给出的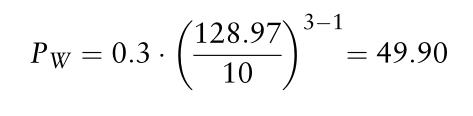

 

以类似的方式，我们可以继续进行所有其他模拟。总共有1000种未来批发市场现货价格的情况。从这些情形中，我们可以计算算术平均值、方差和偏态，以估计批发价格分布的均值、方差和偏态。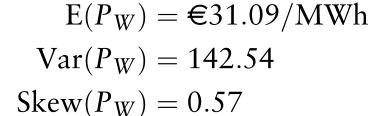

 

结果是

 

远期价格比现货价格低8倍以上。这种关系在其他商品远期和期货市场中也经常观察到。当远期价格低于预期现货价格时，这种现象被称为现货溢价。现货溢价现象通常发生在基础产品价格昂贵时石油一旦从地下开采出来，就会造成巨大的储存成本。

然而，在电力转发的情况下，我们不能把这种折扣与存储成本联系起来。相反，折扣主要是由于批发价格的差异。显然，它与生产者和零售商的套期保值需求有关。一般来说，两者都能从批发市场价格的上涨中获利(尽管，如上所述，由于零售商的交易保证金缩水，其影响并不明显)。因此，双方都对出售远期合约感兴趣，这将导致远期合约价格的折扣。相比之下，价格上涨对零售商不利，因为他们随后会以低于生产成本的价格向消费者提供电力。这在相反的方向创造了对冲需求(即诱导远期购买)。因此，远期价格与偏度之间的关系是正的。

结论

对远期合约进行估价的通常方法是无套利方法。这种方法不能应用于不可储存的物体，它是它的，它是它的，它是它的，它是它的，它是它的，它是它的。电力转发器必须用不同的型号来定价。Bessembinder-Lemmon模型是一个平衡模型。在该模型中，现货远期市场的供需均为均衡。这使得Bessembinder和Lemmon可以推导出均衡远期价格。均衡价格可以用批发价格分布的前三个矩来近似。

本章表明，与预期批发价格相比，电力远期可能会偏向向下。这是由于对冲需求。在考虑的例子中，远期价格对批发价格的方差的反应是消极的，对它们的偏态是积极的。