二分搜索树实现
Posted guardwhy
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了二分搜索树实现相关的知识,希望对你有一定的参考价值。
1.1 基本介绍
二叉搜索树是二叉树的一种,是应用非常广泛的一种二叉树,英文简称为BST又被称为:二叉查找树、二叉排序树,任意一个节点的值都大于其左子树所有节点的值,任意一个节点的值都小于其右子树所有节点的值,它的左右子树也是一棵二叉搜索树。二叉搜索树可以大大提高搜索数据的效率,二叉搜索树存储的元素必须具备可比较性。
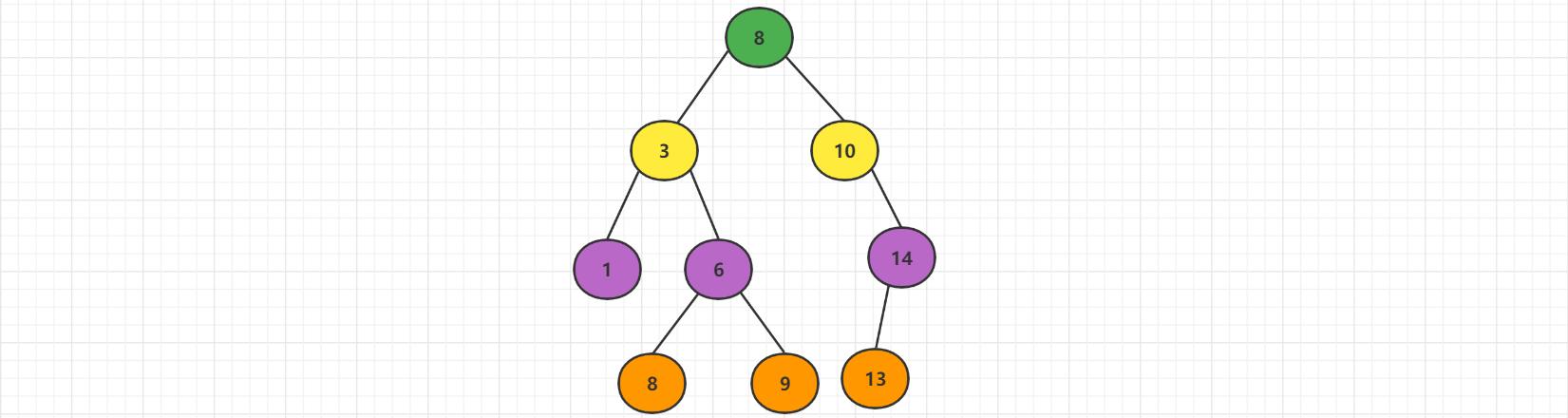
1.2 存储结构
1、顺序存储
二叉树的顺序存储结构就是用一维数组存储二叉树中的结点,并且结点的存储位置,也就是数组的下标要能体现出之间的逻辑关系。
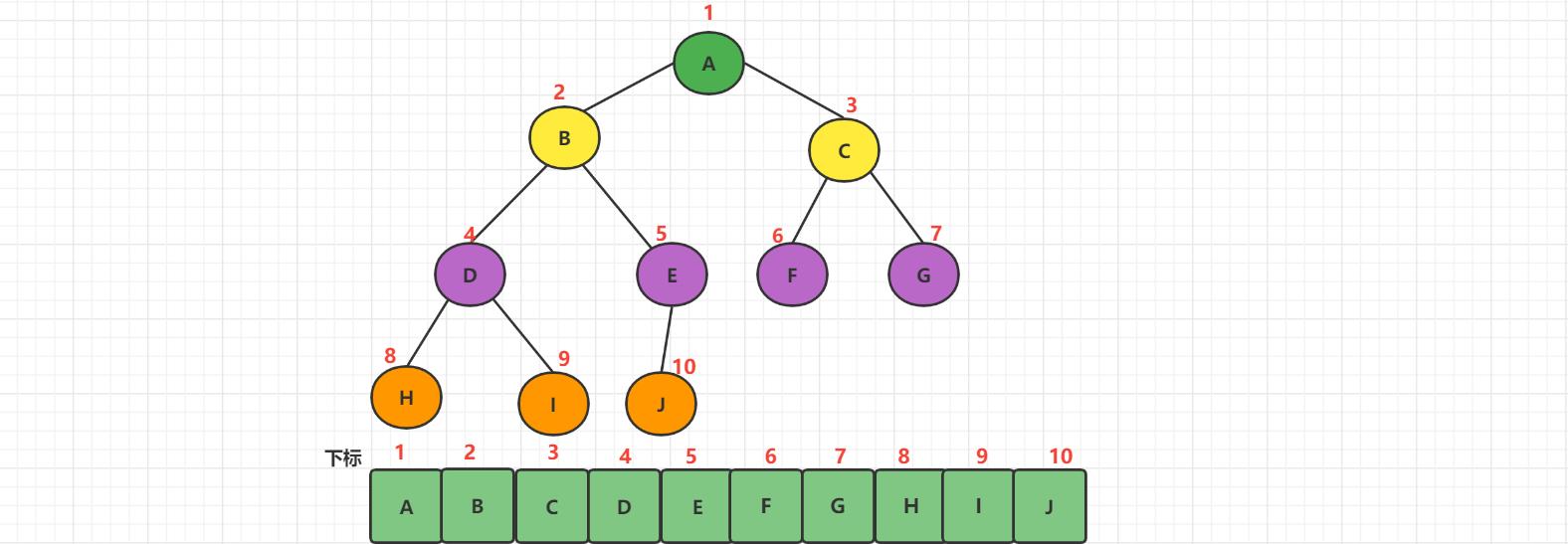
顺序存储结构在极端情况下浪费空间,只适合平衡树的存储。
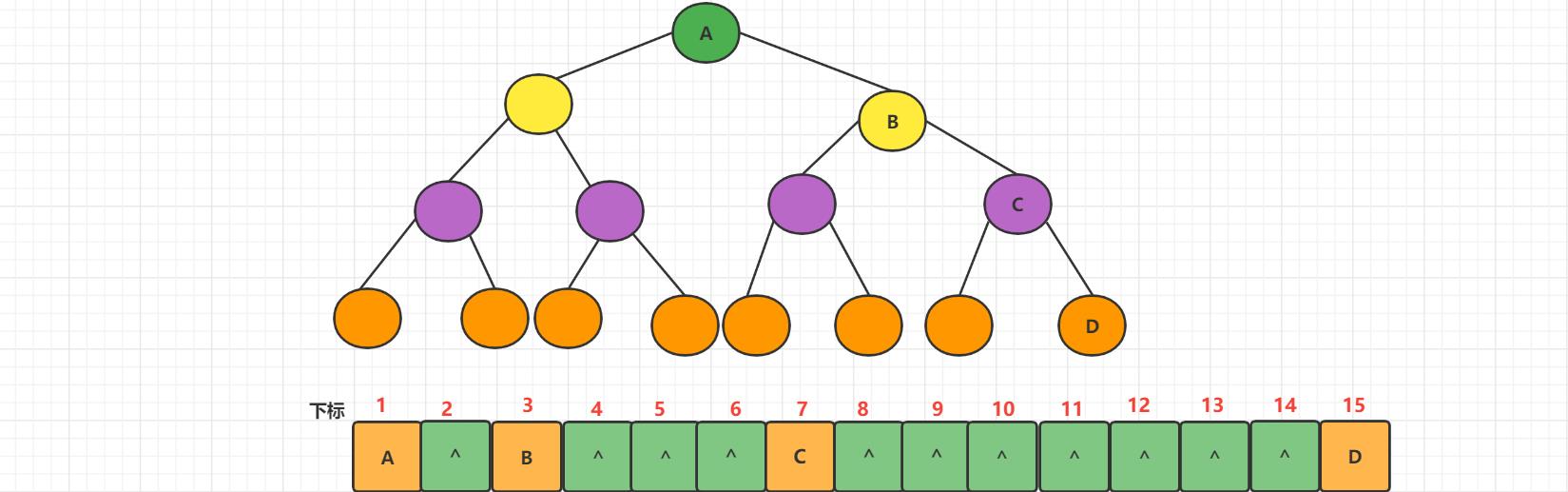
2、链式存储
既然顺序表存储适用性性不强,则考虑链式存储结构,二叉树每个结点最多有两个孩子,所以为它设计一个数据域和两个指针域,这种链表也叫作二叉链表。

其中data是数据域,lchild和rchild都是指针域,分别存放指向左孩子和右孩子的指针。二叉链表示意图如下:
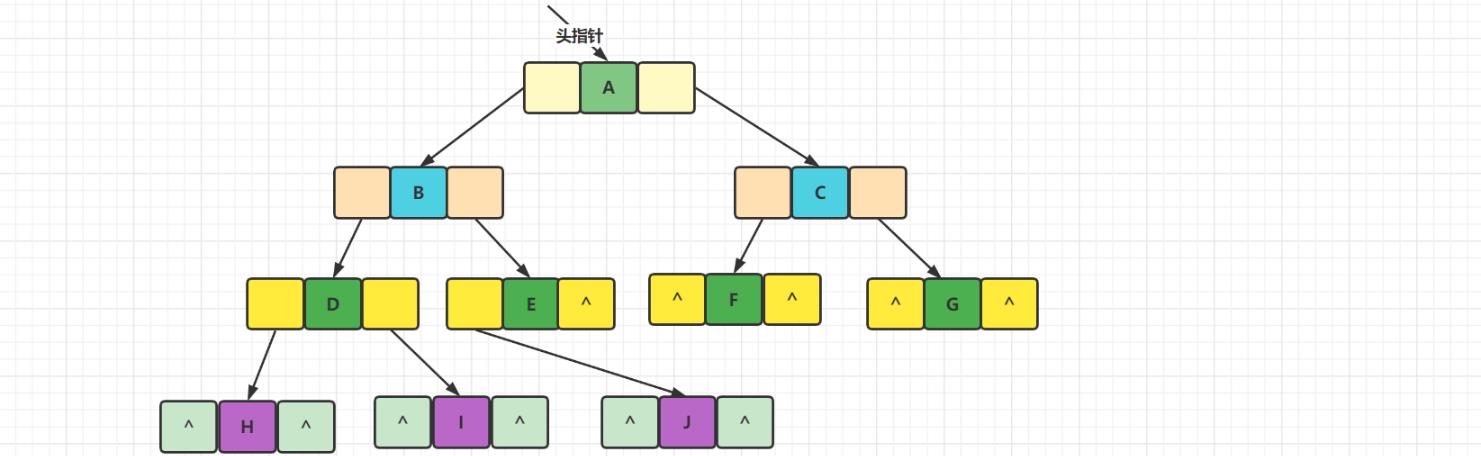
1.3 添加结点
1、思路分析
如果当前二分搜索树一个元素都没有,添加一个新元素【43】,则当前元素为根结点。

二次添加新元素比如添加【23】和【59】,直接让它跟根节点进行比较,大于插入根节点右边,小于插入根节点左边。

依次添加元素
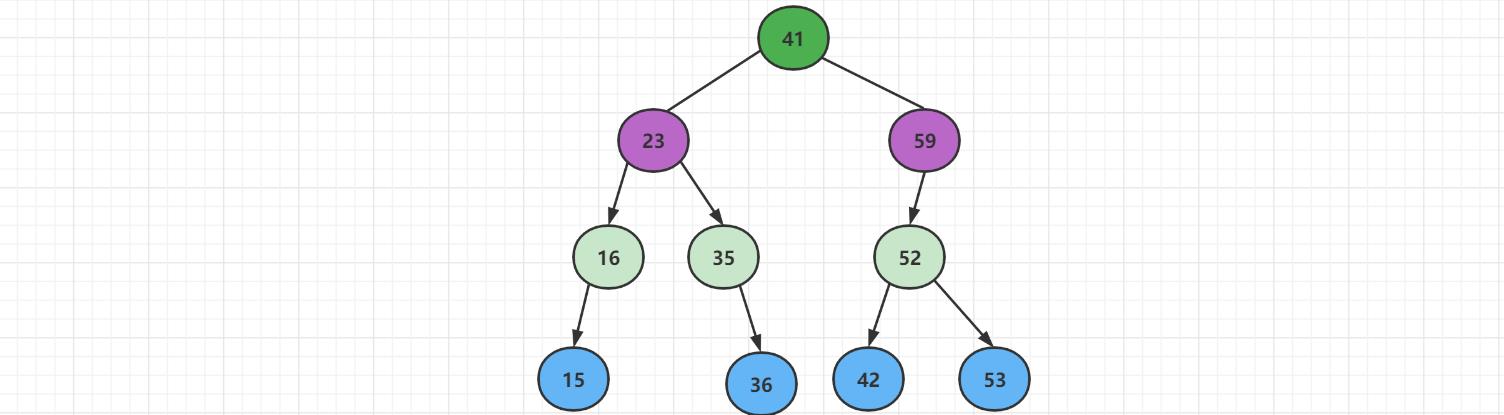
再次添加元素,添加【60】这个新节点,先跟根结点【41】比较,发现【60】比根结点大,插入根节点的右边,继续跟右边结点【59】比较,发现大于【59】,则插入到【59】的右边。
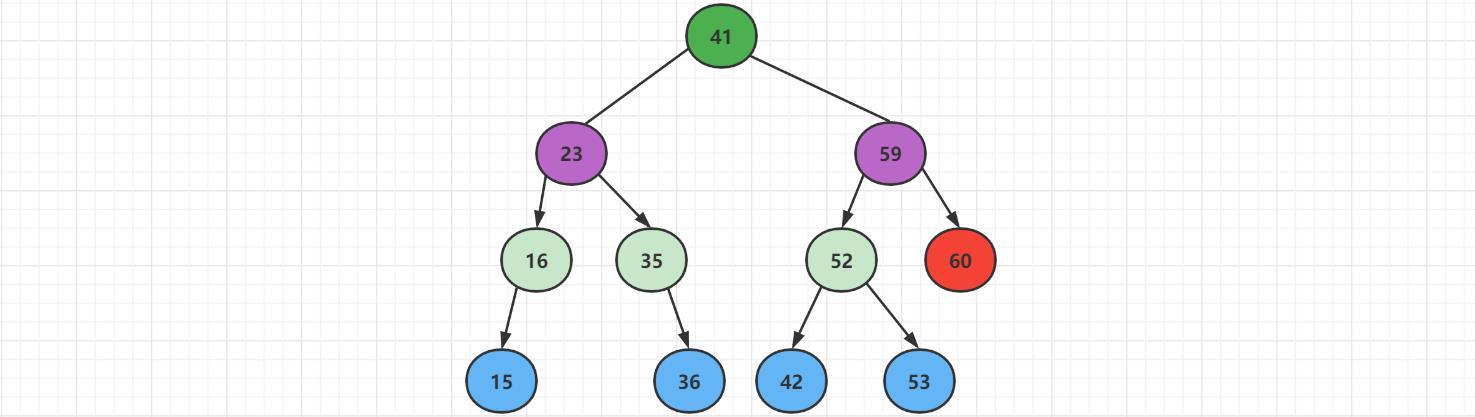
再次插入【28】这个新节点,先跟根结点【41】进行比较,发现小于根结点,往左边插入。一直比较,最终插入到结点【35】的左边。
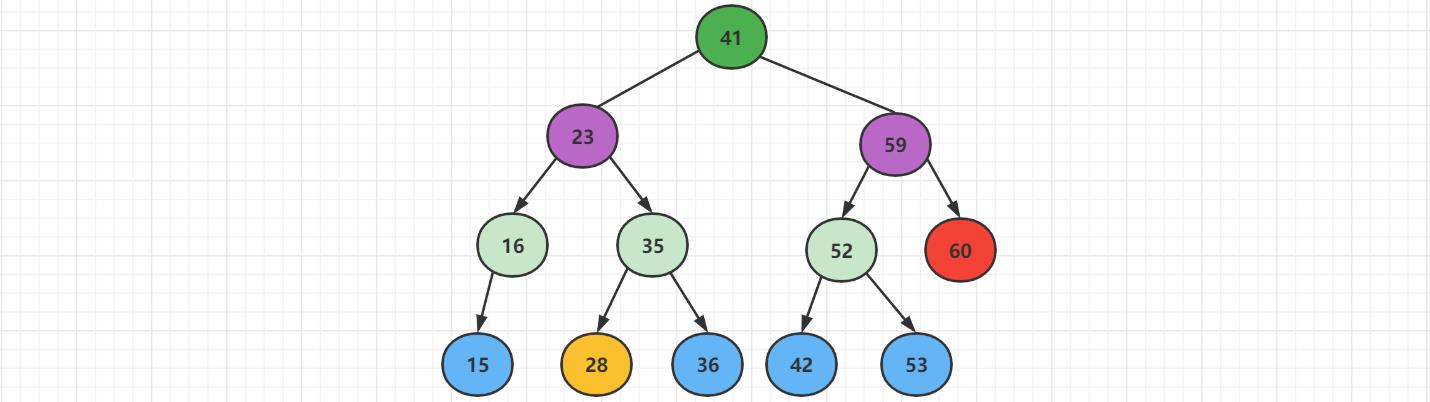
1.4 删除结点
删除二分搜索树最小值
所谓二分搜索树的最小值,一定是一颗二叉树从根节点开始,不停的向左走,直到走不动为止,那个最左的节点一定是最小值。
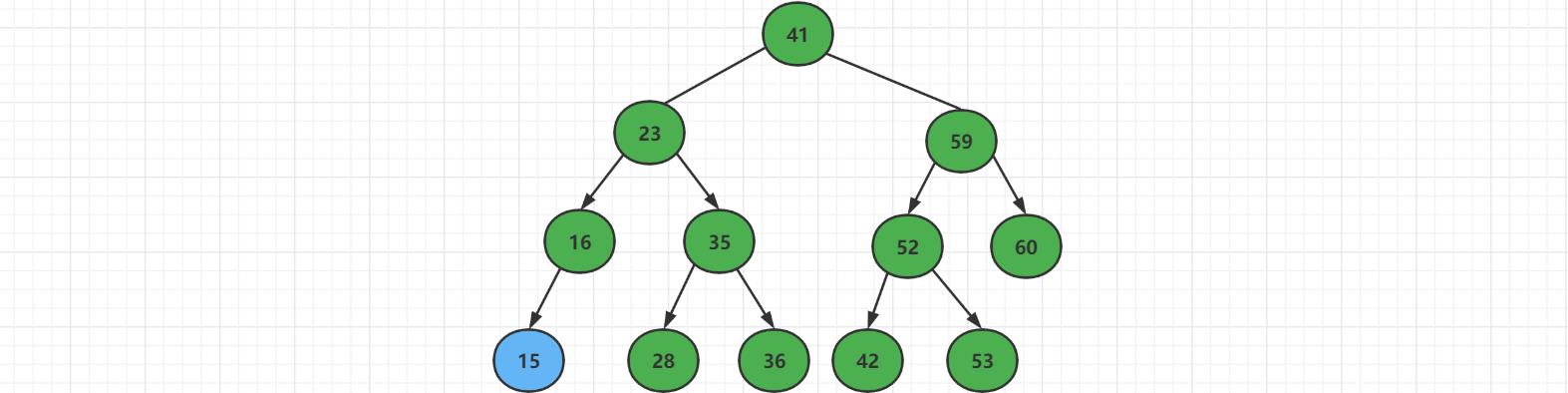
对于上面这颗二叉搜索树来说,删除最小节点,直接删除就好了。
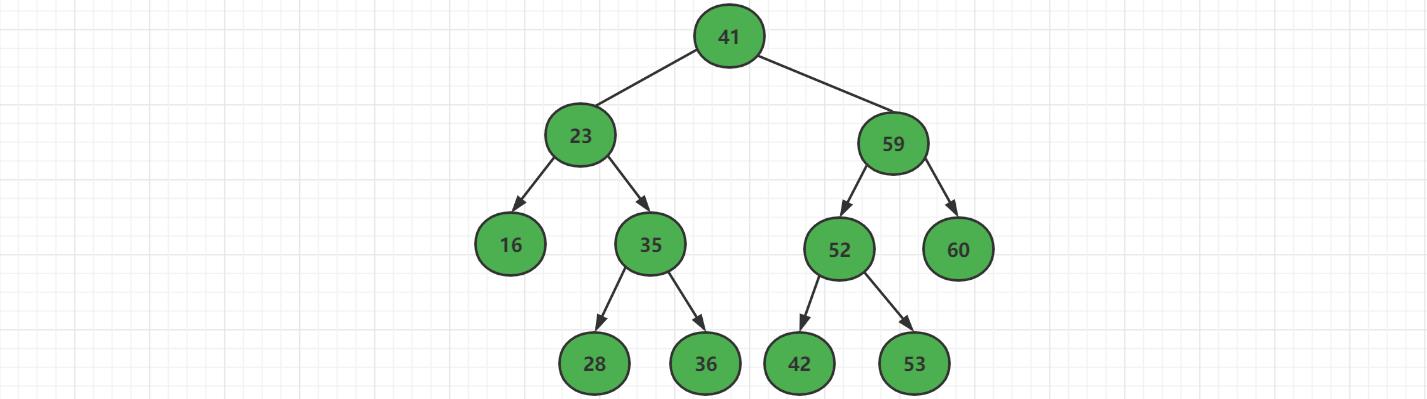
特殊情况,此时二分搜索树最小节点是【23】,该节点存在叶子数。
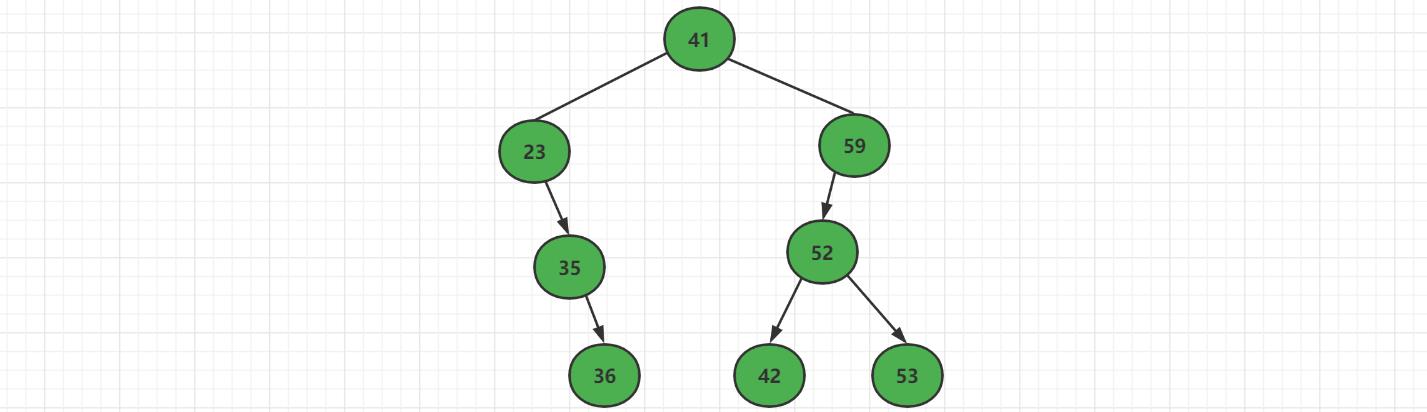
此时只需要将【23】这个节点删除,然后将【23】整个右子树直接接上根结点的左子树就好了。
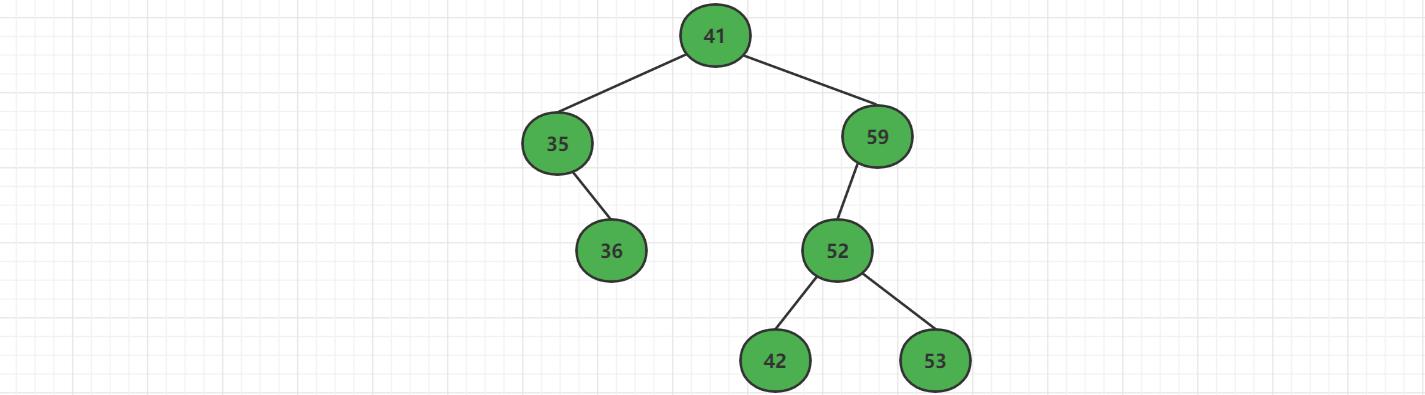
删除二分搜索树最大值
对于下面这颗二叉搜索树来说,删除最大节点【如果是叶子节点】,直接删除就好了。
删除叶子结点成功
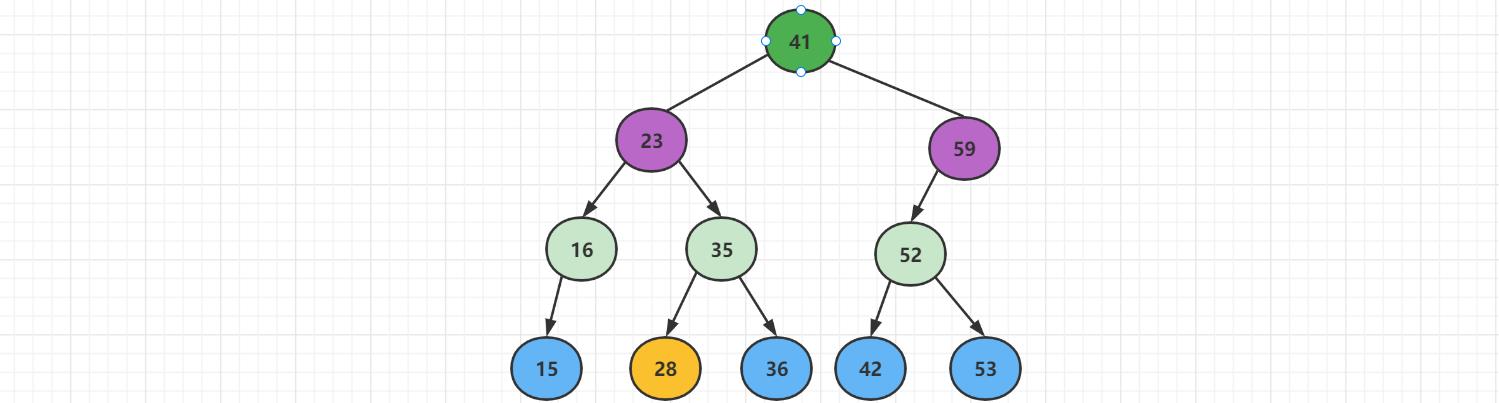
如果不是叶子节点,存在左子树。先将结点【59】删除,然后将58的左子树整体当成41的右子树,接上即可。
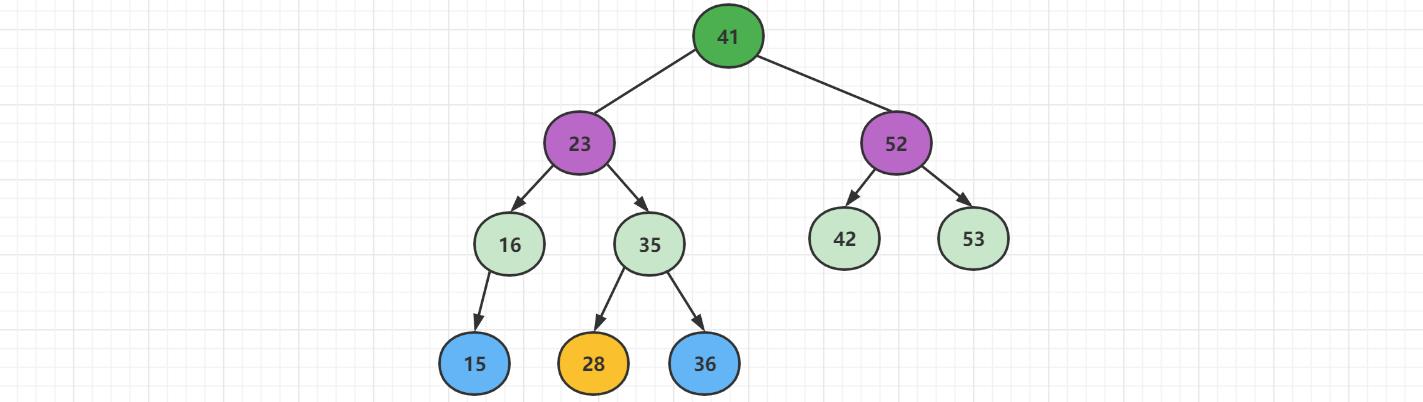
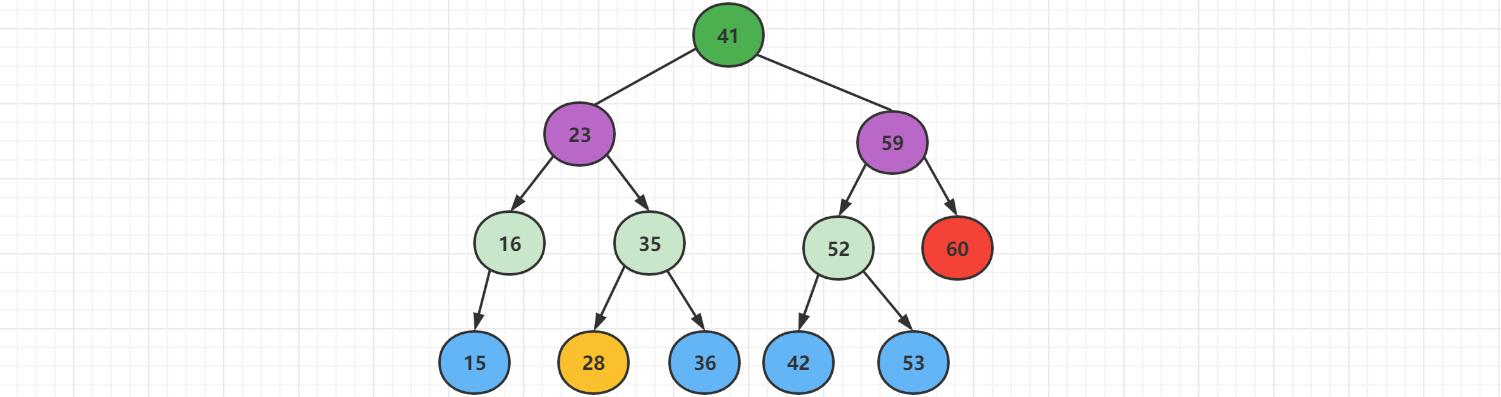
删除二分搜索树任意节点
比如删除58这个节点,该节点左右都有孩子的节点,假设删除的结点为d。
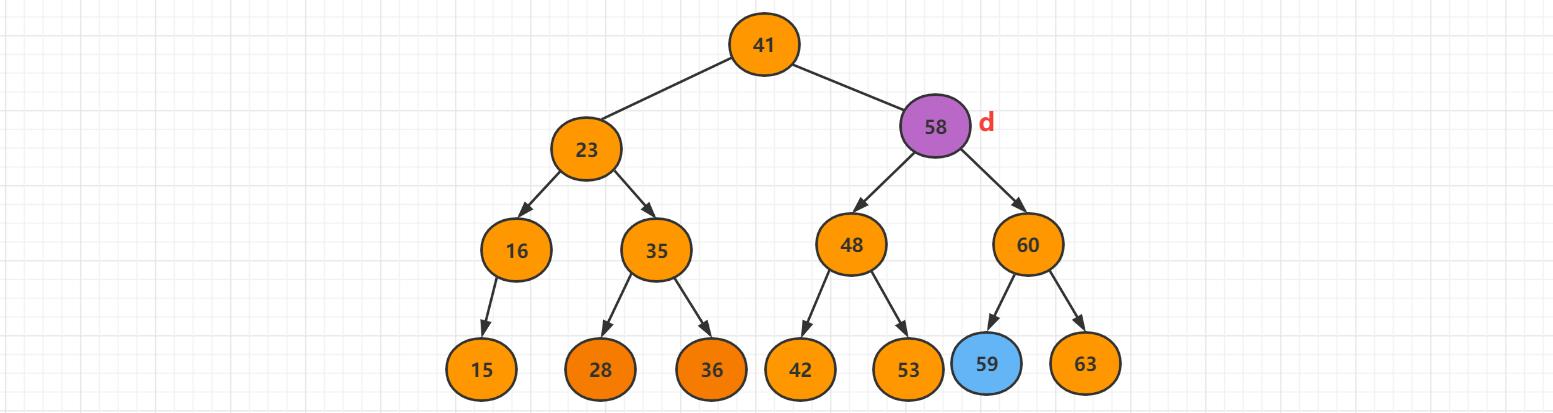
先找到删除节点的右子树的相应最小值的结点,s = min(d->min),s 节点是d的后继,然后在d的右子树中,删除最小的值。
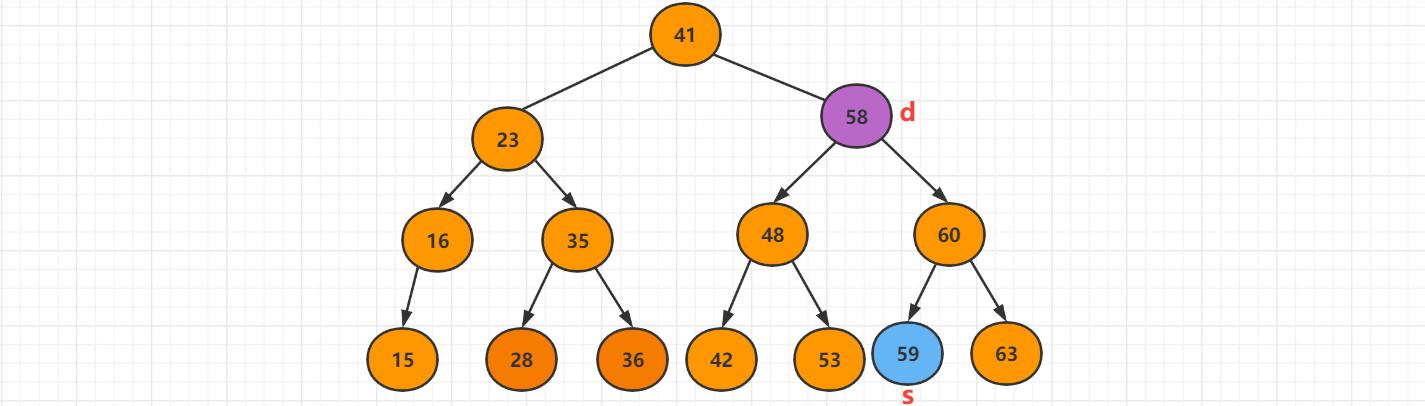
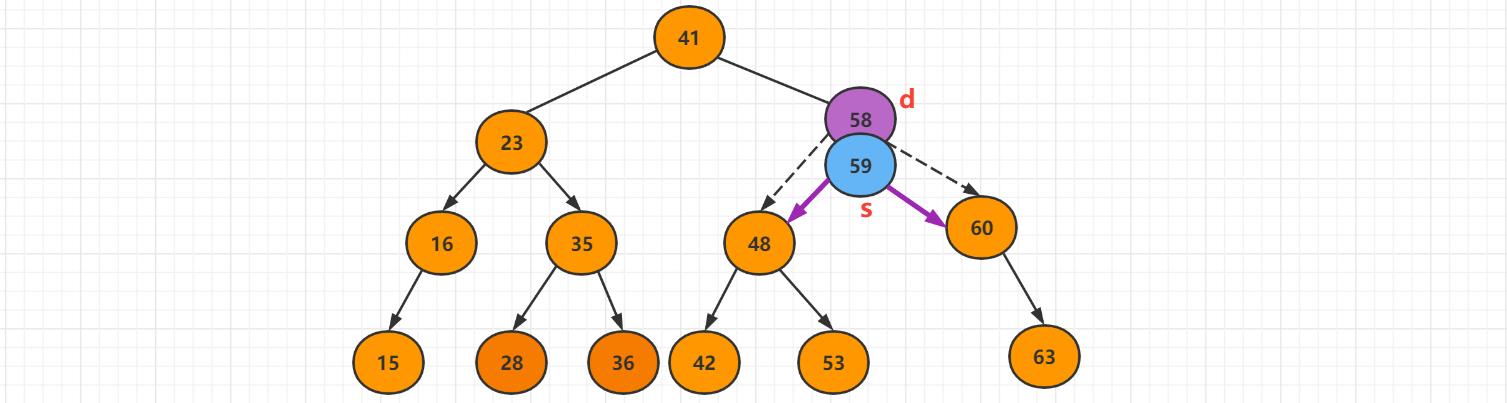
让S的右子树等于被删除节点的右子树,s->right = removeMin(d->right)。
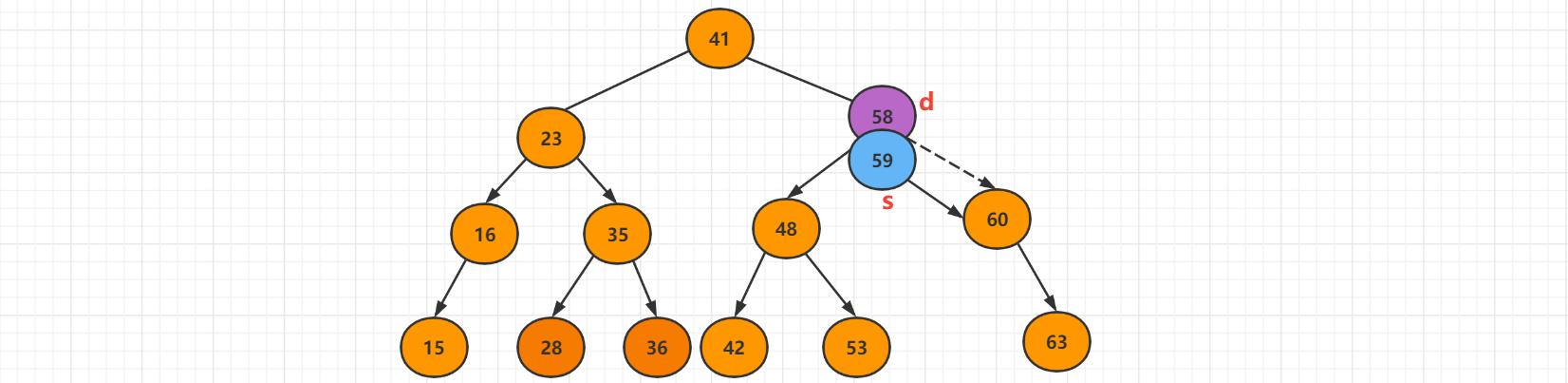
最后让s的左子树等价于d的左子树,最后删除d,S是新的子树的根,s->left = d->left。
1.5 深度优先遍历
深度优先遍历主要包括:先序遍历,中序遍历,后序遍历
1、先序遍历
规则是若二叉树为空,则空操作返回,否则先访问根节点,然后前序遍历左子树,再前序遍历右子树。
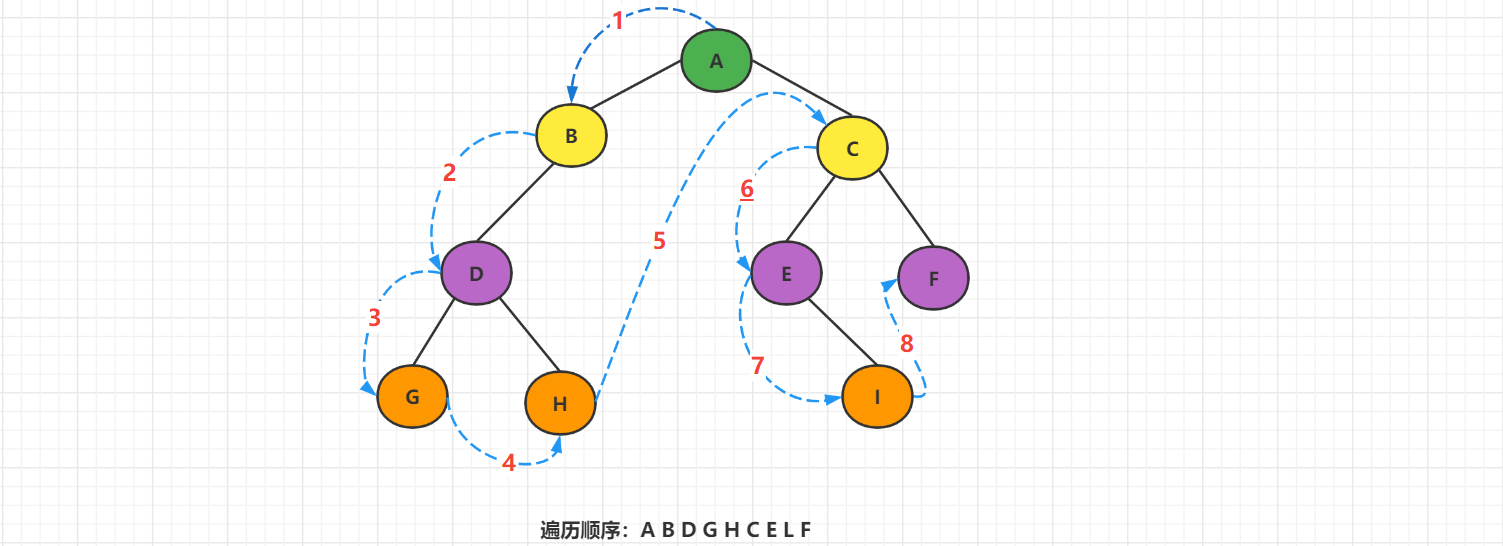
2、中序遍历
规则是若树为空,则空操作返回,否则从根节点开始【注意并不是先访问根节点】,中序遍历根结点的左子树,然后是访问根结点,最后中序遍历右子树。
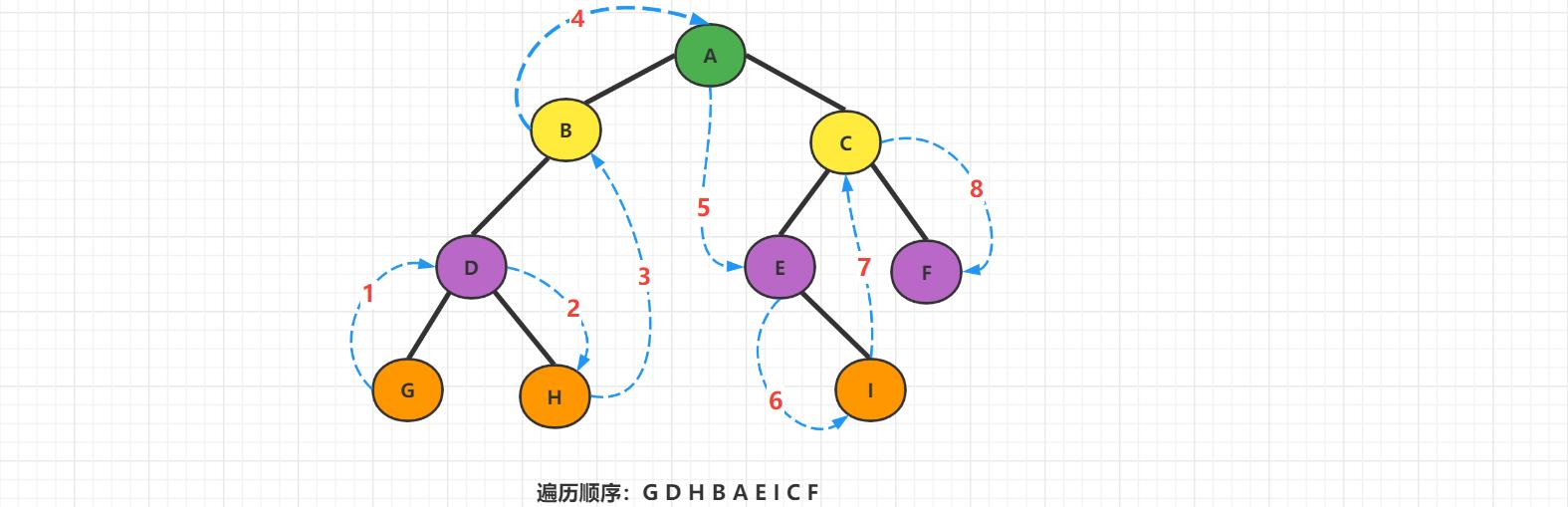
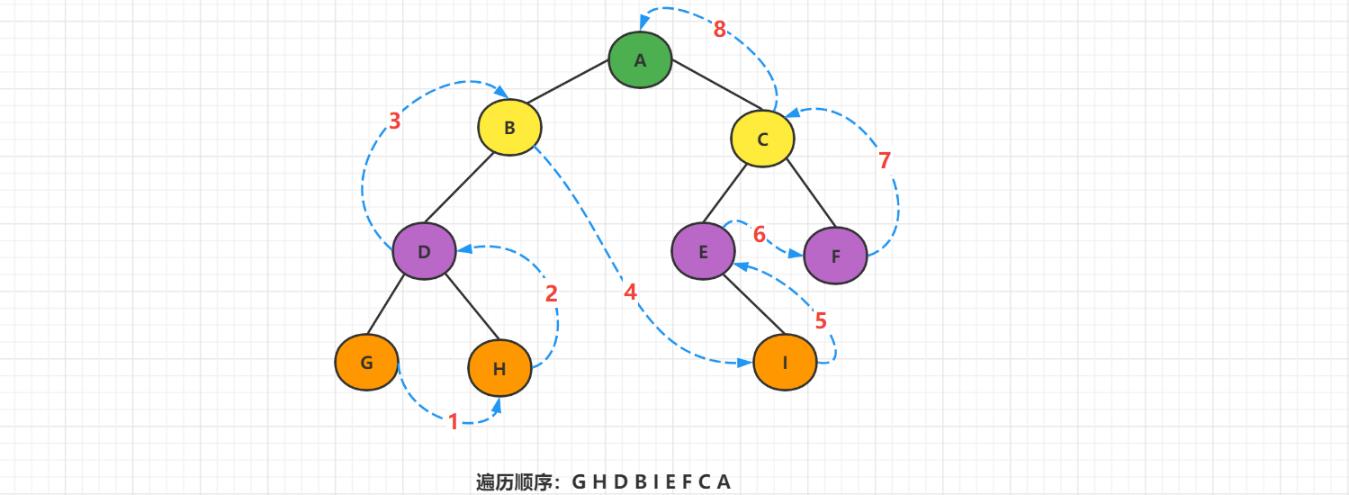
3、后序遍历
规则是若树为空,则空操作返回,否则从根结点开始,后序遍历根节点的左子树,然后后序遍历右子树,最后访问根节点。
1.6 广度优先遍历
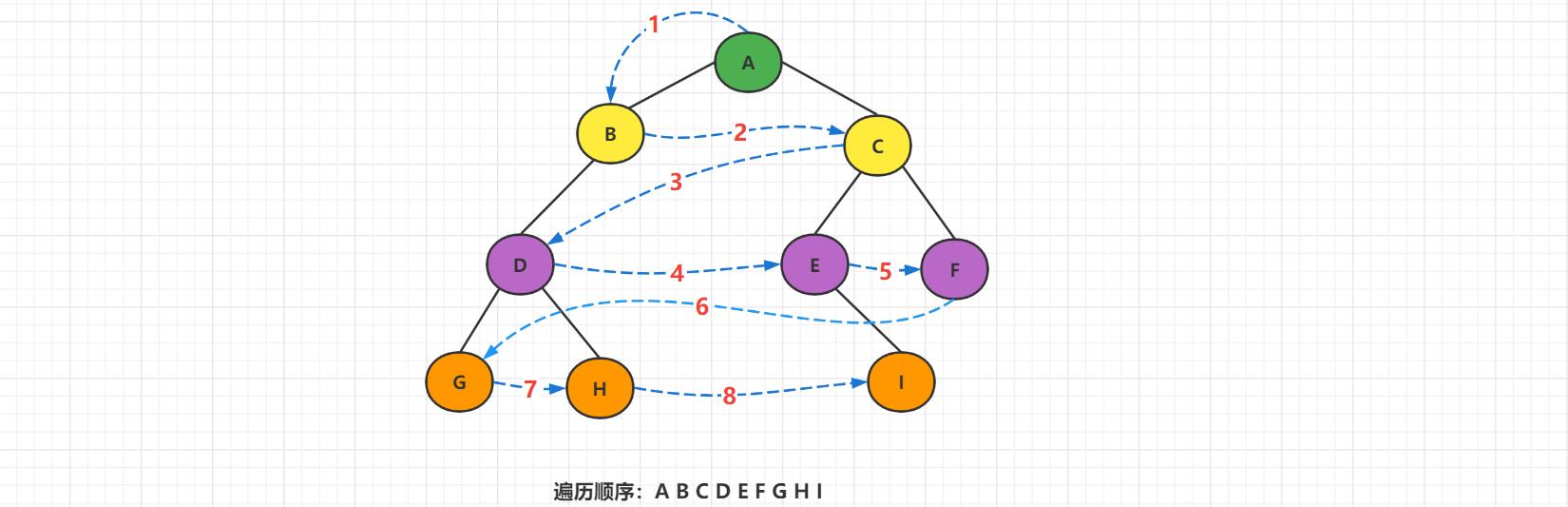
1、层序遍历
规则是若树为空,则空操作返回,否则从树的第一层,也就是根结点开始访问,从上而下逐层遍历,在同一层中,按从左到右的顺序对结点逐个访问。
1.7 代码实现
接口类:List
package cn.binarysearch.demo;
public interface List<E> extends Iterable<E>
void add(E element);
void add(int index, E element) ;
void remove(E element);
E remove(int index);
E get(int index);
E set(int index, E element) ;
int size();
int indexOf(E element) ;
boolean contains(E element);
boolean isEmpty();
void clear();
链表类实现:LinkedList
package cn.binarysearch.demo;
import cn.set.demo.List;
import java.util.Iterator;
// 链表
public class LinkedList<E> implements List<E>
// 创建Node节点
private class Node
// 数据域
E data;
// 指向直接前驱的指针
Node prev;
// 指向直接后继的指针
Node next;
// 构造函数
public Node()
this(null, null, null);
public Node(E data)
this(data, null, null);
public Node(E data, Node prev, Node next)
this.data = data;
this.prev = prev;
this.next = next;
@Override
public String toString()
StringBuilder sb = new StringBuilder();
if (prev != null)
sb.append(prev.data);
else
sb.append("null");
sb.append("->").append(data).append("->");
if (next != null)
sb.append(next.data);
else
sb.append("null");
return sb.toString();
// 链表元素的数量
private int size;
// 声明头结点
private Node head;
// 声明尾节点
private Node tail;
// 初始化头结点
public LinkedList()
head = null;
tail = null;
size = 0;
public LinkedList(E[] arr)
for (E e : arr)
add(e);
//默认向表尾添加元素
@Override
public void add(E element)
add(size, element);
//在链表当中指定索引index处添加一个元素
@Override
public void add(int index, E element)
if (index < 0|| index > size)
throw new ArrayIndexOutOfBoundsException("add index out of bounds");
// 创建新的结点对象
Node node = new Node(element);
// 链表为空
if(isEmpty())
head = node;
tail = node;
tail.next = head;
head.prev = tail;
else if(index == 0) // 在链表头部添加元素
// 头结点的上一跳指向新节点的上一跳
node.prev = head.prev;
node.next = head;
head.prev = node;
head = node;
tail.next = head;
else if(index == size) // 在链表尾部添加元素
node.next = tail.next;
tail.next = node;
node.prev = tail;
tail = node;
head.prev = tail;
else
// 在链表中添加元素
Node p,q; // 定义两个指针变量
if(index <= size / 2)
p = head;
for(int i =0; i < index -1 ; i++)
p = p.next;
q = p.next;
p.next = node;
node.prev = p;
q.prev = node;
node.next = q;
else
p = tail;
for(int i=size -1; i > index; i--)
p = p.prev;
q = p.prev;
q.next = node;
node.prev = q;
p.prev = node;
node.next = p;
size++;
//删除链表中指定的元素element
@Override
public void remove(E element)
int index = indexOf(element);
if(index != -1)
remove(index);
//删除链表中指定角标处index的元素
@Override
public E remove(int index)
if (index < 0|| index > size)
throw new ArrayIndexOutOfBoundsException("remove index out of bounds");
// 定义ret变量
E ret = null;
Node node;
// 当链表只剩一个元素
if(size ==1)
ret = head.data;
head = null;
tail = null;
// 删除表头
else if(index == 0)
ret = head.data;
node = head.next;
head.next = null;
node.prev = head.prev;
head.prev = null;
head = node;
tail.next = head;
// 删除表尾
else if(index == size -1)
ret = tail.data;
node = tail.prev;
tail.prev = null;
node.next = tail.next;
tail.next = null;
tail = node;
head.prev = tail;
else
// 删除链表中间的某一个元素
Node p, q, r;
if(index <= size / 2)
p = head;
for(int i=0; i < index-1; i++)
p = p.next;
q = p.next;
ret = q.data;
r = q.next;
p.next = r;
r.prev = p;
q.next = null;
q.prev = null;
else
p = tail;
for(int i = size -1; i > index + 1; i--)
p = p.prev;
q = p.prev;
ret = q.data;
r = q.prev;
r.next = p;
p.prev = r;
q.next = null;
q.prev = null;
size --;
return ret;
//获取链表中指定索引处的元素
@Override
public E get(int index)
if (index < 0|| index > size)
throw new ArrayIndexOutOfBoundsException("get index out of bounds");
// 获取头
if(index == 0)
return head.data;
else if(index == size -1)
// 获取尾部
return tail.data;
else
// 获取中间
Node p = head;
for (int i = 0; i < index; i++)
p = p.next;
return p.data;
// 修改链表中指定索引index的元素为element
@Override
public E set(int index, E element)
if (index < 0|| index > size)
throw new ArrayIndexOutOfBoundsException("set index out of bounds");
E ret = null;
// 获取头
if(index == 0)
// 修改头
ret = head.data;
head.data = element;
else if(index == size -1)
// 修改尾部元素
ret = tail.data;
tail.data = element;
else
// 修改中间
Node p = head;
for (int i = 0; i < index; i++)
p = p.next;
ret = p.data;
p.data = element;
return ret;
@Override
public int size()
return size;
//查找元素在链表中第一次出现的索引
@Override
public int indexOf(E element)
if(isEmpty())
return -1;
Node p = head;
int index = 0;
while (!p.data.equals(element))
p = p.next;
index++;
if(p == head)
return -1;
return index;
//在链表中判断是否包含元素element
@Override
public boolean contains(E element)
return indexOf(element) != -1;
@Override
public boolean isEmpty()
return size== 0 && head == null && tail == null;
@Override
public void clear()
head = null;
tail = null;
size = 0;
@Override
public String toString()
StringBuilder res = new StringBuilder();
res.append("size=").append(size).append(", [");
Node node = head;
for (int i = 0; i < size; i++)
if (i != 0)
res.append(", ");
res.append(node);
node = node.next;
res.append("]");
return res.toString();
@Override
public Iterator<E> iterator()
return new DoubleCircleLinkedListIterator();
class DoubleCircleLinkedListIterator implements Iterator<E>
private Node cur = head;
private boolean flag = true;
@Override
public boolean hasNext()
if(isEmpty())
return false;
return flag;
@Override
public E next()
E ret = cur.data;
cur = cur.next;
if(cur == head)
flag = false;
return ret;
二分搜索树实现:BinarySearchTree
package cn.binarysearch.demo;
import java.util.Iterator以上是关于二分搜索树实现的主要内容,如果未能解决你的问题,请参考以下文章