二十 二分搜索树完整实现:查找删除操作
Posted ltfxy
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了二十 二分搜索树完整实现:查找删除操作相关的知识,希望对你有一定的参考价值。
二分搜索树删除元素的逻辑:
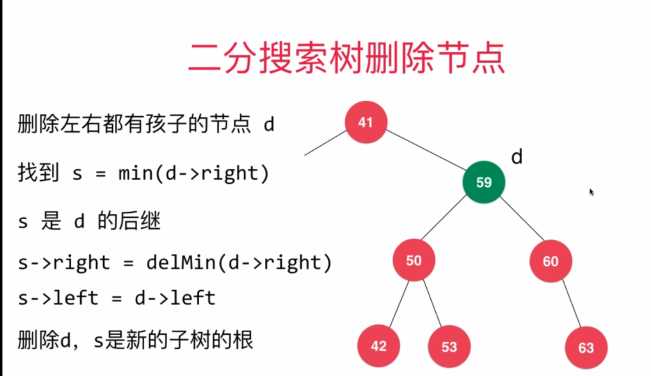
二分搜索树的完整实现:
package com.lt.datastructure.BST; import java.util.LinkedList; import java.util.Queue; import java.util.Stack; public class BST<E extends Comparable<E>> { private class Node{ public E e; Node left,right; public Node(E e) { this.e = e; this.left = left; this.right = right; } } private Node root; private int size; public BST(){ root = null; size = 0; } public int size() { return size; } public boolean isEmpty(){ return size==0; } /* * 二分搜索树添加元素 * 小于根结点,添加到左边,大于则添加到右边,等于根节点,则不作任何改变,二分搜索树不包含重复元素 * */ public void add(E e){ //如果根节点为空 if(root == null){ root = new Node(e); size ++; }else{ add(root,e); } } //向以root为根的二分搜索树中插入元素E,递归算法 private Node add(Node node , E e){ /* //元素重复,不做操作 if(e.equals(node.e)){ return; } //小于根节点,而左子树为空,添加到左子树 else if(e.compareTo(node.e)<0 && node.left==null){ node.left = new Node(e); size ++; return; } //大于根节点而右子树为空,添加到右子树 else if(e.compareTo(node.e)>0 && node.right==null){ node.right = new Node(e); size ++; return; } //根节点的左右子树不为空,调用递归,直到找到孩子为空的情况 if(e.compareTo(node.e)<0){ add(node.left,e); }else{ add(node.right,e); } */ //递归的出口,找到子树为null,则必然添加,完成操作 if(node == null){ size++; return new Node(e); } if(e.compareTo(node.e)<0){ //如果左子树为null,则node.left = new Node(e);如果不为空,继续递归 node.left = add(node.left,e); } else if(e.compareTo(node.e)>0){ ////如果右子树为null,则node.right = new Node(e);如果不为空,继续递归 node.right = add(node.right,e); } //其他情况,比如元素相等,则返回传进来的根节点,不做操作 return node; } //查询二分搜索树中是否包含元素e public boolean contains(E e){ return contains(root,e); } //看以node为根的二分搜索树中是否含有元素e,递归实现 private boolean contains(Node node , E e){ if(node == null){ return false; } if(e.compareTo(node.e)==0){ return true; } else if(e.compareTo(node.e)<0){ return contains(node.left,e); }else{ return contains(node.right,e); } } //查找二分搜索树的最小元素 public E minimum(){ if(size==0) throw new IllegalArgumentException("BST is Empty"); return minimum(root).e; } private Node minimum(Node node) { //递归终点:node.ledt==null,递归调用: return minimum(node.left) return node.left==null ? node:minimum(node.left); } //查找二分搜索树的最大元素 public E maximum(){ if(size==0) throw new IllegalArgumentException("BST is Empty"); return maximum(root).e; } private Node maximum(Node node) { return node.right == null ? node : maximum(node.right); } //删除二分搜索树的最小值并返回 public E removeMin(){ E ret = minimum(); //改变最小值所对应的根节点,达到删除的目的 root = removeMin(root); return ret; } //删除掉以node为根的二分搜索树的最小节点 //返回删除结点后新的二分搜索树的根,根节点依然为node private Node removeMin(Node node) { //递归终点,node.left==null if(node.left == null){ //如果有右子树,将其保存,如果没有,返回null Node rightNode = node.right; node.right = null; size--; return rightNode; } //假如node.left.e是最小值,node.left = node.left.right //right为空,则最小值为空,right不为空,则原结点最小值删除,右子树对接保留 node.left = removeMin(node.left); return node; } //删除二分搜索树的最大值 public E removeMax(){ E ret = maximum(root).e; //改变最小值所在根节点,达到删除的目的 root = removeMax(root); return ret; } private Node removeMax(Node node) { //递归终点 if(node.right==null){ Node leftNode = node.left; node.right = null; size--; return leftNode; } //递归调用 node.right = removeMax(node.right); return node; } /* * 删除二叉树的结点: * 待删除结点右子树为空:将此结点的左子树取代它的位置 * 待删除结点左子树为空:将此结点的右子树取代它的位置 * 待删除结点左右子树都不为空: * 1 找到比待删除结点大的最小节点:即待删除结点右子树的最小值minimum(node.r)取代它的位置 * 1 找到比待删除结点小的最大节点:即待删除结点右子树的最小值maximum(node.r)取代它的位置 */ public void remove(E e){ //删除以root为根结点中值为e的元素,删完之后赋给root root = remove(root,e); } private Node remove(Node node, E e) { //递归终点 if(node == null){ return null; } //查找e相对于root的位置, if(e.compareTo(node.e)<0){ //如果在左边,则继续往左深度查找,直到找到或者null //因为递归到null(结点不存在)或者删除(结点也不存在)才停止,所以返回的是上一个结点node node.left = remove(node.left,e); return node; } else if(e.compareTo(node.e)>0){ //如果在右边,则往右深度查找,直到找到或者null node.right = remove(node.right,e); return node; } else{//e.compareTo(node.e)=0 //此时已找到 //如果该结点左右子树都为空,则参考1、2情况皆可 //1 如果该结点的左子树为空,则删除该结点,使其指向原来的右子树 if(node.left == null){ Node rightNode = node.right; node.right = null; size--; return rightNode;//rightNode替代待删除结点:node.x=rightNode; return node; } //2如果该结点的右子树为空,则删除该结点,使其指向原来的左子树 if(node.right == null){ Node leftNode = node.left; node.left = null; size --; return leftNode; } //3 如果左右结点都不为空,找到大于且最接近此节点的结点,即该结点右子树的最小值minimum(node.r) Node successor = minimum(node.right); //此结点的右子树由原来的右子树(需要剔原来右子树里的此结点)接上 successor.right = removeMin(node.right); //此节点的左子树由原来的左子树接上 successor.left = node.left; //删除原来的树 node.left = null; node.right = null; return successor; //successor替代了待删除结点 } } /* * 二分搜索树的前序遍历(先访问结点,再访问左,右子树),最自然,最常用的遍历方式 * * */ public void preOrder(){ preOrder(root); } private void preOrder(Node node){ //递归终止 if(node==null){ return; } //递归调用 System.out.println(node.e);//首先打印根节点 preOrder(node.left);//然后递归left,直到left为空,回溯,打印left由深到浅 preOrder(node.right);//最后递归完了left,递归right,right打印由浅到深 } /* * 二分搜索树的中序遍历(访问左子树,结点,右子树),顺序由小到大,最自然,最常用的遍历方式 * */ public void inOrder(){ inOrder(root); } //中序遍历以node为根的二分搜索树,递归算法 private void inOrder(Node node){ if(node==null){ return; } inOrder(node.left);//由深到浅打印left System.out.println(node.e);//每递归一次,打印当前根节点 inOrder(node.right);//由浅到深打印right } /* * 二分搜索树的后序遍历(访问右子树,左子树,结点),最自然,最常用的遍历方式 * */ public void postOrder(){ postOrder(root); } private void postOrder(Node node) { //递归的终点 if(node == null){ return; } postOrder(node.left);//打印right由深到浅 postOrder(node.right);//打印left由深到浅 System.out.println(node.e);//最后打印根节点 } /* * 先序中序后序遍历的打印特点: * 对于每个结点,都有三次访问,可以用三个点代表三次操作。 * 先序遍历:打印发生在第一此访问。 * 中序遍历:打印发生在第二次访问。 * 后序遍历:打印发生在第三次访问。 */ /* * 非递归的前序遍历,栈实现 * 将根节点入栈,定义cur接收出栈结点 * 当栈不为null,则打印cur.e * 因为先进后出,所以依次入栈cur的右子树,左子树,出栈、打印栈的左子树,右子树 */ public void inOrderNR(){ Stack<Node> stack = new Stack<>(); stack.push(root); while(!stack.isEmpty()){ Node cur = stack.pop(); System.out.println(cur.e); if(cur.right!=null){ stack.push(cur.right); } if(cur.left!=null){ stack.push(cur.left); } } } /* * 二分搜索树的层序遍历(广度优先遍历),队列实现 * 广度优先遍历优势在于更快找到想要查询的元素,主要用于搜索策略,算法设计--最短路径(无权图) */ public void levelOrder(){ Queue<Node> q = new LinkedList<>(); q.add(root); while(!q.isEmpty()){ Node cur = q.remove(); System.out.println(cur.e); if(cur.left!=null){ q.add(cur.left); } if(cur.right!=null){ q.add(cur.right); } } } //遍历的展示 @Override public String toString() { StringBuilder res = new StringBuilder(); BSTString(root,0,res); return res.toString(); } //生成以node为根节点,深度为depth描述的字符串 private void BSTString(Node node, int depth, StringBuilder res) { if(node==null){ res.append(DepthString(depth)+"null "); return; } res.append(DepthString(depth)+node.e+" "); BSTString(node.left,depth+1,res); BSTString(node.right, depth+1, res); } private String DepthString(int depth) { StringBuilder res = new StringBuilder(); for(int i=0; i<depth ; i++){ res.append("--"); } return res.toString(); } }
测试:
查找最大值最小值:
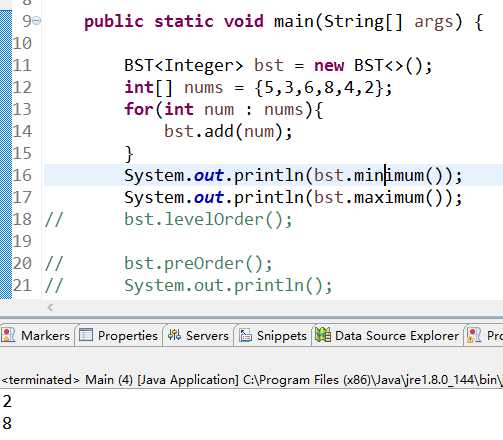
删除最小值:
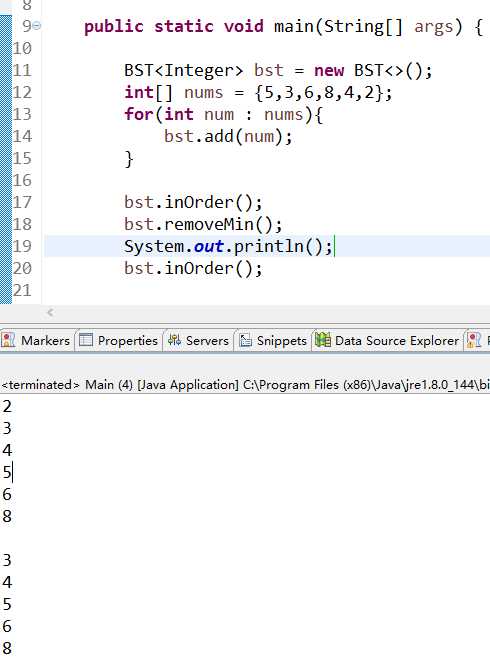
删除最大值:
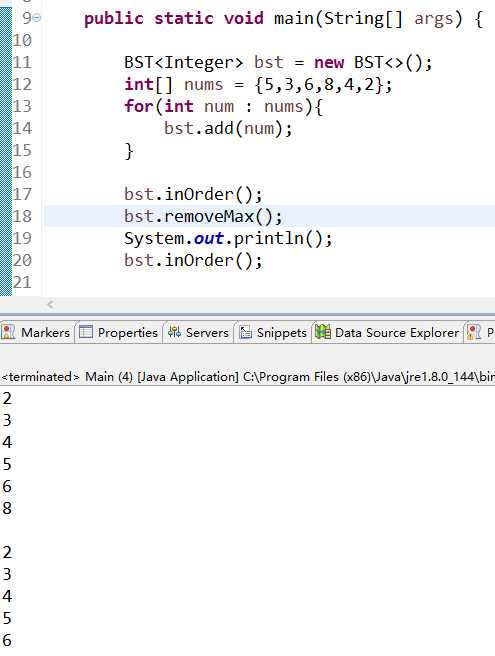
以上是关于二十 二分搜索树完整实现:查找删除操作的主要内容,如果未能解决你的问题,请参考以下文章