算法给小码农八大排序 八奇计只为宝儿姐
Posted 小码农UU
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了算法给小码农八大排序 八奇计只为宝儿姐相关的知识,希望对你有一定的参考价值。

八排 八奇迹
排序
排序的概念及其运用
排序的概念
==排序:==所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
==稳定性:==假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
==内部排序:==数据元素全部放在内存中的排序。
==外部排序:==数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
排序运用
来上京东
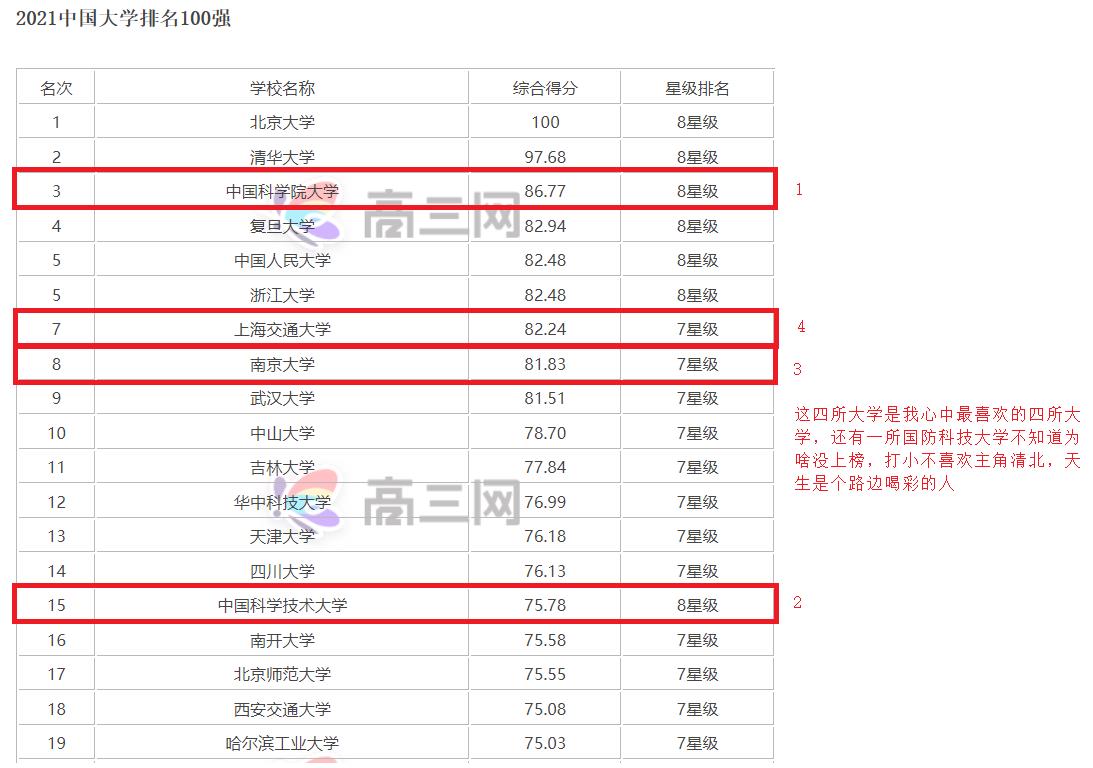
大学排名
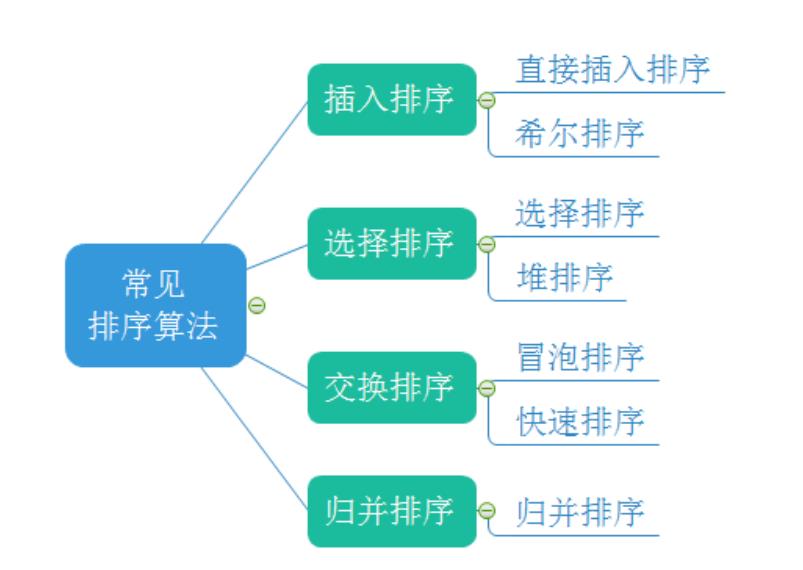
常见的排序算法
常见排序算法的实现
插入排序
基本思想
直接插入排序是一种简单的插入排序法,其基本思想是:把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。
实际中我们玩扑克牌时,就用了插入排序的思想



但是数组肯定不是有序的,所以我们得先让数组有序
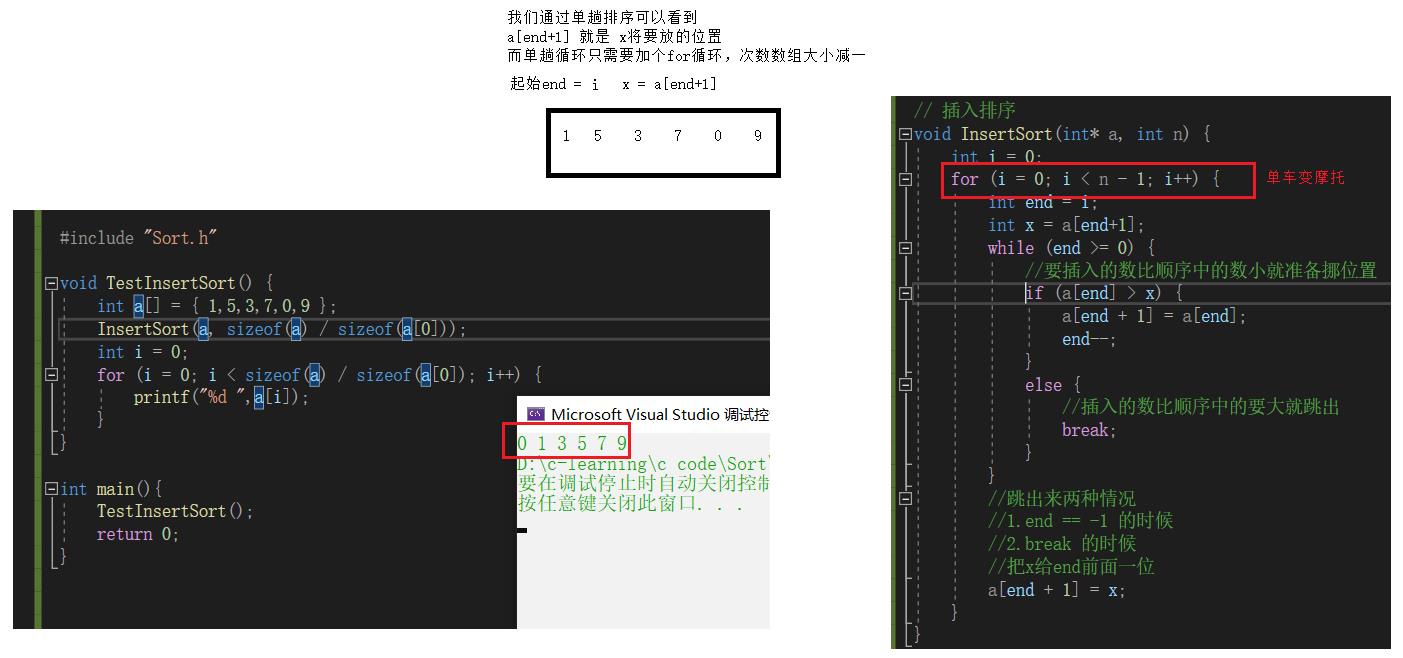
先把打印数组给剥离出来
// 打印数组
void PrintArray(int* a, int n)
assert(a);
int i = 0;
for (i = 0; i < n; i++)
printf("%d ", a[i]);
printf("\\n");
插入排序
// 插入排序
void InsertSort(int* a, int n)
assert(a);
int i = 0;
for (i = 0; i < n - 1; i++)
int end = i;
int x = a[end+1];
while (end >= 0)
//要插入的数比顺序中的数小就准备挪位置
if (a[end] > x)
a[end + 1] = a[end];
end--;
else
//插入的数比顺序中的要大就跳出
break;
//跳出来两种情况
//1.end == -1 的时候
//2.break 的时候
//把x给end前面一位
a[end + 1] = x;
插入排序的时间复杂度:O(N2)
最好:O(N) — 顺序有序 (接近有序)
最坏:O(N2) — 逆序
插入排序的空间复杂度:O(1)
希尔排序( 缩小增量排序 ) (反正希尔牛逼)
希尔排序是在优化直接插入排序,而且效果超级明显,为什么是优化呢,因为我们知道直接插入排序接近有序了就会非常快,那我就创造这样的有序,让他时间复杂度接近O(N),我们知道排序的时间复杂度最好情况就是O(N),而我们接近O(N)也是相当了不起了,基本是接近天花板了
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个整数,把待排序文件中所有记录分成个组,所有距离为的记录分在同一组内,并对每一组内的记录进行排序。然后,取,重复上述分组和排序的工作。当到达=1时,所有记录在统一组内排好序。
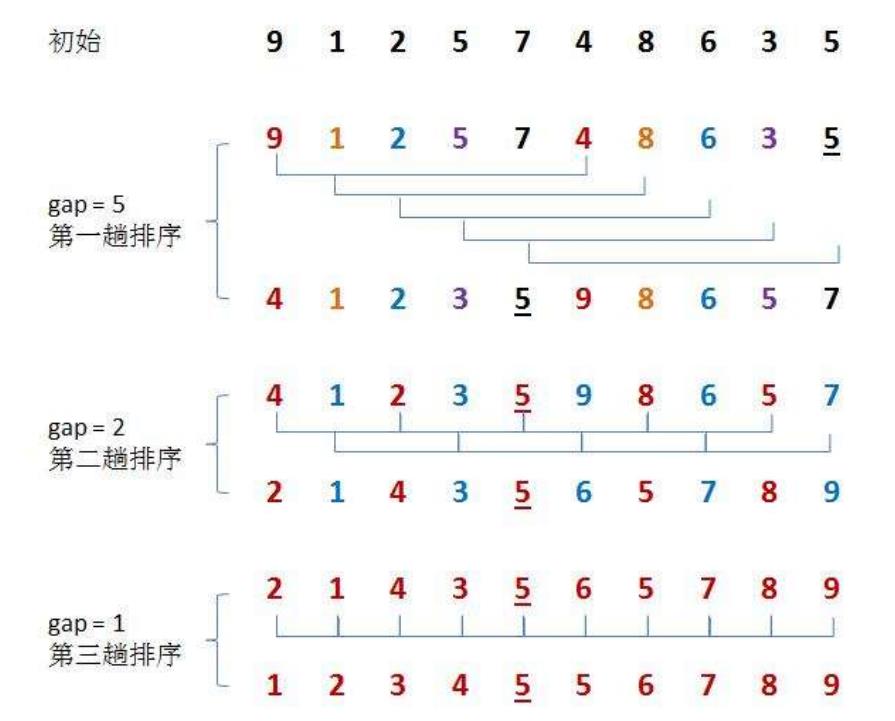
希尔排序步骤
1.分组预排序 ---- 数组接近有序
按gap分组,对分组值进行插入排序 分成gap组
2.直接插入排序 数组接近有序,直接插入的时间复杂度就是O(N)
单组多躺
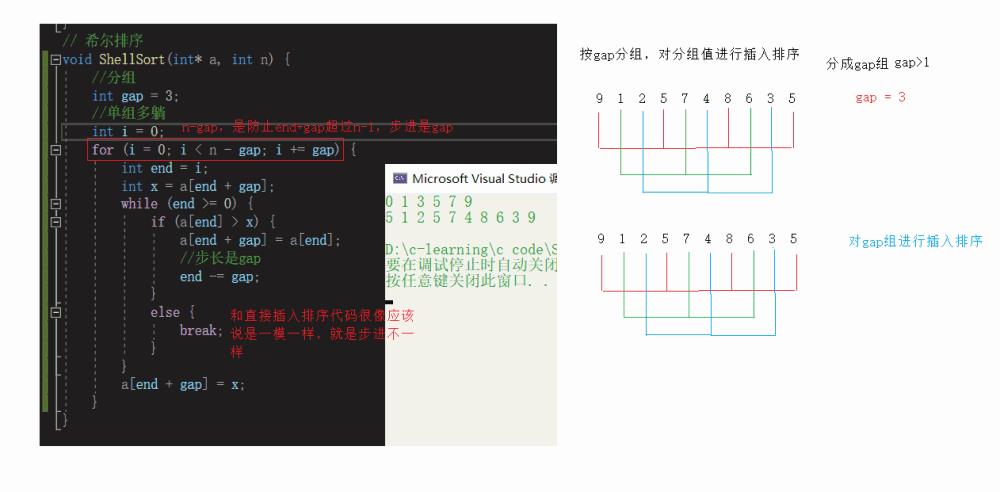
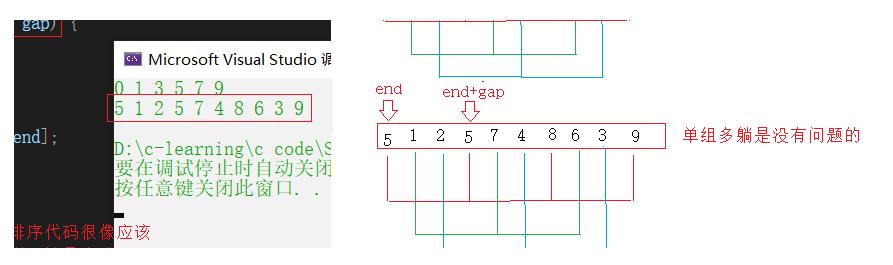
多组插入
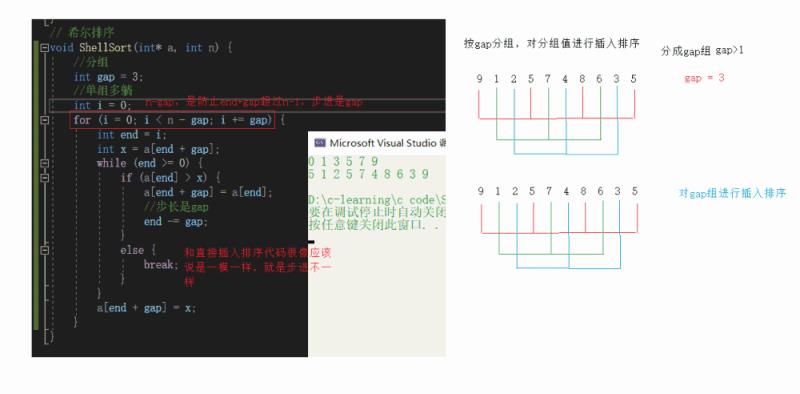
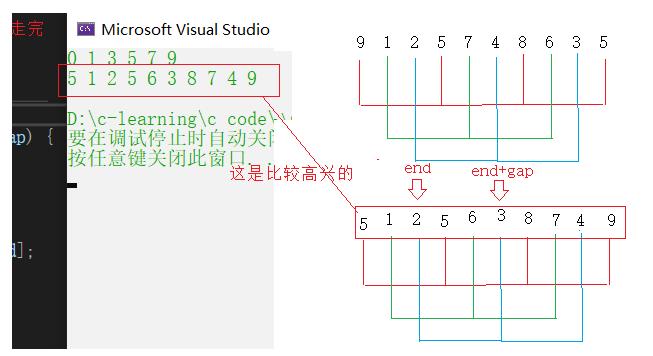
间距为gap多组预排实现的时间复杂度O(gap*(1+…+N/gap))
最好:O(N)
最好:O(N)
最坏:O(gap*(1+…+N/gap))
gap越大,预排越快,预排后越不接近有序
gap越小,预排越慢,预排后越接近有序
多组一锅炖(要是分组插麻烦我们也可以一锅炖)
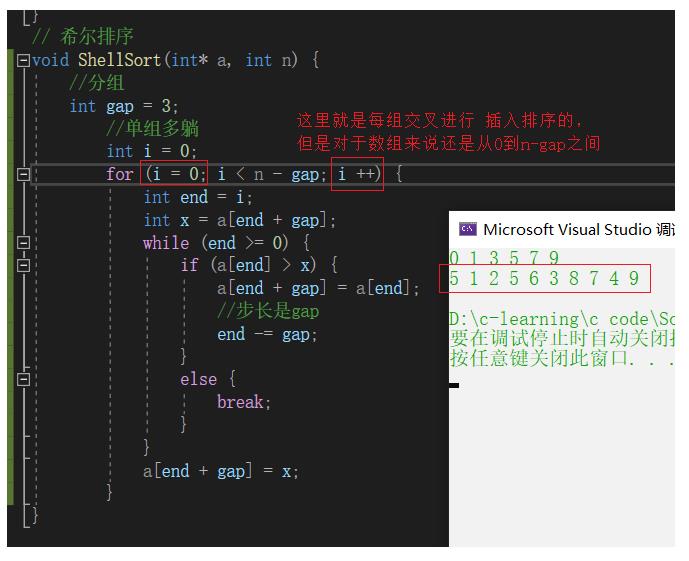
多次预排序(gap > 1)+直接插入(gap == 1)
gap/2
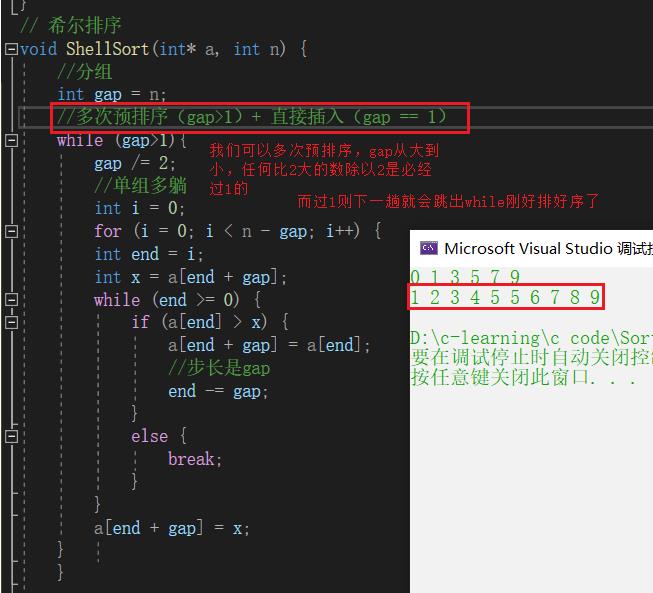
gap/3
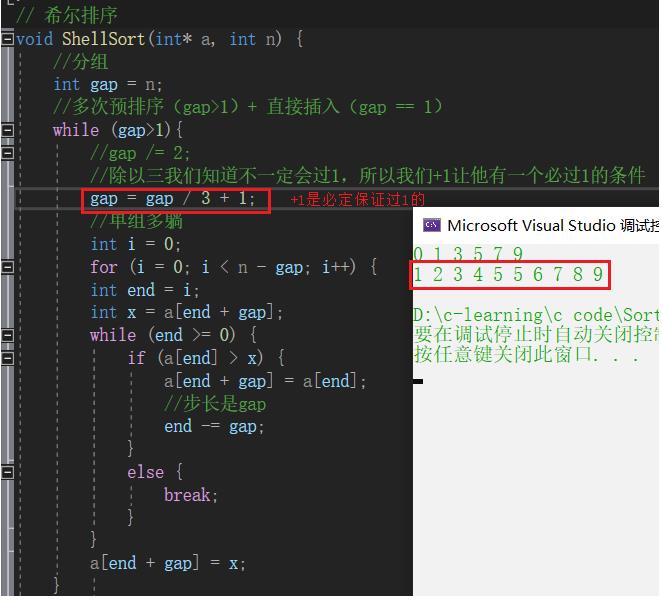
时间复杂度O(N1.3)记住就行,反正记住希尔很牛逼就行,希尔排序很快
测直接插入排序和希尔排序的性能(让你看看什么才叫希尔排序)

堆
数据结构中的堆不同于操作系统中的堆(操作系统中的堆是用来存储动态内存的),数据结构中的堆是数据的存储方式。数据结构中的堆是完全二叉树
既然堆是完全二叉树的形式存储的那么就非常适合用数组的方式来表示
堆的概念及结构
如果有一个关键码的集合K = k0,k1, k2,…,kn-1,把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足:Ki <= K2i+1 且 Ki<= K2i+2 (Ki >= K2i+1 且 Ki >= K2i+2) i = 0,1,2…,则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
大堆:树中一个树及子树中,任何一个父亲都大于等于孩子
小堆:树中一个树及子树中,任何一个父亲都小于等于孩子
堆的性质
堆中某个节点的值总是不大于或不小于其父节点的值;
堆总是一棵完全二叉树。**
堆的结构(这里实现大堆)
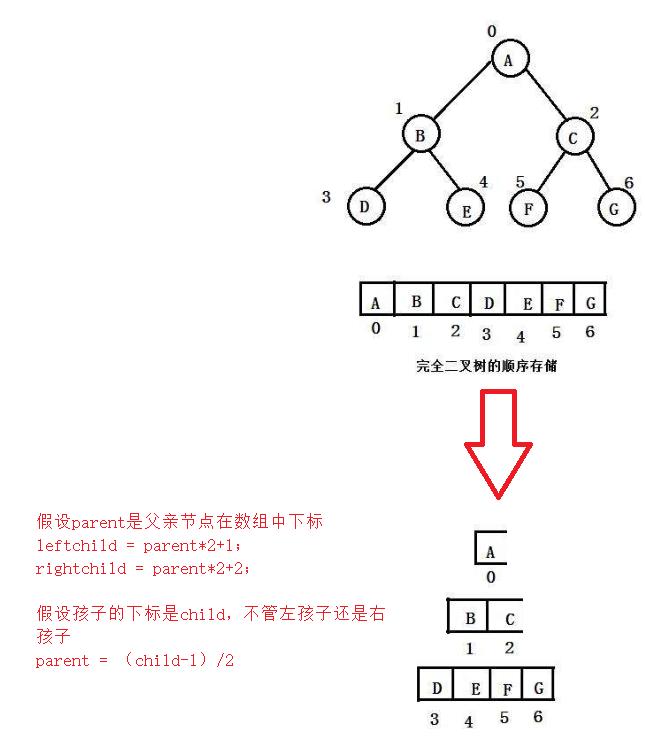
既然还是数组的结构的话就还是顺序表的处理方式,数组指针,size,capacity。虽然物理上我们是用顺序表的方式来表示,但是他实际上表示的数据是完全二叉树。
堆的结构体
typedef int HPDataType;
typedef struct Heap
HPDataType* a;
int size;
int capacity;
HP;
堆初始化函数HeapInit
就是一个指向NULL的数组,size 和 capacity都为零
//堆初始化函数
void HeapInit(HP* hp)
assert(hp);
hp->a = NULL;
hp->size = hp->capacity = 0;
堆销毁函数HeapDestroy
由于数组是动态开辟的,所以用完后需要销毁的,不然会内存泄漏
//堆销毁函数
void HeapDestroy(HP* hp)
assert(hp);
free(hp->a);
hp->size = hp->capacity = 0;
堆打印函数HeapPrint
可以想象成一种快速调试,类似于单片机中的串口打印看数据收发情况
//堆打印函数
void HeapPrint(HP* hp)
int i = 0;
for (i = 0; i < hp->size; i++)
printf("%d ", hp->a[i]);
printf("\\n");
向上调整函数AdjustUp
为了不影响数据的存储形式(大堆还得是大堆),插入数据就不能破坏大堆的形式,我们需要把堆插入函数中的数据调整给剥离出来
我们可以看到插入的这个数据对其他的节点并没有什么影响,有影响的只是这个节点到根这条路径上的节点,如何解决对这条路径的影响呢,我们可以形象的看到仅仅是在这条路径上进行向上调整
通过parent = (child-1)/2 找到父亲节点,与之进行比较,然后父亲小就交换位置(大堆),然后交换后就在找上面的父亲节点,直到找到父亲大于孩子,就不交换了

//向上调整函数
void AdjustUp(HPDataType* a, int child)
assert(a);
int parent = (child - 1) / 2;
while (child>0)
if (a[parent] < a[child])//父亲小于孩子就交换(大堆)
a[parent] = a[parent] ^ a[child];
a[child] = a[parent] ^ a[child];
a[parent] = a[parent] ^ a[child];
//交换好后重新称呼一下孩子与父亲
child = parent;
parent = (child - 1) / 2;
else
break;
堆插入函数HeapPush


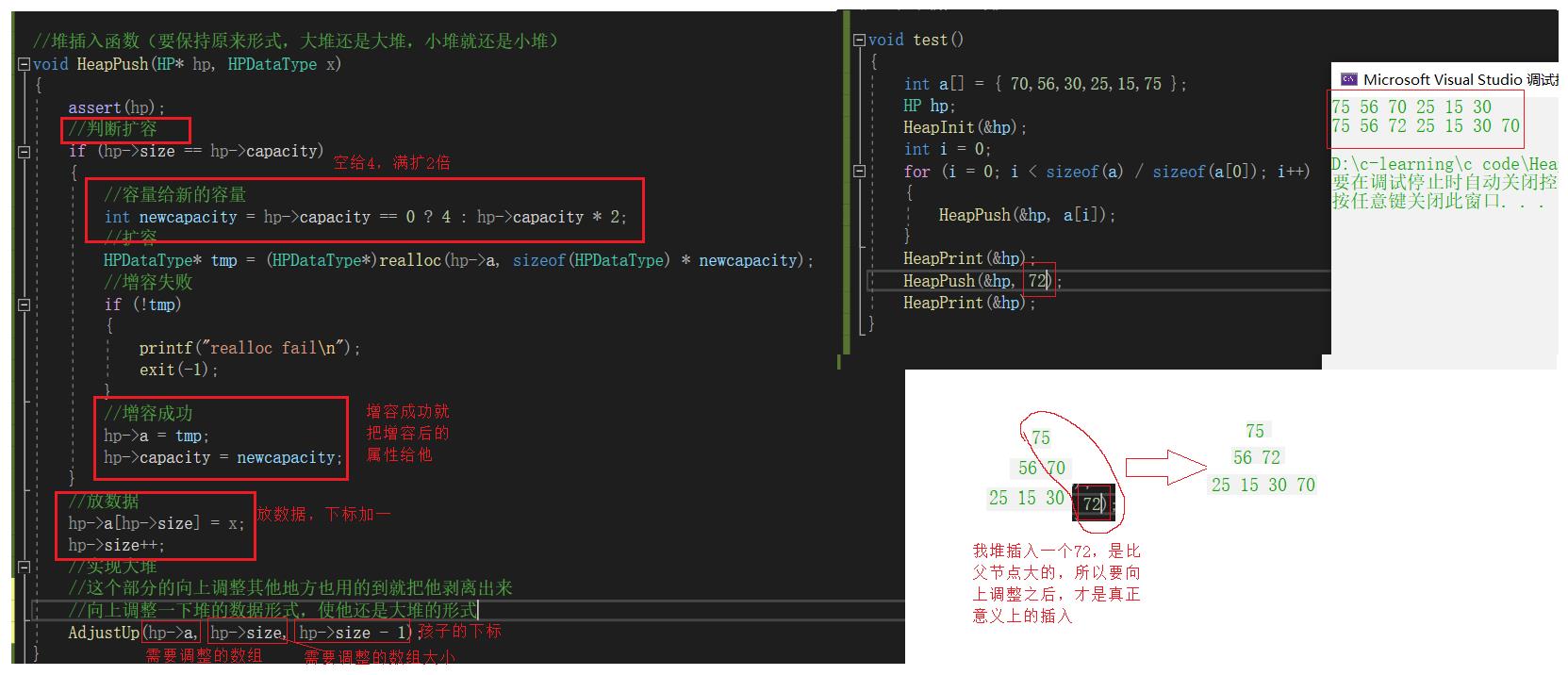
//堆插入函数(要保持原来形式,大堆还是大堆,小堆就还是小堆)
void HeapPush(HP* hp, HPDataType x)
assert(hp);
//判断扩容
if (hp->size == hp->capacity)
//容量给新的容量
int newcapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;
//扩容
HPDataType* tmp = (HPDataType*)realloc(hp->a, sizeof(HPDataType) * newcapacity);
//增容失败
if (!tmp)
printf("realloc fail\\n");
exit(-1);
//增容成功
hp->a = tmp;
hp->capacity = newcapacity;
//放数据
hp->a[hp->size] = x;
hp->size++;
//实现大堆
//这个部分的向上调整其他地方也用的到就把他剥离出来
AdjustUp(hp->a, hp->size - 1);//child下标
判断堆是否为空函数HeapErmpy
//判断堆是否为空函数
bool HeapErmpy(HP* hp)
assert(hp);
return hp->size == 0;
返回堆大小函数HeapSize
//返回堆大小函数
int HeapSize(HP* hp)
assert(hp);
return hp->size;
下面还会用到交换函数,上面也有那么我们不妨把他剥离出来封装一下,就不需要重复写了
交换函数Swap
//交换函数void Swap(HPDataType* px, HPDataType* py) *px = *px ^ *py; *py = *px ^ *py; *px = *px ^ *py;
向下调整函数AdjustDown
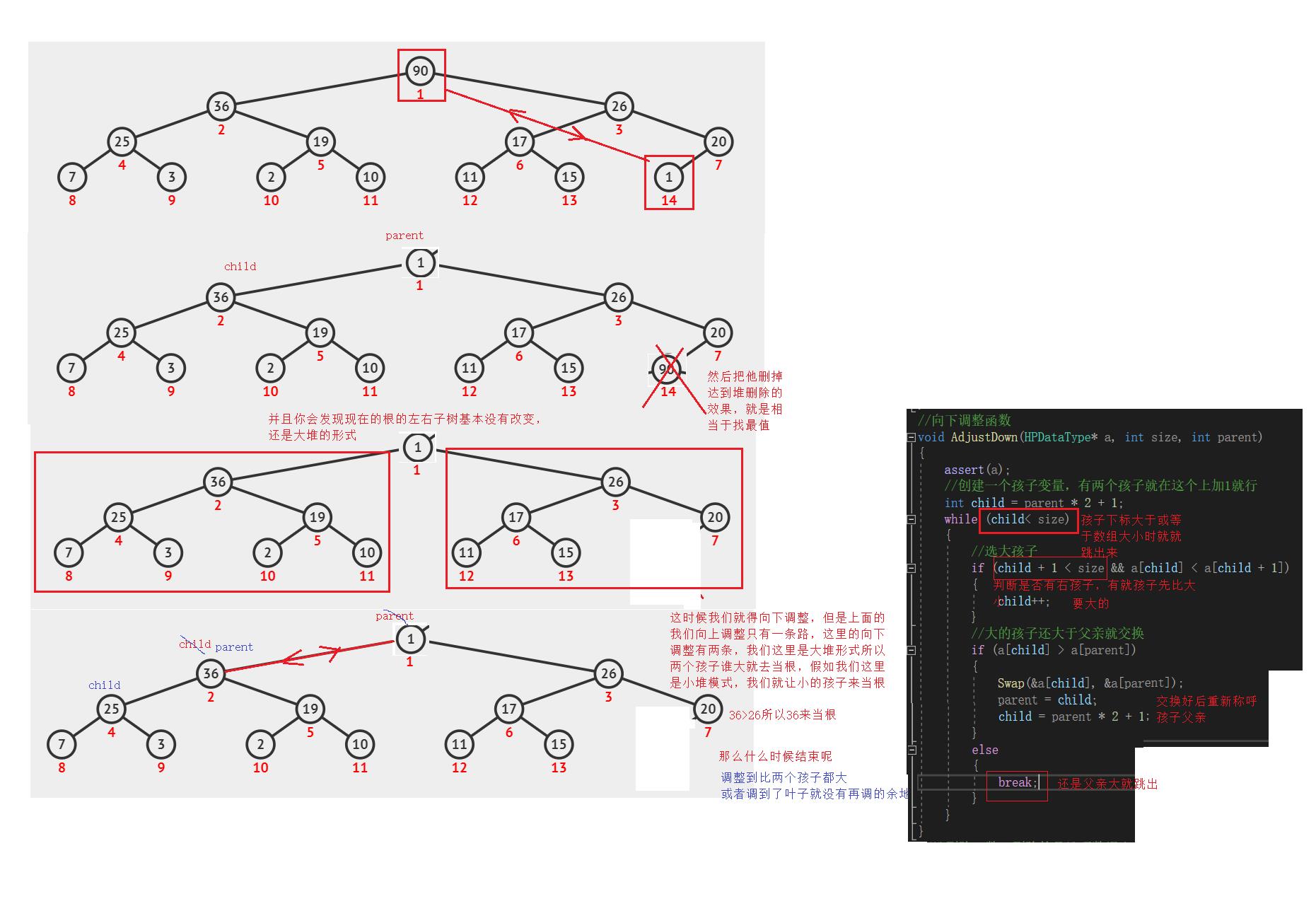
//向下调整函数void AdjustDown(HPDataType* a, int size, int parent) assert(a); //创建一个孩子变量,有两个孩子就在这个上加1就行 int child = parent * 2 + 1; while (child< size) //选大孩子 if (child + 1 < size && a[child] < a[child + 1]) child++; //大的孩子还大于父亲就交换 if (a[child] > a[parent]) Swap(&a[child], &a[parent]); parent = child; child = parent * 2 + 1;
堆删除函数HeapPop

我们可以认为假想根和堆的最后一个元素交换后,把最后一个删除,然后再对堆进行操作,你会发现,我们没有破坏原来的整体结构
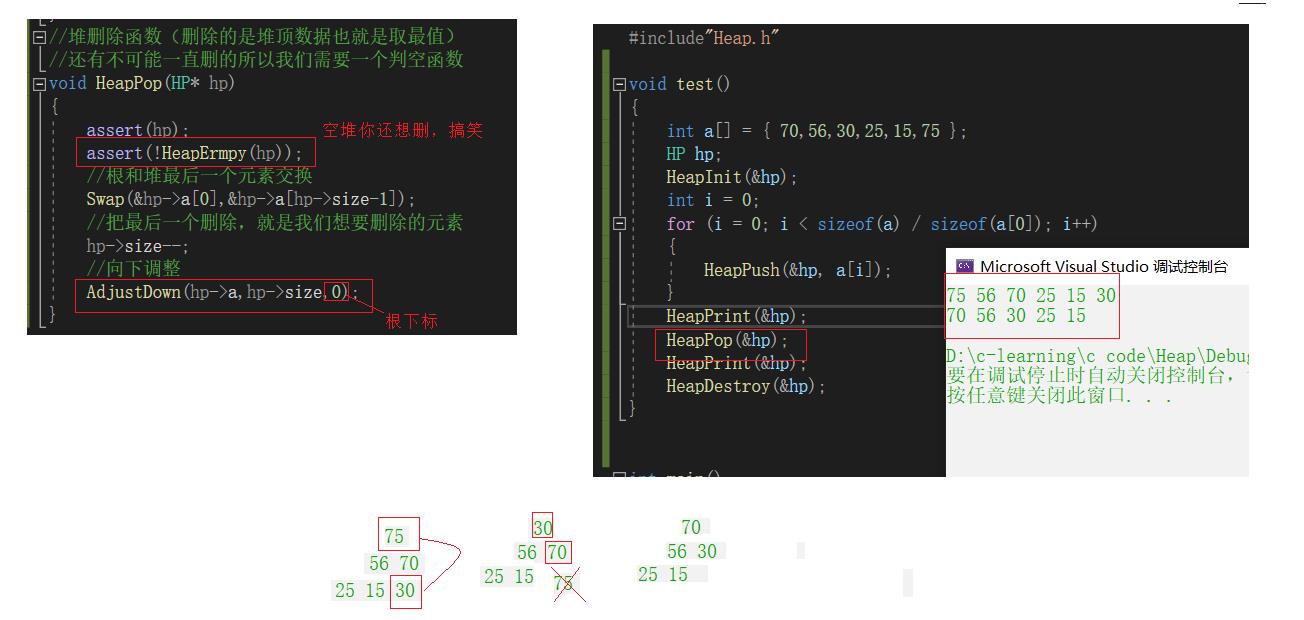
//堆删除函数(删除的是堆顶数据也就是取最值)
//还有不可能一直删的所以我们需要一个判空函数
void HeapPop(HP* hp)
assert(hp);
assert(!HeapErmpy(hp));
//根和堆最后一个元素交换
Swap(&hp->a[0],&hp->a[hp->size-1]);
//把最后一个删除,就是我们想要删除的元素
hp->size--;
//向下调整
AdjustDown(hp->a,hp->size,0);
排序
常见的排序算法

常见排序算法的实现
选择排序 最慢排序(最好理解)所以搬血
基本思想:
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。
直接选择排序
在元素集合array[i]–array[n-1]中选择关键码最大(小)的数据元素
若它不是这组元素中的最后一个(第一个)元素,则将它与这组元素中的最后一个(第一个)元素交换
在剩余的array[i]–array[n-2](array[i+1]–array[n-1])集合中,重复上述步骤,直到集合剩余1个元素
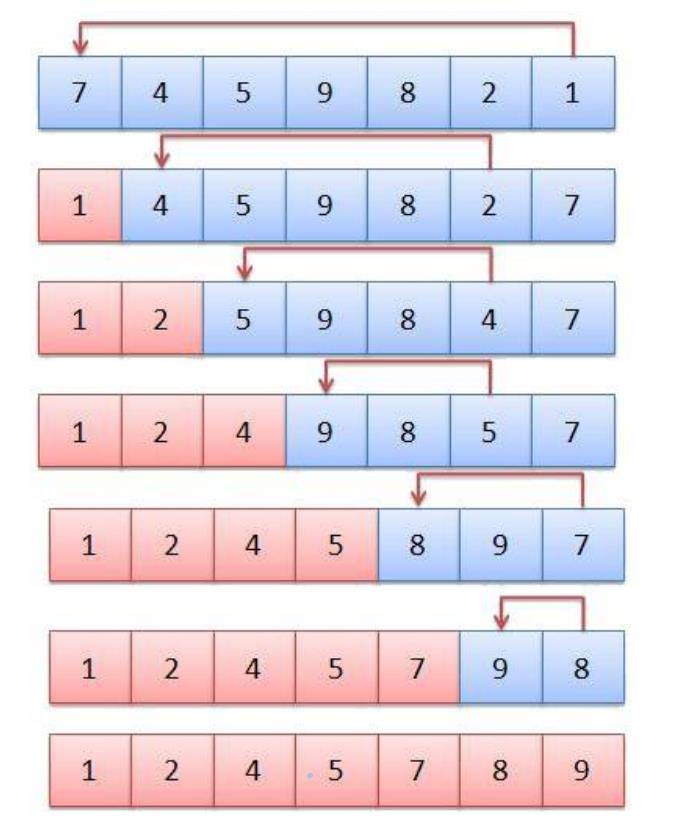
上面那个就是选择排序的本质,但是一次就选一个最大或者最小是不是有点浪费,我们一次同时选到最大最小,就是会比传统的选择排序快一倍
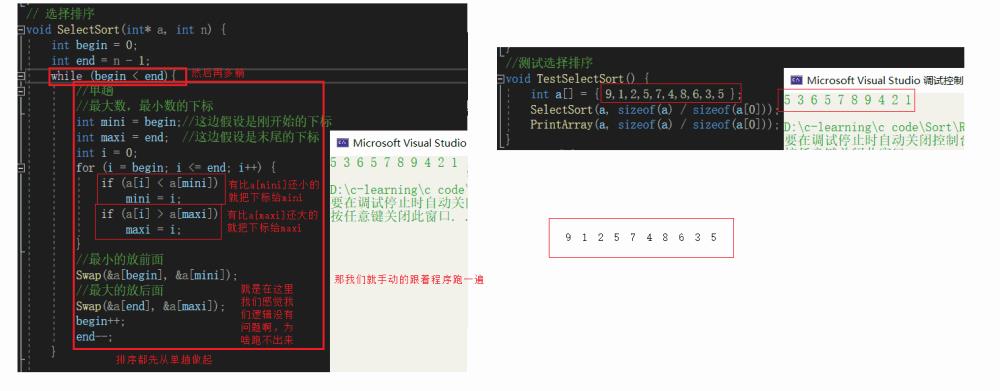
我们基本看到上面代码的缺陷就是我们第一个就是最大是时候,最大的就被换走了,而最小的就被换过来了,但是最大的下标还是标记首位置,把最小的换到后面,也就出现了最小的1在后面的现象
解决方法:既然你最大数的下标和begin重合,那最大数被换走的时候,maxi这个下标也要连带着走

实际上下面 才是我第一次写的代码,直接说下次我再也不写装逼的交换了
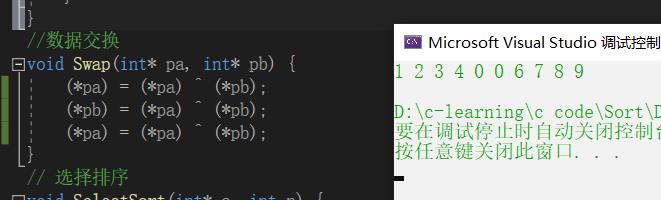
我来道bug恶心之处 看好了跳跳 5 ^ 5 == 0 这就是恶心之处,下次再也不装逼了
数据交换 剥离出来其他函数也会用到 我明明是简洁之人为了一时的高级而忘记了朴素罪过罪过
//数据交换
void Swap(int* pa, int* pb)
int tmp 算法给小码农冒泡排序铭纹,快速排序四极