LeetCode 最热100题 最短路径和，minimum path sum

Posted 2021-12-29 Linux猿

---

🎈 作者：Linux猿

🎈 简介：CSDN博客专家🏆，华为云享专家🏆，Linux、C/C++、面试、刷题、算法尽管咨询我，关注我，有问题私聊！

🎈 关注专栏：LeetCode面试必备100题 （优质好文持续更新中……）🚀

🎈 欢迎小伙伴们点赞👍、收藏⭐、留言💬

---

本题是一道简单的动态规划题目，下面来一起看一下！

一、题目描述

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。 说明：每次只能向下或者向右移动一步。

约束条件：

m == grid.length

n == grid[i].length

1 <= m, n <= 200

0 <= grid[i][j] <= 100

二、测试样例

输入：grid = [[1,3,1],[1,5,1],[4,2,1]]

输出：7

其中，grid 的网格如下所示：

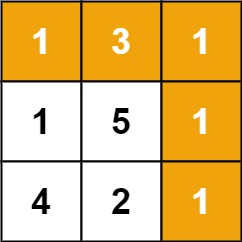
 说明：在上图中，使用颜色标明的路径 1→3→1→1→1 的总和最小。

三、算法思想

本题是一个简单的动态规划题目，可以使用如下的动态方程：

上面公式的含义是：到达方格 (i, j) 的位置的最小和，必定是从 (i-1, j) 或 （i, j-1）而来，当然，(0, 0)点是起点除外。如下图所示：

图 计算dp[i][j]

 其中， 当 i = 0 或 j = 0 的时候需要特殊处理，在上图中是第一列和第一行。

四、代码实现

下面是代码实现，如下所示：

class Solution 
public:
    int minPathSum(vector<vector<int>>& grid) 
        for(int i = 0; i < grid.size(); ++i) 
            for(int j = 0; j < grid[i].size(); ++j) 
                if(i == 0 && i == j)
                    continue;
                int Min = 0x3f3f3f3f;
                if(j-1 >= 0) 
                    Min = min(Min, grid[i][j-1]);
                 
                if(i-1 >= 0) 
                    Min = min(Min, grid[i-1][j]);
                
                grid[i][j] += Min;
            
        
        return grid[grid.size()-1][grid[0].size()-1];
    
;

 五、算法复杂度

5.1 时间复杂度

O(mn)，在上述算法中，使用了两层 for 循环，分别是 m 和 n 次遍历，因为是嵌套的 for 循环，故时间复杂度为 O(mn)。

5.2 空间复杂度

O(1)，在上述算法中，仅仅使用到了个别的变量，故空间复杂度为O(1)。

六、总结

动态规划题目重要的是要推到出动态方程，动态方程一般是从某一点推出是由哪些状态可以组合而成。

关注下方👇👇👇公众号👇👇👇，获取更多优质内容🤞（比心）！