《算法图解》读书笔记 - 狄克斯特拉算法(Dijkstra)

Posted 2021-12-29 Leida_wanglin

《算法图解》读书笔记 - 狄克斯特拉算法(Dijkstra)

应用于有向加权图中前往X的最短路径。

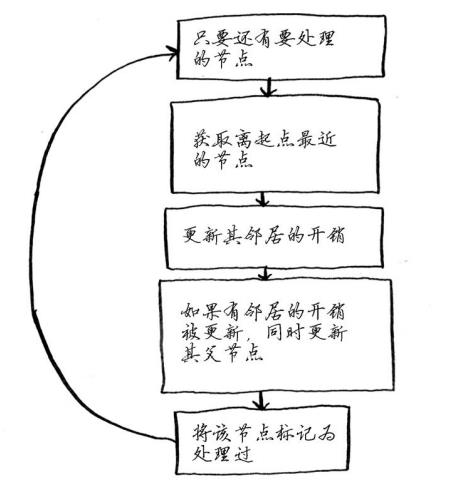
狄克斯特拉算法步骤：
（1）找出“最便宜”的节点，即可在最短时间内到达的节点。
（2）更新该节点的邻居的开销。
（3）重复这个过程，直到对图中的每个节点都这样做了。
（4）计算最终路径。

第一步：找出最便宜的节点。你站在起点，不知道该前往节点A还是前往节点B。前往这两个节点都要多长时间呢？

前往节点A需要6分钟，而前往节点B需要2分钟。至于前往其他节点，你
还不知道需要多长时间。

由于你还不知道前往终点需要多长时间，因此你假设为无穷大（这样做的
原因你马上就会明白）。节点B是最近的——2分钟就能达到。

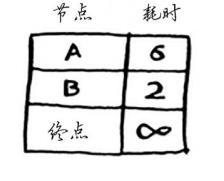
第二步：计算经节点B前往其各个邻居所需的时间。

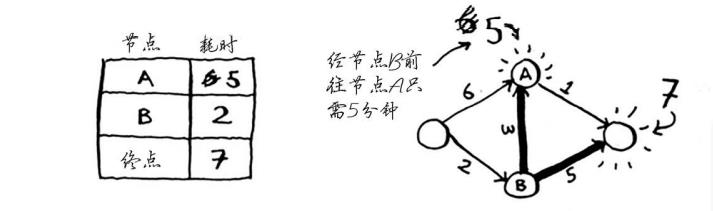
你刚找到了一条前往节点A的更短路径！直接前往节点A需要6分钟。

但经由节点B前往节点A只需5分钟！

对于节点B的邻居，如果找到前往它的更短路径，就更新其开销。在这里，你找到了：
 前往节点A的更短路径（时间从6分钟缩短到5分钟）；
 前往终点的更短路径（时间从无穷大缩短到7分钟）。

第三步：重复！
重复第一步：找出可在最短时间内前往的节点。你对节点B执行了第二步，除节点B外，可在最短时间内前往的节点是节点A。

重复第二步：更新节点A的所有邻居的开销。

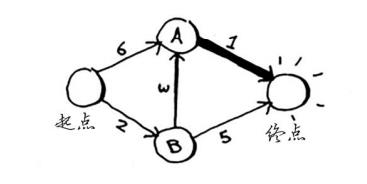
你发现前往终点的时间为6分钟！
你对每个节点都运行了狄克斯特拉算法（无需对终点这样做）。现在，你知道：
 前往节点B需要2分钟；
 前往节点A需要5分钟；
 前往终点需要6分钟。

最后一步——计算最终路径将留到下一节去介绍，这里先直接将最终路径告诉你。

Java代码实现Dijkstra算法

我在这建立三个散列表

1.graph存节点与节点和节点之间的边的值
2.costs存起点与各个节点的权重
3.parents存父节点

小编在这里写的是Java思想，存在一个问题就是HashMap<String, HashMap<String, Integer>>会出现相同Key的Value会被覆盖的问题还没有解决，所以此代码只提供思路。

public class Dijkstra 

    private static HashMap<String, HashMap<String, Integer>> graph = new HashMap<>();

    private static HashMap<String, Integer> costs = new HashMap<>();

    private static HashMap<String, String> parents = new HashMap<>();

    private static List<String> processed = new ArrayList<>();

    public static void dijkstra() 
        //在未处理的节点中找出开销最小的节点
        String node = findLowestCostNode(costs);
        //这个while循环在所有节点都被处理过后结束
        while (node != null) 
            Integer cost = costs.get(node);
            HashMap<String, Integer> neighbors = graph.get(node);
            //遍历当前节点的所有邻居
            for (String n : neighbors.keySet()) 
                Integer new_cost = cost + neighbors.get(n);
                //如果经当前节点前往该邻居更近
                if (costs.get(n) > new_cost) 
                    //就更新该邻居的开销
                    costs.put(n, new_cost);
                    //同时将该邻居的父节点设置为当前节点
                    parents.put(n, node);
                
            
            //将当前节点标记为处理过
            processed.add(node);
            //找出接下来要处理的节点，并循环
            node = findLowestCostNode(costs);
        
    

    //找出开销最低的节点
    public static String findLowestCostNode(HashMap<String, Integer> costs) 
        Integer lowest_cost = Integer.MAX_VALUE;
        String lowest_cost_node = null;
        //遍历所有的节点
        for (String node : costs.keySet()) 
            Integer cost = costs.get(node);
            //如果当前节点的开销更低且未处理过
            if (cost < lowest_cost && parents.containsKey(node) == false) 
                //就将其视为开销最低的节点
                lowest_cost = cost;
                lowest_cost_node = node;
            
        
        return lowest_cost_node;
    

    public static void main(String[] args) 

        graph.put("start", new HashMap<String, Integer>()put("a", 6););
        graph.put("start", new HashMap<String, Integer>()put("b", 2););
        graph.put("a", new HashMap<String, Integer>()put("fin", 1););
        graph.put("b", new HashMap<String, Integer>()put("a", 3););
        graph.put("b", new HashMap<String, Integer>()put("fin", 5););
        graph.put("fin", new HashMap<>());

        costs.put("a", 6);
        costs.put("b", 2);
        costs.put("fin", Integer.MAX_VALUE);

        parents.put("a", "start");
        parents.put("b", "start");
        parents.put("fin", null);

        dijkstra();

        System.out.println(costs.get("fin"));