算法图解-狄克斯特拉算法

Posted 2020-10-31 mofei004

本章内容：

• 加权图-提高或者降低某些边的权重
• 狄克斯特拉算法，能找出加权图中前往x的最短路径
• 图中的环，它导致狄克斯特拉算不管用

7.1狄克斯特拉算法

　　4个步骤：

1. 找出最便宜的节点，即最短时间内前往的节点
2. 对于该节点的邻居，检查是否有前往他们的最短路径，如果有，就更新其开销
3. 重复这个过程，知道对图中的每个节点都这样做了
4. 计算最终路径

7.3负边权

　　狄克斯特拉算法不支持包含负边权的图，因为，狄克斯特拉算法这样假设：对于处理过的海报节点，没有前往该节点的更短的路径。包含负边权的图，可使用贝尔曼-福德算法（bellman-Ford algorithm）。

7.4实现

 1 # the graph
 2 graph = {}
 3 graph["start"] = {}
 4 graph["start"]["a"] = 6
 5 graph["start"]["b"] = 2
 6 
 7 graph["a"] = {}
 8 graph["a"]["fin"] = 1
 9 
10 graph["b"] = {}
11 graph["b"]["a"] = 3
12 graph["b"]["fin"] = 5
13 
14 graph["fin"] = {}
15 
16 # the costs table
17 infinity = float("inf")
18 costs = {}
19 costs["a"] = 6
20 costs["b"] = 2
21 costs["fin"] = infinity
22 
23 # the parents table
24 parents = {}
25 parents["a"] = "start"
26 parents["b"] = "start"
27 parents["fin"] = None
28 
29 processed = []
30 
31 def find_lowest_cost_node(costs):
32     lowest_cost = float("inf")
33     lowest_cost_node = None
34     # Go through each node.
35     for node in costs:
36         cost = costs[node]
37         # If it\'s the lowest cost so far and hasn\'t been processed yet...
38         if cost < lowest_cost and node not in processed:
39             # ... set it as the new lowest-cost node.
40             lowest_cost = cost
41             lowest_cost_node = node
42     return lowest_cost_node
43 
44 # Find the lowest-cost node that you haven\'t processed yet.
45 node = find_lowest_cost_node(costs)
46 # If you\'ve processed all the nodes, this while loop is done.
47 while node is not None:
48     cost = costs[node]
49     # Go through all the neighbors of this node.
50     neighbors = graph[node]
51     for n in neighbors.keys():
52         new_cost = cost + neighbors[n]
53         # If it\'s cheaper to get to this neighbor by going through this node...
54         if costs[n] > new_cost:
55             # ... update the cost for this node.
56             costs[n] = new_cost
57             # This node becomes the new parent for this neighbor.
58             parents[n] = node
59     # Mark the node as processed.
60     processed.append(node)
61     # Find the next node to process, and loop.
62     node = find_lowest_cost_node(costs)
63 
64 print "Cost from the start to each node:"
65 print costs

dijkstras_algorithm.py

字典graph描述了一个图，如下所示：

 

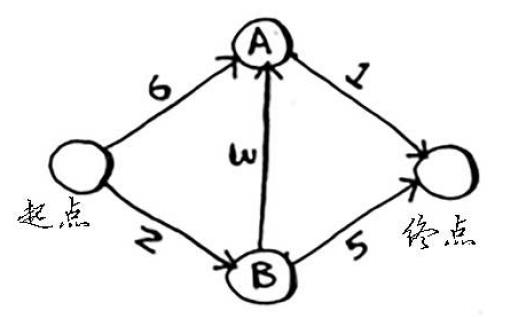
costs描述了每个节点的开销；

parents描述了一个父节点散列表。

算法逻辑简述如下：

• 查找开销最低的节点，获取该节点开销和邻居，即以此节点为起始点的权值和路径，这里是B节点。
• 计算通过B节点到达其邻居的开销，并与从起点到达B邻居的开销对比。如图：到达A节点新开销较小，更新到达A节点的散列表开销值，并把A的父节点改为B；比较B节点到终点的路径2+5<无穷大，故将终点的路径由无穷大改为7，父节点改为B。
• 将B节点标记为处理过。
• 重复步骤1，查找出开销最低的节点即A；此时A的开销是5，终点的开销是7。
• 重复步骤2，A只有一个邻居节点即终点，对比通过A到达终点的开销和已有的数据（7)，更新到达终点的开销为6，并更新终点的父节点为A。
• 所有的节点都查找过后，算法结束。通过父节点散列表可以得到最优路径；通过开销散列表可得到最少到达终点的开销。

7.6小结

• 广度优先搜索用于非加权图中从查找最短路径
• 狄克斯特拉算法用于加权图中查找最短路径
• 仅当权重为正时，狄克斯特拉算法才管用
• 如果图中包含负权边，请使用贝尔曼-福德算法