狄克斯特拉(Dijkstra)算法详解

Posted 2023-04-06 wopelo

1.前言

最近在看《算法图解》，其中第七章狄克斯特拉算法个人感觉并没有讲的清楚，比如看完7.1节给人的感觉是狄克斯特拉算法会遍历图中的每一条边，后续狄克斯特拉不适用负权边的说法就站不住脚了。后续在查阅诸多资料之后，总结文章一篇，尽可能以通俗易懂且思路清晰的方式来讲解狄克斯特拉算法。

2.简介

狄克斯特拉算法用于寻找在加权图中前往目标节点的最短路径，加权图是对边进行加权的图。

2.1.定理

设想这样一个场景——在一个没有负权边的有向图中，如果从起点直接到节点A的开销小于从起点直接到节点B的开销，那么即使从起点出发经过节点B还有其他路径可以到达节点A，其总开销也会大于从起点到节点A的开销。

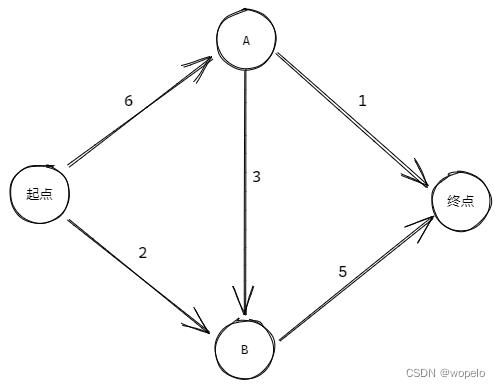
比如在上图中，起点到A的开销为3，这个开销一定小于从起点开始经其他节点到A的总开销，因为从起点到B的开销就已经大于从起点到A的开销。
上面推论的结果就是——最短路径的子路径仍然是最短路径 。比如在上图中，如果最短路径经过了A，那么在最短路径中从起点到A的子路径一定是所有从起点到A的路径中最短的那条。
这个结论可能有点反直觉，因为我们可能会认为虽然前面的子路径不是最短的，但只要后面的子路径选的好，加起来仍然可以得到最短路径。但我们可以这样理解，在当前的最短路径中，点A到终点的路径保持不变，将起点到点A的路径设为L1。如果L1不是起点到点A最短的路径，则存在起点到点A的另外一条路径L2使得L2 < L1，将L1替换成L2，即可得到一条比当前最短路径还要短的路径，那么当前路径就不是最短路径了。路径上的每个点都能以此类推。由此可以证明在没有负权边的情况下，最短路径的子路径仍然是最短路径。
这也解释了为什么狄克斯特拉算法每次都从当前节点开销最少的邻居节点开始下一轮处理。

2.2.术语

• 权重：狄克斯特拉算法用于每条边都有关联数字的图，这些数字称为权重
• 加权图/非加权图：带权重的图称为加权图，不带权重的图称为非加权图
• 广度优先搜索：计算非加权图中的最短路径
• 狄克斯特拉算法：计算加权图中的最短路径
• 环：在图中，如果可以从一个节点出发，走一圈后又回到这个点，则说明图中存在环，绕环的路径不可能是最短路径。在无向图中，每条边就是一个环，狄克特拉斯算法只适用于有向无环图，且没有负权边
• 开销：从一个点到另一个点所经历的边的权重之和，一般加权图的最短路径指的是权重之和最小的那条路径

3.算法步骤

狄克斯特拉算法可分为5步：

1. 找出从起点出发，可以前往的、开销最小的未处理点
2. 对于该节点的邻居，检查是否有前往他们的更短路径，如果有，则更新其开销
3. 将该节点加入已处理队列中，后续不再处理该节点
4. 重复1-4步，直到对图中除了终点的所有节点都进行了检查
5. 得到最终路径

我们通过两个例子来体验上述步骤。

3.1.示例1

找出下图中，从起点到终点的最短路径

准备一张表，存储从起点到各个节点的开销及其父节点，作用是方便最后找出最短路径和最短路径的长度。
初始化时，设起点开销为0，其他节点开销为 inf （无限大），算法结束的条件就是除终点外的所有节点都被处理了。

节点	父节点	开销	是否已处理
起点	-	0	否
A	-	inf	否
B	-	inf	否
终点	-	inf	-

找出当前开销最小的未处理节点，得到起点。起点的邻居是A和B，将其他不能直接到达的节点开销保持为 inf ，更新表：

节点	父节点	开销	是否已处理
起点	-	0	是
A	起点	6	否
B	起点	2	否
终点	-	inf	-

继续找出当前开销最小的未处理节点，得到节点B，计算经节点B前往其各个邻居的开销：

• B到A距离为3，加上起点到B的距离，得从起点经B到达A开销为5，小于之前从起点直接到A的开销
• B可到达终点，加上起点到B的距离，得从起点经B到达终点开销为7

更新表：

节点	父节点	开销	是否已处理
起点	-	0	是
A	B	5	否
B	起点	2	否
终点	B	7	-

至此B节点的所有邻居处理完毕，将B标识为已处理：

节点	父节点	开销	是否已处理
起点	-	0	是
A	B	5	否
B	起点	2	是
终点	B	7	-

重复上面的过程，找出当前开销最小的未处理节点，得到A，计算经节点A前往其各个邻居的开销：

• A到终点距离为1，加上起点到A的最短距离5，得6，小于之前从起点经B到达终点的距离

更新表：

节点	父节点	开销	是否已处理
起点	-	0	是
A	B	5	否
B	起点	2	是
终点	A	6	-

至此A节点的所有邻居处理完毕，将A标识为已处理：

节点	父节点	开销	是否已处理
起点	-	0	是
A	B	5	是
B	起点	2	是
终点	A	6	-

到此所有除了终点的节点都经过检查，得出从起点到终点最短距离为6，最短路径通过终点的父节点逐级向上追溯为：起点 -> B -> A -> 终点。

3.2.示例2

示例2由示例1改变节点B到节点A路径的方向而来，通过该示例可以更好的理解狄克斯特拉算法的处理过程。

同样的操作，准备一张表：

节点	父节点	开销	是否已处理
起点	-	0	否
A	-	inf	否
B	-	inf	否
终点	-	inf	-

找出当前开销最小的未处理节点，得到起点，起点的邻居是A和B，更新表：

节点	父节点	开销	是否已处理
起点	-	0	是
A	起点	6	否
B	起点	2	否
终点	-	inf	-

找出当前开销最小的未处理节点，得到节点B，更新表：

节点	父节点	开销	是否已处理
起点	-	0	是
A	起点	6	否
B	起点	2	是
终点	B	7	-

找出下一个开销最小的未处理节点，得到节点A，对节点A的处理就和示例1有所不同了。
节点A有两个邻居：节点B和终点。但节点B已经处理过了，这意味着当前由起点前往节点B的开销最少的路径已经被发现了，结合之前的定理，这意味着两点：

• 从起点到节点B的开销不可能小于2
• 如果最短路径经过了节点B，那最短路径中有起点到B的路径一定是 起点 -> B 这条路径

综上，不必要检查 A-> B 这条路径的开销，只需要检查 A -> 终点 这条路径的开销。
由于 起点 -> A -> 终点 这条路径的开销没有小于 7，所以不更新A邻居节点的开销，只将A置为已处理即可：

节点	父节点	开销	是否已处理
起点	-	0	是
A	起点	6	是
B	起点	2	是
终点	B	7	-

到此所有除了终点的节点都经过检查，得出从起点到终点最短距离为7，最短路径通过终点的父节点逐级向上追溯为：起点 -> B -> 终点
需要注意的是，这次我们只找到了其中一条最短路径，因为 起点 -> A -> 终点 这条路径的开销也是 7。

4.实现

下面用python展示从下图中找出用乐谱交换钢琴需要额外支付费用最少的路径

# 使用狄克斯特拉在加权有向图中寻找最短路径
from cmath import inf

# 构建图
map = 
map['乐谱'] = 
map['乐谱']['唱片'] = 5
map['乐谱']['海报'] = 0
map['唱片'] = 
map['唱片']['吉他'] = 15
map['唱片']['架子鼓'] = 20
map['海报'] = 
map['海报']['吉他'] = 30
map['海报']['架子鼓'] = 35
map['吉他'] = 
map['吉他']['钢琴'] = 20
map['架子鼓'] = 
map['架子鼓']['钢琴'] = 10

# 初始化table中的行
def initRow(costs, key, cost):
  costs[key] = 
  costs[key]['father'] = None
  costs[key]['cost'] = cost
  costs[key]['isChecked'] = False

# 获取当前开销最少的节点
def findLowerCostNode(costs):
  key = None
  cost = float(inf)

  for name in costs:
    item = costs[name]
    if (item['isChecked'] == False and item['cost'] < cost ):
      cost = item['cost']
      key = name

  return key

def dijkstra(map, start, end):
  # 初始化表
  costs = 
  initRow(costs, start, 0)

  key = findLowerCostNode(costs)

  while (key != None and key != end): 
    # 获取邻居
    neighbors = map[key].keys()

    # 检查到邻居的开销
    for neighbor in neighbors:
      # 如果邻居不在costs中，则添加
      if (neighbor not in costs):
        initRow(costs, neighbor, float(inf))

      # 获取到key的开销
      newCost = map[key][neighbor] + costs[key]['cost']
      # 如果经key到邻居的开销小于已有开销
      if (newCost < costs[neighbor]['cost']):
        costs[neighbor]['cost'] = newCost
        costs[neighbor]['father'] = key
    
    # key的所有邻居都检查过了
    costs[key]['isChecked'] = True
    key = findLowerCostNode(costs)

  # 打印结果
  key = end
  routes = []

  while (key != None):
    node = costs[key]
    routes.insert(0, key)
    father = node['father']
    key = father
    
  print(f'最短路径为: "->".join(routes)，开销costs[end]["cost"]')
  # print(costs)

dijkstra(map, '乐谱', '钢琴')

5.负权边

负权边即权重为负的边，如果有负权边，则不能使用狄克斯特拉算法，而应该使用贝尔曼-福德算法。

还是用这张图举例，如果X、Y、Z中有负数，那经过B到的A的开销可能就比3小了，即使从起点到B的开销大于从起点到A开销。

6.参考

图最短路径算法之迪杰斯特拉算法（Dijkstra）

dijkstra算法模板（优先队列优化）

dijkstra算法是由荷兰计算机科学家狄克斯特拉于1959 年提出的，因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法，解决的是有

向图中最短路径问题。迪杰斯特拉算法主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。 

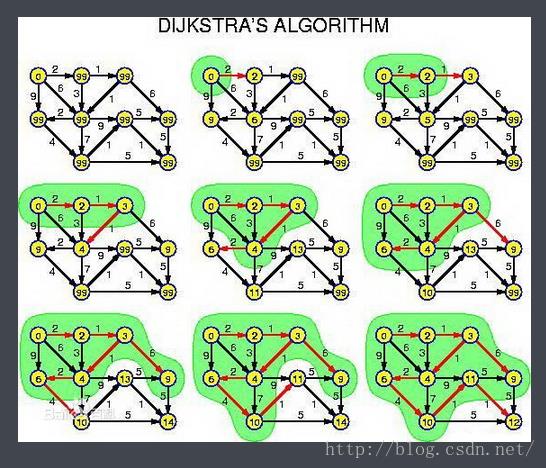
常规的dijkstra算法复杂度较高，为O(n^2)，因为要花大量时间来找当前已知的距顶点距离最小的值，所以用优先队列（值小的先出队列）来优化，可省大量时间。

 

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<stack>
#include<queue>
#include<vector>
using namespace std;


#define INF  0x3f3f3f3f   //定义一个很大的数


struct Node

int num,val;   //存放结点编号和到初始点的距离 
nod;


priority_queue<Node> qq;;   //优先从小到大


bool operator < (Node a,Node b)

if(a.val == b.val) return a.num>b.num;
return a.val>b.val;              //先出小 



int book[100];  //检查这个点是否用过 
int dis[100];     //到原点最短距离 
int D[100][100];  //记录路径长度
int V,E; 


int main()

int a,b,d;
while(cin>>V>>E && V&& E)  //输入顶点数和边数 

while(!qq.empty()) qq.pop(); //清空
memset(book,0,sizeof(book));
memset(D,-1,sizeof(D)); 

for(int i=0;i<E;i++)

cin>>a>>b>>d;
D[a][b] = D[b][a] = d;


for(int i=2;i<=V;i++)
dis[i]=INF;

dis[1]=0;
nod.num=1;
nod.val=0;

qq.push(nod);   //将起点放入队列 

while(!qq.empty())  //不为空时 


for(int i=2;i<=V;i++)

if(D[qq.top().num][i] != -1  &&dis[i]>dis[qq.top().num] + D[qq.top().num][i]) 


dis[i]=dis[qq.top().num] + D[qq.top().num][i];
nod.num=i; nod.val=dis[i];
qq.push(nod);



qq.pop();


for(int i=1;i<=V;i++)

cout<<"初始点到"<<i<<"点的距离为："<<dis[i]<<endl;
 


return 0;