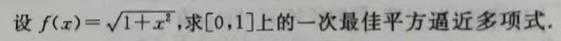《数值分析》-- The great 平方逼近
Posted 胜天半月子
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了《数值分析》-- The great 平方逼近相关的知识,希望对你有一定的参考价值。
The great 平方逼近:最佳平方逼近
一、最佳平方逼近及计算

- 定义

span中会给出 φ i ( x ) \\varphi_i(x) φi(x)对应的具体函数,稍后看习题就会明白。 - 讨论
S
∗
(
x
)
S^*(x)
S∗(x)的计算
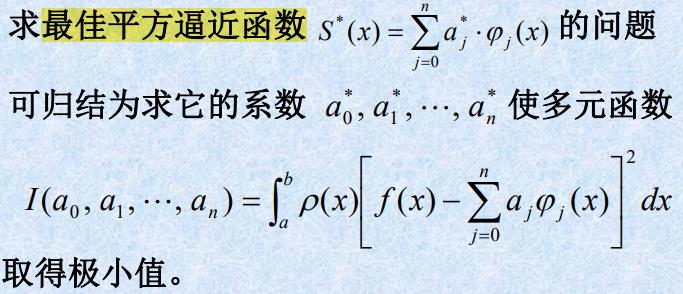
由于 I ( a 0 , a 1 , . . , a n ) I(a_0,a_1,..,a_n) I(a0,a1,..,an)是关于 a 0 , a 1 , . . , a n a_0,a_1,..,a_n a0,a1,..,an的二次函数,故利用多元函数取得极值的必要条件,可得
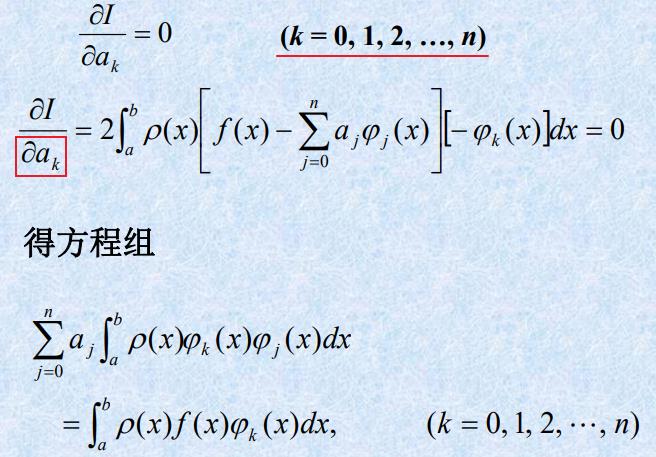




n阶矩阵(方正)的行向量或列向量线性无关,则秩等于n,所以矩阵的行列式不等于0,矩阵可逆。
- 误差的计算⭐
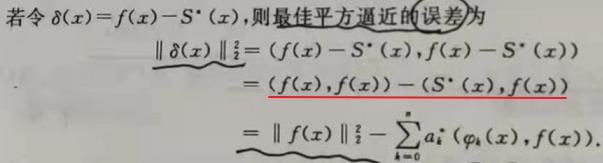

二、用正交多项式作最佳平方逼近
-
定义

习题 -
补充

通常采用该方法求最佳平方逼近多项式。
习题
-
例题

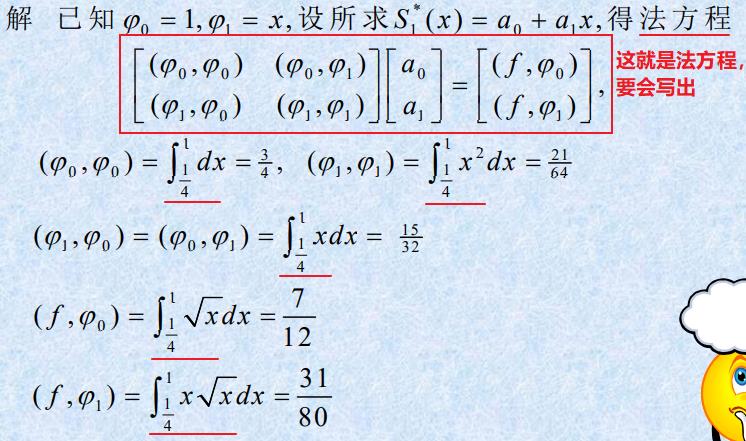
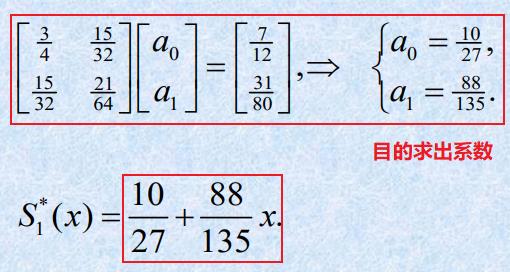




注意: φ i ( x ) \\varphi_i(x) φi(x)题目没有给出,因此我们需要明白 φ i ( x ) \\varphi_i(x) φi(x)中我们需要值。以及写出法方程!

- 平方逼近的误差

- 误差
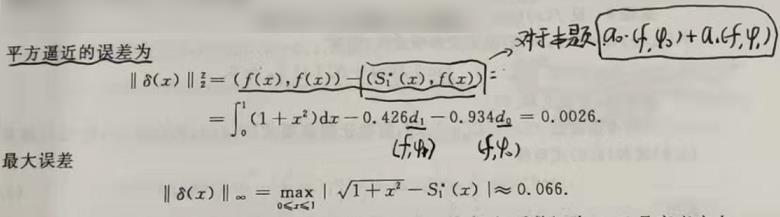
-
例题
- 利用勒让德多项式序列求 f ( x ) = e x f(x)=e^x f(x)=ex在[-1,1]上的三次最佳平方逼近多项式。
-
S ∗ ( x ) 与 a k S^*(x)与a_k S∗(x)与ak
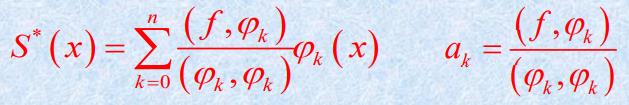
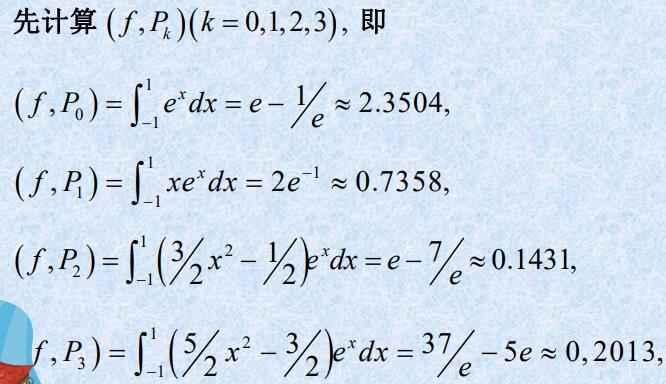

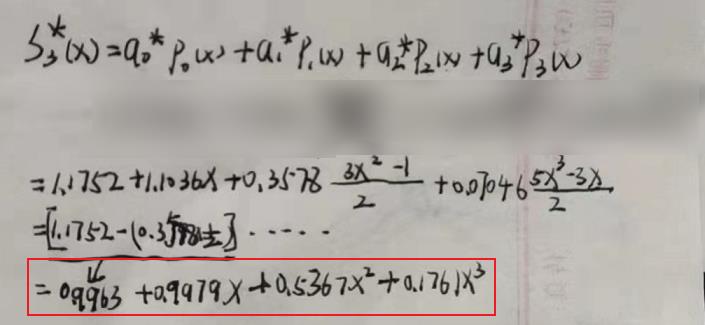
-
a k a_k ak的计算
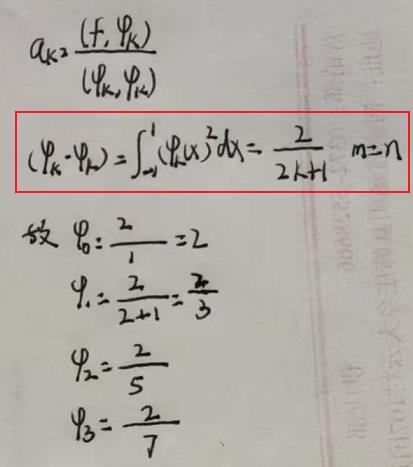
-
均方误差
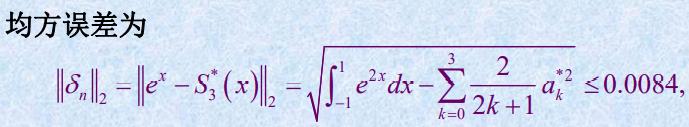
以上是关于《数值分析》-- The great 平方逼近的主要内容,如果未能解决你的问题,请参考以下文章
99插值法,函数逼近,曲线拟和,数值积分,数值微分,解线性方程组的直接方法,解线性方程组的迭代法,非线性方程求根,常微分方程的数值解法