《数值分析》-- 函数逼近线性空间范数权函数

Posted 2021-12-28 胜天半月子

文章目录

• 问题
• 一、线性空间及相关概念
• • 1.1 线性相关 ⭐
  • 1.2 范数与赋范线性空间
• 二、常用的度量标准 ⭐
• 三、内积空间
• 习题

---

问题

代数插值有缺陷:如龙格现象


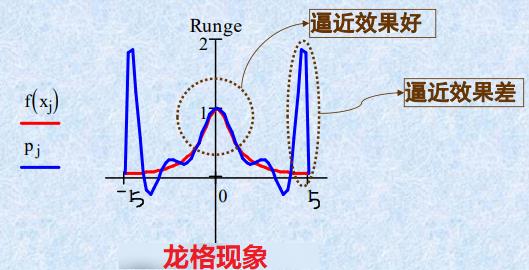
如何在给定精度下，求出计算量最小的近似式，这就是函数逼近要解决的问题。

• 函数逼近问题
  

---

一、线性空间及相关概念

1.1 线性相关 ⭐

设S是数域P上的线性空间,元素$x_1,...,x_n\in S$,若存在不全为0的数$a_1,a_2,...,a_n\in P$,使得

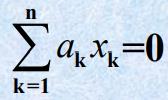
称元素$x_1,...,x_n$线性相关;否则称为线性无关(即系数全为0).
若$x_1,...,x_n$线性无关,称 span$x_1,...,x_n$ 为由基$x_1,...,x_n$生成的$n$维线性空间 .记为$S$.

• 函数系的线性相关
  

1.2 范数与赋范线性空间

对线性空间$S$ 中元素的 大小进行衡量,需要引入范数概念。

• 范数⭐
  
  
  
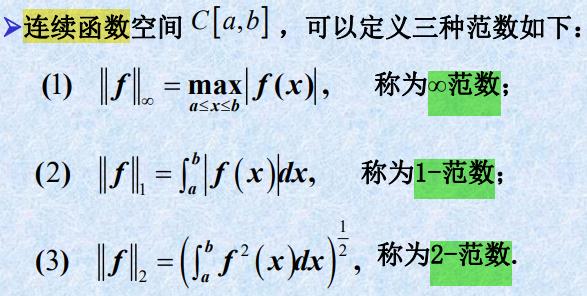
  习题

---

二、常用的度量标准 ⭐

1. 最佳一致逼近
   
   对应∞范数
2. 最佳平方逼近
   
   对应2-范数

---

三、内积空间

1. 定义
   

2. 内积的性质
   

3. 权函数的定义
   

4. 欧氏空间与连续函数空间
   

5. Gram矩阵

• 定义
  
• 定理
  

---

习题

• 例题

1.