现代信号处理17 - 基于滤波器组的谱估计

Posted 2021-12-28 Ciaran-byte

基于滤波器组的谱估计–Filter-Bank Method

文章目录

• 基于滤波器组的谱估计--Filter-Bank Method
• • 1. 滤波器组
  • • 1.1 分段处理谱估计问题
    • 1.2 滤波器作为谱估计的手段
    • 1.3 滤波器与滤波器组
  • 2. 滤波器组与周期图之间的关系
  • 3. 数据无关的滤波器组方法--Slepian 滤波器
  • • 3.1 设计目标
    • 3.2 计算
    • • 3.2.1 约束条件的计算
      • 3.2.2 优化目标的计算
      • 3.2.3 对γ矩阵的分析
      • 3.2.4 slepian window
  • 4. Multitaper
  • • 4.1 周期图谱中的trade off
    • 4.2 slepian window与周期图谱估计
    • • 4.2.1 Multitaper
      • 4.2.2 证明不同滤波器谱分析结果不相关
      • 4.2.3 小结
  • 5. 数据相关的谱估计方法-Capon Spectrum
  • • 5.1 问题引入
    • 5.2 约束条件与目标函数
    • 5.3 与slepian的对比
    • 5.4 计算
    • 5.5 小结

1. 滤波器组

  首先我们介绍一下，什么是滤波器组

1.1 分段处理谱估计问题

  通常随机信号是无限长的，连续的。但是实际信号的经过采样之后的，就变成了离散的，有限长度的。

  现在我们想用有限长的数据估计随机信号的功率谱

$$Z(t)\Rightarrow Z(k){}_{k=1}^{N-1}$$

  我们实际是希望得到每一个频点上的功率谱的分量。但是我们只有有限长的数据，这是不可能实现的事情。

  我们只能降低要求。就是不求全部频率点的功率谱，而是划分一个小区间，就用有限的数据，求这一个小区间的功率谱的和

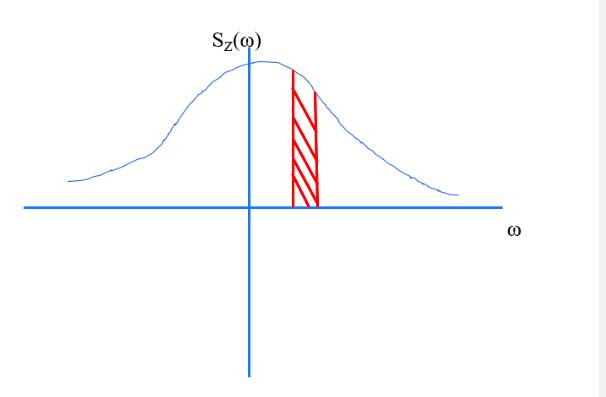
  现在问题就变成了。我们的数据经过采样之后，就划分出了一段工作频带，频带取决于采样率。采样频率的倒数，就是带宽。然后将频宽归一化到(-pi,pi)

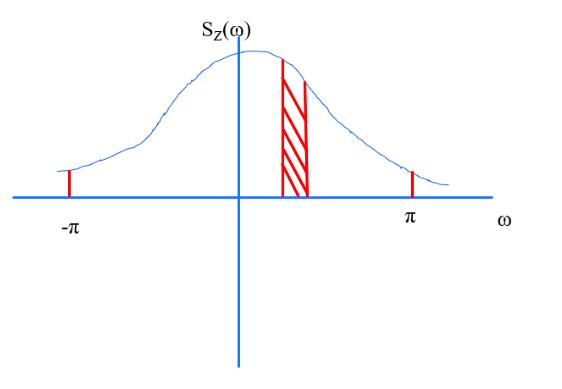
  在这个频带内可以划分出很多的小段。只要划分出的小段的数量，比采样的数据数目少即可。

1.2 滤波器作为谱估计的手段

  为了能够获得这个小段，我们只需要让信号通过一个滤波器即可，滤波器的通带就是这个小段

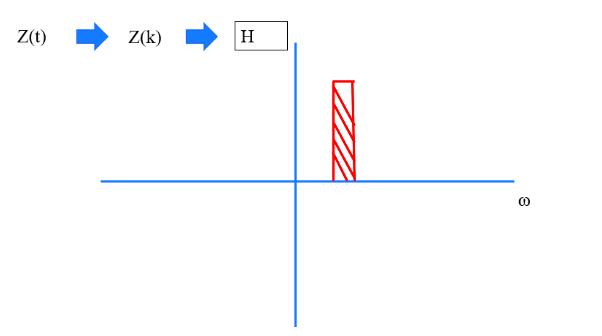
  只要我们滤波器是理想的，我们就能够得到这一小段内功率的和

  因此滤波器就变成了解决谱分析问题的工具

1.3 滤波器与滤波器组

  为什么会有滤波器组的概念呢，因为我们一个滤波器只能得到一个频点周围的功率的和。

  如果我们想看很多频点周围的功率的和，我们就要让滤波器滑动起来，就有了滤波器组的概念

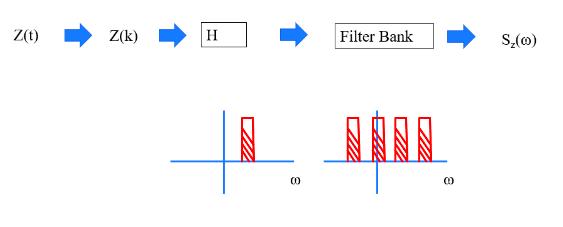
  我们得到了多个频点的功率和之后，就能够得到一个相对比较准确的谱估计了

2. 滤波器组与周期图之间的关系

  我们用滤波器组的观点来重新看待周期图

$${\hat{S}}_Z(\omega )=\frac{1}{N}|\sum _{k=1}^{N-1}Z(k)exp(-j\omega k){|}^2$$

  改变一下形式，在模里面加一个相位,因为相位改变对模没有影响，所以变换前后值不变

$${\hat{S}}_Z(\omega )=\frac{1}{N}|\sum _{k=1}^{N-1}Z(k)exp(j\omega (N-k)){|}^2$$
  这样做是为了构造卷积的样子

$$\begin{gathered} \text{Let }{h}_k=e(j\omega k) \\ k=0,1,...,N-1 \end{gathered}$$

$$\text{Then }{\hat{S}}_Z(\omega )=\frac{1}{N}|\sum _{k=0}^{N-1}Z(k)h_{N-k}(\omega ){|}^2$$

  再变形下，让式子更加接近卷积

$$\begin{gathered} =\frac{1}{N}|\sum _{k=0}^{\infty }Z(k)h_{N-k}(\omega ){|}^2 \\ {h}_k(\omega )=\begin{array}{ll}exp(j\omega k)& \text{k=1,...,N-1 }\\ 0& \text{others }\end{array} \end{gathered}$$

  然后我们计算下滤波器的频率响应

$$\begin{gathered} H({\omega }^{\prime })=\sum _{k=1}^{N-1}{h}_k({\omega }^{\prime })exp(-j{\omega }^{\prime }k) \\ =\sum _{k=1}^{N-1}exp(j(\omega -{\omega }^{\prime })k) \end{gathered}$$

$$|H({\omega }^{\prime })|=\frac{sin(\frac{N}{2}(\omega -{\omega }^{\prime }))}{sin(\frac{1}{2}(\omega -{\omega }^{\prime }))}$$

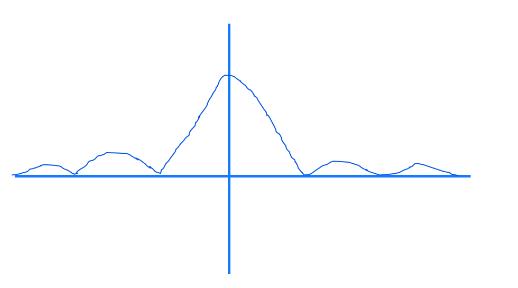
  上图是ω为0的时候的频率响应。如果要滑动的话，就是让这个图沿着ω轴滑动即可。我们从滤波器角度审视周期图的话，发现因为主瓣模糊和旁瓣泄漏，这个滤波器其实并不是非常好。

  我们可以发现，周期图就是在用一个滤波器在频率轴进行滑动，但是滤波器的质量却离理想的差很远。

  但是周期图的滤波器效果不好，只是因为我们没有对这个滤波器进行单独的设计。我们只是根据功率谱的定义式，然后通过离散化的方式得到了周期图。

  下面我们就要对通过对滤波器进行单独设计，然后得到更好的谱估计。

3. 数据无关的滤波器组方法–Slepian 滤波器

3.1 设计目标

  也就是我们要找到一组h_k，我们对他的频响有要求。我们先在零频上找这个滤波器，然后可以通过修改相位的方法进行滑动，找到滤波器组。

  首先，我们要求在整个工作频带内的通过能力是归一化的

h k k = 0 N − 1 → H ( ω ) 1 2 π ∫ − π π ∣ H ( ω ) ∣ 2 d ω = 1 \\ h_k \\_k=0^N-1 \\rightarrow H(\\omega) \\\\ \\frac12\\pi \\int_-\\pi^\\pi |H(\\omega)|^2 d\\omega = 1 hk​k=0N−1​→H(ω)2π1​∫−ππ​∣H(ω)∣以上是关于现代信号处理17 - 基于滤波器组的谱估计的主要内容，如果未能解决你的问题，请参考以下文章

现代信号处理 04 - 正交化与维纳滤波

滤波器设计

现代信号处理 06 - 卡尔曼滤波

现代信号处理与应用

现代信号处理09 - 自适应与LMS

基于维纳滤波的图像运动模糊还原matlab仿真