对极线的求解
Posted 涂涂啊
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了对极线的求解相关的知识,希望对你有一定的参考价值。
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
前言
本实验的任务是利用所学知识实现两幅图之间F矩阵的求解,最后利用求解的F显示出20组对应点对应的对极线。
实验用图:


一、基本原理
两幅视图存在两个关系:第一种,通过对极几何一幅图像上的点可以确定另外一幅图像上的一条直线;另外一种,通过上一种映射,一幅图像上的点可以确定另外一幅图像上的一个点,这个点是第一幅图像通过光心和图像点的射线与一个平面的交点在第二幅图像上的影像。第一种情况可以用基础矩阵来表示,第二种情况则用单应矩阵来表示。而本质矩阵则是基本矩阵的一种特殊情况,是在归一化图像坐标下的基本矩阵。 基本矩阵体现了两视图几何(对极几何,epipolar geometry)的内在射影几何(projective geometry)关系,基本矩阵只依赖于摄像机的内部参数K和外部参数R、t。
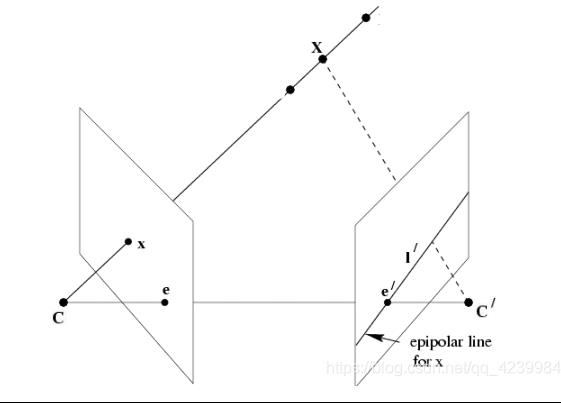
上图是一个两视图的几何描述,其中C、C’是两个相机的光心,两点连线CC’称为基线,基线与图像平面的交点e、e′称为对极点,其中l′是图像点x对应的对极线。通过图2我们可以知道,左侧相机的图像平面上的每一点x,在另外一幅图像上必在一条对极线l′与之对应,且第二幅图像上与点x对应的点x′必定在l’上。反之亦成立。
通过图2我们可以看到存在一个从一副图像上的点到另外一幅图像与之对应的对极线的映射x→l′。而基础矩阵就表示了这种从点到直线的射影映射关系、图像中任意对应点 x-x’之间的约束关系。这种关系用公式可以表达为:

其中,x是像素平面一上一点的齐次坐标,x’像素平面二上与x对应的一点,F被称为像素平面一到像素平面二的基础矩阵,是一个3*3的齐次矩阵,秩为2。通过式(2-1),我们可以推导出,F的转置矩阵为像素平面二到像素平面一的基础矩阵。将式(2-1)用齐次坐标展开有:
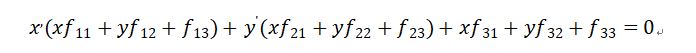
F中有9个元素,将f33归一化之后,剩下8个未知数,需要八个方程才能求出唯一解。因此求解F至少需要8组对应点。但是取点时要注意,这8组对应点必不能存在共线的三组点。
其它原理可以参考我的另一篇文章:
https://blog.csdn.net/qq_43671173/article/details/121605942
二、实现步骤及实验结果
1.实现步骤
1)用SIFT算法提取出两幅图特征点以及特征描述子,并用匹配器进行匹配,得到对应点集合;
2)Ransac筛选匹配点:在对应点集合中随机选八组点求解出一个基础矩阵,记为F’,计算第二幅图中对极点与F’矩阵映射出来对极线的距离,若距离小于阈值即为内点,如此迭代一定次数,取内点最多一次的内点作为最后的筛选结果;
3)将筛选到的点,列方程组(如式(3-1)),利用SVD分解求极小范数最小二乘解,即为F;
4)由于Ransac筛选过的点仍然存在误差,所以求得的F矩阵秩很可能大于2。为了让F的秩为二,我们把F 作SVD分解,将对角矩阵最后一个元素置零,再和分解后的U、V重新组合,得到一个新的秩为2的矩阵;
5)取二十组对应点,分别求他们的对极线并显示出来。
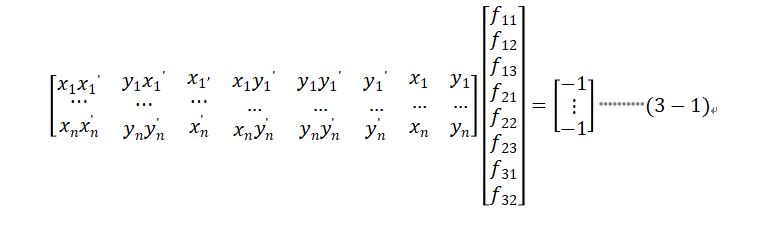
2.实验结果
SIFT匹配后的结果:

RANSAC筛选后的结果:

20组对应点和它们对应的对极线(蓝线为秩为3时的对极线,白线为秩为2时的对极线,绿色的点为我们取的点):


3.实验分析
F秩为3和秩为2时得到的对极线位置变化不大,可能时筛选到的点都比较可靠,求得的F误差也不大造成的。为了验证我们求得对极线的正确性,我将对应点都显示在各自的图像上了,若点基本都在对极线上则求取的F是正确的。通过观察,我们显示的点都基本靠近对极线,所以我们求的F是基本是对的。
提示:这里对文章进行总结:
例如:以上就是今天要讲的内容,本文仅仅简单介绍了pandas的使用,而pandas提供了大量能使我们快速便捷地处理数据的函数和方法。
实现代码(opencv-C++)
#include <iostream>
#include <stdio.h>
#include "opencv2/core.hpp"
#include "opencv2/core/utility.hpp"
#include "opencv2/core/ocl.hpp"
#include "opencv2/imgcodecs.hpp"
#include "opencv2/highgui.hpp"
#include "opencv2/features2d.hpp"
#include "opencv2/calib3d.hpp"
#include "opencv2/imgproc.hpp"
#include"opencv2/flann.hpp"
#include"opencv2/features2d.hpp"
#include"opencv2/ml.hpp"
#include <opencv2/imgproc/types_c.h>
#include "opencv2/core/operations.hpp"
#include "opencv2/core/core.hpp"
#include<cmath>
#include <opencv.hpp>
#include "opencv2/features2d.hpp"
#include "opencv2/core/types_c.h"
using namespace cv;
using namespace std;
void goodMatches(vector<DMatch>& matches, Mat& imageDesc1, vector< DMatch >& good_matches, int n);
void FITSVD(vector<KeyPoint>& keyPoints1, vector<KeyPoint>& keyPoints2, vector<DMatch>& matches, Mat& F);
void fitLineRansac(vector<KeyPoint>& keyPoints1, vector<KeyPoint>& keyPoints2, vector<DMatch>& matches, vector<DMatch>& inlierMatch, int iterations, double sigma);
int main(int argc, char* argv)
//读取图像
Mat image01 = imread("E:/project/sift-f 2021.05.24/01.jpg",1);
Mat image02 = imread("E:/project/sift-f 2021.05.24/02.jpg",1);
if (image01.empty() || image02.empty())
cout << "Can't read image" << endl;
return -1;
Mat img1, img2, img1_gray, img2_gray;
resize(image01, img1, Size(image01.rows * 0.5, image01.cols * 0.5));
resize(image02, img2, Size(image02.rows * 0.5, image02.cols * 0.5));
cvtColor(img1, img1_gray, CV_BGR2GRAY);
cvtColor(img2, img2_gray, CV_BGR2GRAY);
//提取特征点
vector<KeyPoint>keyPoints1;
vector<KeyPoint>keyPoints2;
int numFeatures = 2000;
Ptr <cv::SIFT> sift = sift->create(numFeatures);;
sift->detect(img1_gray, keyPoints1);
sift->detect(img2_gray, keyPoints2);
//提取特征描述子
Mat imageDesc1, imageDesc2;
cv::Ptr<SiftDescriptorExtractor>extractor = SiftDescriptorExtractor::create(1800);
extractor->compute(img1_gray, keyPoints1, imageDesc1);
extractor->compute(img2_gray, keyPoints2, imageDesc2);
BFMatcher matcher;
vector<DMatch> matches12;
matcher.match(imageDesc1, imageDesc2,matches12);
Mat image_match2;
drawMatches(img1, keyPoints1, img2, keyPoints2, matches12, image_match2);
imshow("没有经过Rancsanc处理后图片", image_match2);
vector<DMatch> good_matches12;
goodMatches(matches12, imageDesc1, good_matches12, 5);
Mat image_match12;
drawMatches(img1, keyPoints1, img2, keyPoints2, good_matches12, image_match12);
imshow("match12后图片", image_match12);
imwrite("E:/临时文件夹/01.jpg",image_match12);
vector<DMatch> inlinerMatch12;
fitLineRansac(keyPoints1, keyPoints2, good_matches12, inlinerMatch12, 10000, 0.5);
Mat image_linermatch12;
drawMatches(img1, keyPoints1, img2, keyPoints2, inlinerMatch12, image_linermatch12);
imshow("linermatch12", image_linermatch12);
imwrite("E:/临时文件夹/02.jpg", image_linermatch12);
Mat F;
Mat S;
Mat U;
Mat VT;
Mat W = Mat::zeros(3, 3, CV_64FC1);
FITSVD(keyPoints1, keyPoints2, inlinerMatch12, F);
SVD thissvd;
thissvd.compute(F, S, U, VT, SVD::FULL_UV);
cout << S << endl;
for (int c = 0; c < 20; c++)
Mat X1 = (Mat_<double>(3, 1) << keyPoints1[inlinerMatch12[c].queryIdx].pt.x, keyPoints1[inlinerMatch12[c].queryIdx].pt.y, 1);
Mat X2 = (Mat_<double>(3, 1) << keyPoints2[inlinerMatch12[c].trainIdx].pt.x, keyPoints2[inlinerMatch12[c].trainIdx].pt.y, 1);
Mat L1 = F * X2;
Mat L2 = F.t() * X1;
line(img1, Point(0, -L1.at<double>(2, 0) / L1.at<double>(1, 0)), Point(1000, -(L1.at<double>(0, 0) * 1000 + L1.at<double>(2, 0)) / L1.at<double>(1, 0)), Scalar(255, 0, 0), 1, 8, 0);
line(img2, Point(0, -L2.at<double>(2, 0) / L2.at<double>(1, 0)), Point(1000, -(L2.at<double>(0, 0) * 1000 + L2.at<double>(2, 0)) / L2.at<double>(1, 0)), Scalar(255, 0, 0), 1, 8, 0);
circle(img1, Point(keyPoints1[inlinerMatch12[c].queryIdx].pt.x, keyPoints1[inlinerMatch12[c].queryIdx].pt.y), 3, Scalar(0, 255, 0), 2, 8);
circle(img2, Point(keyPoints2[inlinerMatch12[c].trainIdx].pt.x, keyPoints2[inlinerMatch12[c].trainIdx].pt.y), 3, Scalar(0, 255, 0), 2, 8);
imshow("极线2", img2);
imshow("极线1", img1);
imwrite("E:/临时文件夹/05.jpg", img1);
imwrite("E:/临时文件夹/06.jpg", img2);
S.at<double>(2, 0) = 0;
for (int i = 0; i < 3; i++)
W.at<double>(i, i) = S.at<double>(i, 0);
F = U *W * VT;
cout << F << endl;
for (int c=0; c < 20 ; c++)
Mat X1 = (Mat_<double>(3, 1) << keyPoints1[inlinerMatch12[c].queryIdx].pt.x, keyPoints1[inlinerMatch12[c].queryIdx].pt.y, 1);
Mat X2 = (Mat_<double>(3, 1) << keyPoints2[inlinerMatch12[c].trainIdx].pt.x, keyPoints2[inlinerMatch12[c].trainIdx].pt.y, 1);
Mat L1 = F * X2;
Mat L2 = F.t() * X1;
line(img1, Point(0, -L1.at<double>(2, 0) / L1.at<double>(1, 0)), Point(1000, -(L1.at<double>(0, 0) * 1000 + L1.at<double>(2, 0)) / L1.at<double>(1, 0)), Scalar(255, 255, 255), 1, 8, 0);
line(img2, Point(0, -L2.at<double>(2, 0) / L2.at<double>(1, 0)), Point(1000, -(L2.at<double>(0, 0) * 1000 + L2.at<double>(2, 0)) / L2.at<double>(1, 0)), Scalar(255, 255, 255), 1, 8, 0);
circle(img1, Point(keyPoints1[inlinerMatch12[c].queryIdx].pt.x, keyPoints1[inlinerMatch12[c].queryIdx].pt.y), 3,Scalar(0,255,0),2,8);
circle(img2, Point(keyPoints2[inlinerMatch12[c].trainIdx].pt.x, keyPoints2[inlinerMatch12[c].trainIdx].pt.y), 3, Scalar(0, 255, 0),2, 8);
imshow("极线2",img2);
imshow("极线1", img1);
imwrite("E:/临时文件夹/03.jpg", img1);
imwrite("E:/临时文件夹/04.jpg", img2);
waitKey(0);
void goodMatches(vector<DMatch>& matches, Mat& imageDesc1, vector< DMatch >& good_matches, int n)
double max_dist = 0; double min_dist = 100;//最小距离和最大距离
for (int i = 0; i < imageDesc1.rows; i++)
double dist = matches[i].distance;
if (dist < min_dist) min_dist = dist;
if (dist > max_dist) max_dist = dist;
//【7】存下匹配距离小于n*min_dist的点对
for (int i = 0; i < matches.size(); i++)
if (matches[i].distance < n* min_dist)
good_matches.push_back(matches[i]);
void fitLineRansac(vector<KeyPoint>& keyPoints1, vector<KeyPoint>& keyPoints2, vector<DMatch>& matches, vector<DMatch>& inlierMatch, int iterations, double sigma)
vector< DMatch > inlierMatch12;
vector< DMatch > matches_rand;
unsigned int n = matches.size();
if (n <以上是关于对极线的求解的主要内容,如果未能解决你的问题,请参考以下文章