多视几何：对极几何的代数表示--基本矩阵F

Posted 2022-12-04 tina_ttl

对极几何的基本概念中是对对极几何的基本形式进行了描述，但并没有从数学角度对其进行描述，而基本矩阵正是对对极几何的代数描述

1.总述

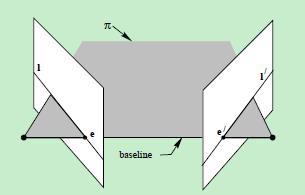
对极几何描述的就是点x和它的对极线l’之间的关系：$l\'=Fx$，其中，矩阵F称为基本矩阵

下面，分别从几何角度和代数角度对上式进行推导

2.几何推导

从几何角度推导关于对极几何方程，如下图所示

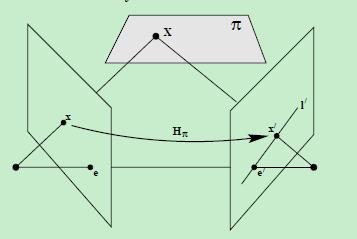
• 图像点x是空间点X在图像1中的投影点，那么，有
  $$x=H_1X\\Rightarrow (1)$$
• 同理，图像点x’是空间点X在图像1中的投影点，那么，有
  $$x\'=H_2X\\Rightarrow (2)$$
• 根据式（1）可以得到
  $$X = H_1^-1x\\Rightarrow (3)$$

• 将式（3）代入式（2）得到
  

  $$x\'=H_2 H_1^-1x \\overset令H_2 H_1^-1=H_\\pi\\rightarrow H_\\pi x \\Rightarrow (4)$$

• 图像点x对应的基线l’是通过点x’和点e’的直线，那么，有
  

  $$l\'=e\'\\times x\'\\Rightarrow (5)$$
  其中的$\\times$为叉乘；

• 将式（4）代入式（5）可以得到
  

  $$l\'=e\'\\times H_\\pi x\\overset令e\'\\times H_\\pi=F\\rightarrow Fx$$

结论（来自多视几何教材）：基本矩阵F可以记为$F=[e\']_\\times H_\\pi$，其中，$H_\\pi$是从一幅图像到另一幅图像通过任意平面$\\pi$的转移映射，而且，因为$[e\']_\\times$的秩为2，$H_\\pi$的秩为3，所以，$F$的秩为3

3.代数推导

仍旧以下图为例，假设两幅图像对应的摄像机矩阵分别为P和P’，光心分别为C和C’

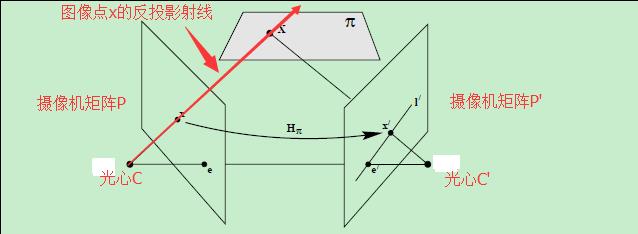
图像点x反投影射线的参数形式为$X(\\lambda) = P^+ x + \\lambda C$

• $\\lambda = 0时$，代表该射线上一个特殊的点$P^+ x$
• $\\lambda = + \\infty 时$，代表该射线上一个特殊的点C

在摄像机2的作用下，这两个特殊的点分别被投影到图像2中的点x’和e’，即

• $x\'=P\'P^+ x$
• $e\'=P\'C$

从而，图像1中的点x的对极线即为

l′=e′×x′=P′C×P′P+x=[P′C]×P′P+对极几何

多视图几何（基础矩阵和照相机矩阵原理）

对极几何

对极几何基本概念

对极几何的理解和原理推导

多视几何：摄像机模型的推导