《数值分析》-- 埃尔米特插值与分段插值
Posted 胜天半月子
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了《数值分析》-- 埃尔米特插值与分段插值相关的知识,希望对你有一定的参考价值。
一、埃尔米特插值
-
问题
在实际问题中,对所构造的插值多项式,不仅要求函数值重合,而且要求导数也重合。
即:要求插值函数 P ( x ) P(x) P(x) 满足: P ( x i ) P(x_i) P(xi) = f ( x i ) f(x_i) f(xi), P ‘ ( x i ) P^`(x_i) P‘(xi) = f ‘ ( x i ) f`(x_i) f‘(xi), i = 1 , 2 , . . . , n i=1,2,...,n i=1,2,...,n
把此类插值多项式称为埃尔米特(Hermite)插值多项式或称带导数的插值多项式,记为 H ( x ) H (x) H(x)。
H ( x ) H (x) H(x) 存在且唯一 -
实例分析




习题
二、分段插值
2.1 龙格现象
一般总认为多项式插值函数
L
n
(
x
)
L_n(x)
Ln(x)的次数n越高逼近被插
f
(
x
)
f_(x)
f(x)的精度越好,但实际上并非如此。这是因为对任意的插值节点,当n→∞时,
L
n
(
x
)
L_n(x)
Ln(x)不一定收敛于
f
(
x
)
f_(x)
f(x)。
20世纪初龙格(Runge)就给了一个等距节点插值多项式
L
n
(
x
)
L_n(x)
Ln(x)不收敛于
f
(
x
)
f_(x)
f(x)的例子
高次插值可能会使插值误差増大

- 实例解析

2.2 分段线性插值
分段线性插值就是通过插值点用折线段连接起
来逼近
f
(
x
)
f(x)
f(x).

通过定义我们了解到:

- 给定区间
[
a
,
b
]
[a,b]
[a,b]划分:
a
=
x
0
<
x
1
<
.
.
.
<
x
n
=
b
a=x_0<x_1<...<x_n =b
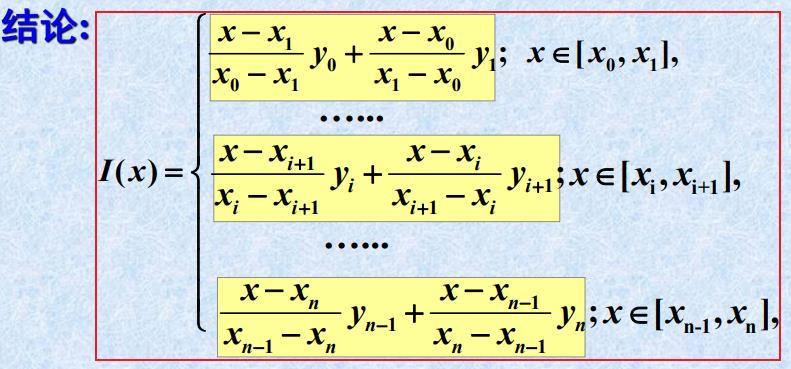
a=x0<x1<...<xn=b,如何求解分段线性插值多项式
I
(
x
)
I(x)
I(x)?
- 误差估计⭐
- 定理
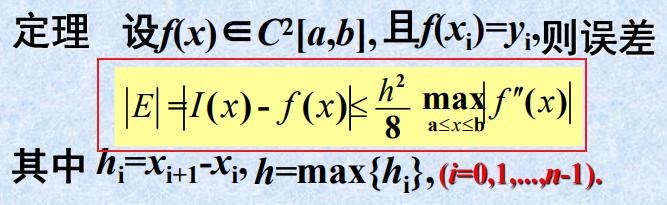
- 证明
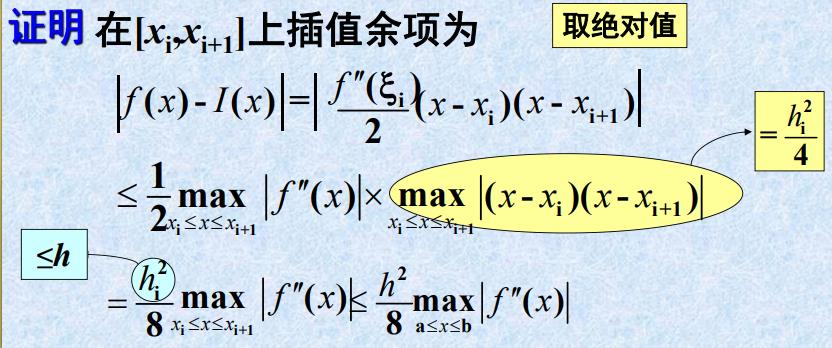
习题 - 分段线性插值的缺点
分段线性插值在节点处不可导,光滑性差
2.3 分段三次Hermite插值
分段线性插值:计算量小,误差为
O
(
h
2
)
O(h^2)
O(h2).
缺点:在节点处不可导, 光滑性差.
-
问题

-
解决


-
误差


习题
-
例题
- 求
f
(
x
)
f(x)
f(x)=
x
4
x^4
x4在[
x
i
x_i
xi,
x
i
x_i
xi
+
_+
+
1
_1
1]的3次Hermite插值多项式

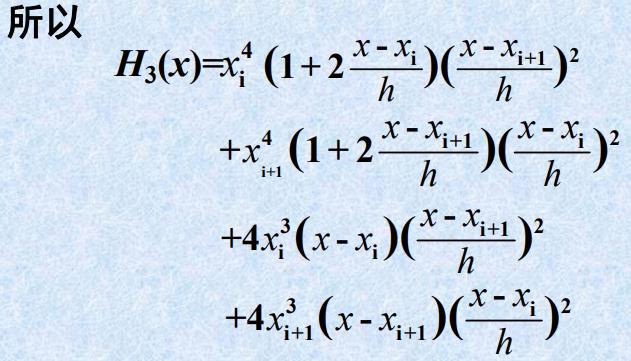
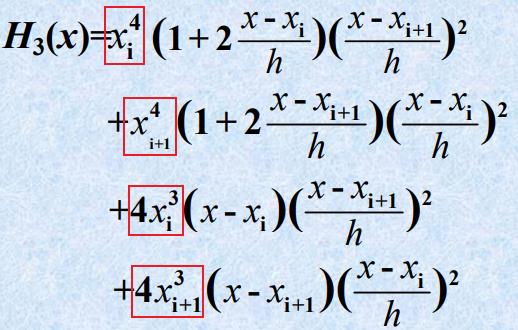

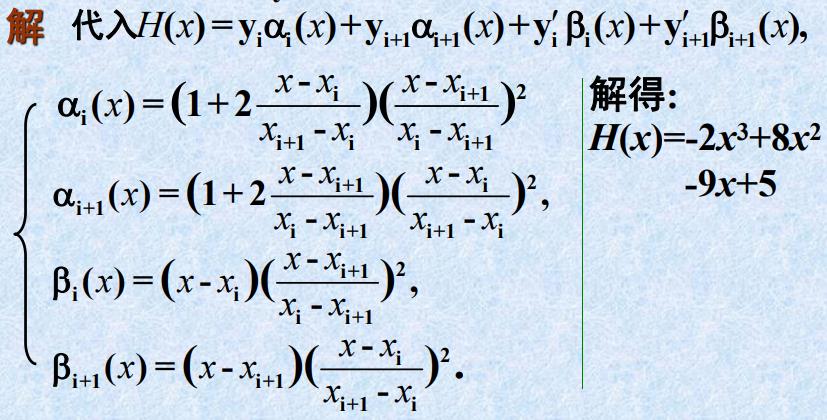
- 例题
- 解析

总结
以上是关于《数值分析》-- 埃尔米特插值与分段插值的主要内容,如果未能解决你的问题,请参考以下文章
