数值分析-插值法

Posted 2021-01-11 shensobaolibin

我们能得到一个函数f在区间[a,b]上某些点的值或者这些点上的高阶导数

我们就能通过插值法去得到一个函数g，g与f是非常相近的

一般来说g分为三类，一类是n次多项式 a_n*xⁿ + a_n-1*x^n-1 + .......+a₀，一类是三角多项式，最后一类是分段n次多项式

 

多项式插值

这个可以说是最简单的插值了

 对于a_n*xⁿ + a_n-1*x^n-1 + .......+a0，我们有n+1个未知数，我只需要知道n+1个点的函数值就可以解出这n+1个未知数

将解出的值带入即可

 

优点:简单粗暴

缺点:要解n+1个方程，时间复杂度较高，n不好确定，若n过大，容易过拟合，若n过小，容易欠拟合

 

拉格朗日插值

先说一阶多项式

我们有两点式

f(x) = y_k*(x_k+1 - x) / (x_k-x_k+1) + y_k+1*(x-x_k) / (x_k+1 - x_k) 

此两点式可以看做? * y_k + (1-?) * y_k+1

那么自然的在x=x_k的时候 ?=0  在x=x_k+1的时候?=1

这里的?其实是与x相关的一阶多项式

再说二阶多项式

对于一个二次函数，我们有三个点(x_k-1,y_k-1) ,(x_k,y_k) ,(x_k+1,y_k+1)

我们有l_k-1,l_k,l_k+1

f(x) = l_k-1*y_k-1 + l_k*y_k  +  l_k+1*y_k+1

其中l是与x相关的二次多项式

我们可以把l当作基函数

这样的话就有

x = x_k-1 时l_k-1 = 1, l_k=0, l_k+1 = 0

x = x_k时   l_k-1 = 0, l_k=1, l_k+1 = 0

x = x_k+1时l_k-1 = 0, l_k=0, l_k+1 = 1

那么这个插值基函数是很好求的

因为每个插值函数都有两个零点

对于l_k-1来说有零点x_k,x_k+1

那么lk-1就可以表示为l_k-1 = A*(x-x_k)*(x-x_k+1)

因为x=xk-1时l_k-1 = 1

所以A = 1 / (（x_k-1 - x_k）* (x_k-1 - x_k+1) )

那么同理l_k和l_k+1也能求出来了

那我们得到二阶的拉格朗日插值多项式

 

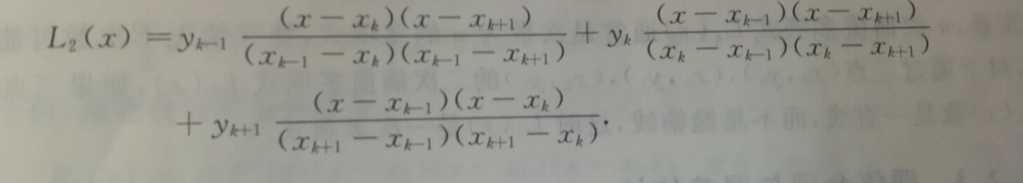
现在将二阶推广到n阶

得到n接的拉格朗日插值多项式

 

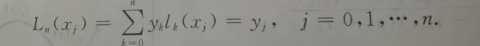
优点:算法较为简单

缺点:暂不清楚