机器学习笔记：高斯判别分析

Posted 2021-12-22 UQI-LIUWJ

1 模型概述

假设有如下数据：

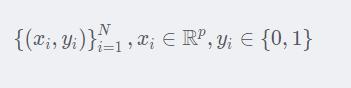
其中样本数据的类别y在给定的情况下服从伯努利分布

 不同类别的样本数据又分别服从不同的多元高斯分布（这里假设两个高斯分布具有同样的方差）

 2 损失函数

高斯判别模型的损失函数为其log似然，要估计的参数θ为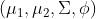

 然后用极大似然估计

3 参数估计

为了方便起见， 定义标签为1的样本个数为N1，标签为0的样本个数为N2，则有N1+N2=N

3.1 估计 Φ

ϕ只存在于③式中，因此求解ϕ只需要看③式即可：

 3.2 求解μ1

μ1只存在于①式中，因此求解μ1只需要看①式即可：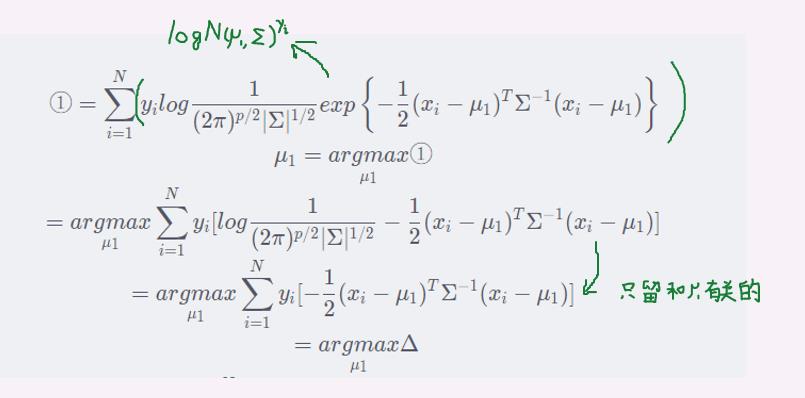

 

 

 3.3 求解μ2

求解μ2和μ1 类似

3.4 求解Σ

我们令

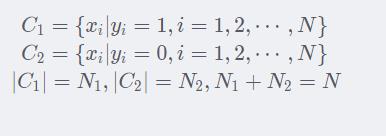
 和Σ有关的是①和②：

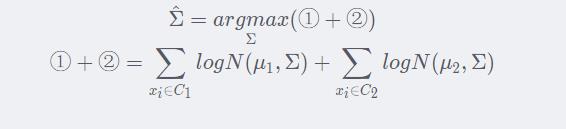
 先看通项

 

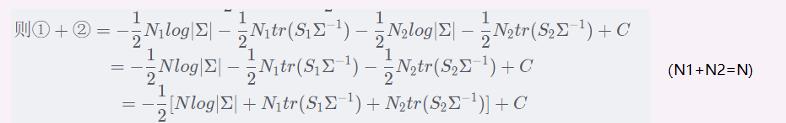
 导数为0，于是有：

在线性代数笔记：标量、向量、矩阵求导_UQI-LIUWJ的博客-CSDN博客 中，我们有：

 

 于是

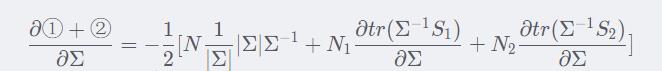
两边同时左乘&右乘一个 ，有： 

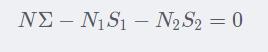
即：

4 总结 

对于一组样本数据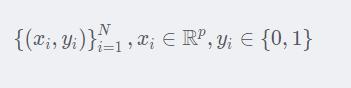 

当我们知道样本数据的类别y在给定的情况下服从伯努利分布，

同时不同类别的样本数据又分别服从不同的多元高斯分布（这里假设两个高斯分布具有同样的方差）时

 

y落入分类1的概率Φ为，即属于分类1的y的占比

属于分类1的x的均值为：，即属于分类1的那些xi向量的均值

属于分类0的x的均值为：，即属于分类0的那些xi向量的均值

不同分类的x的协方差为：即属于分类1和0的向量xi的协方差的平均

参考资料：机器学习-白板推导系列笔记（四）-线性分类_scu-liu的博客-CSDN博客