[人工智能-深度学习-52]:RNN的缺陷与LSTM的解决之道
Posted 文火冰糖的硅基工坊
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[人工智能-深度学习-52]:RNN的缺陷与LSTM的解决之道相关的知识,希望对你有一定的参考价值。
作者主页(文火冰糖的硅基工坊):文火冰糖(王文兵)的博客_文火冰糖的硅基工坊_CSDN博客
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/121547541
目录
1.4 梯度弥散/消失(每天堕落一点点,N天后,你就彻底完蛋)
第1章 RNN的缺陷
1.1 RNN的前向过程
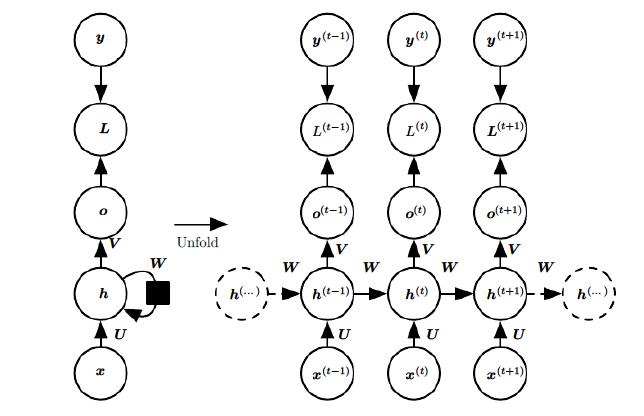
1.2 RNN反向求梯度过程
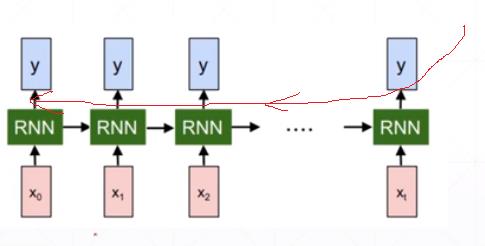
BPTT(back-propagation through time)算法是常用的训练RNN的方法,其实本质还是BP算法,只不过RNN处理时间序列数据,所以要基于时间反向传播,故叫随时间反向传播。
BPTT的中心思想和BP算法相同,沿着需要优化的参数的负梯度方向不断寻找更优的点直至收敛。综上所述,BPTT算法本质还是BP算法,BP算法本质还是梯度下降法,那么求各个参数的梯度便成了此算法的核心。
可以观察到,在某个时刻的对W或是U的偏导数,需要追溯这个时刻之前所有时刻的信息,这还仅仅是一个时刻的偏导数,上面说过损失也是会累加的,那么整个损失函数对W和U的偏导数将会非常繁琐。虽然如此但好在规律还是有迹可循,我们根据上面两个式子可以写出L在t时刻对W和U偏导数的通式:

整体的偏导公式就是将其按时刻再一一加起来。
前面说过激活函数是嵌套在里面的,如果我们把激活函数放进去,拿出中间累乘的那部分:

另一种表述方法:
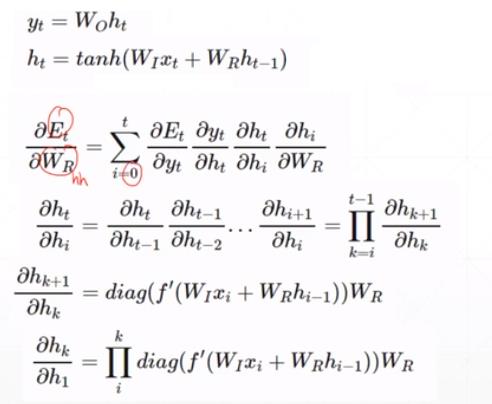
我们会发现累乘会导致激活函数导数的累乘,进而会导致“梯度消失“和“梯度爆炸“现象的发生。
1.3 梯度爆炸(每天进一步一点点,N天后,你就会腾飞)

只要每一级的梯度都大于1,则经过N轮(比如N=365), 最后的梯度就会非常大。
应对梯度爆炸的方法很简单:
只要在进行梯度迭代时,对迭代的梯度进行检查,如果大于某个数值,就把迭代的梯度现在在某个值范围内。
注意:这里限制的是:每次迭代时的梯度的值,而不是参数W的值。
1.4 梯度弥散/消失(每天堕落一点点,N天后,你就彻底完蛋)
只要每一级的梯度都小于1,则经过N轮(比如N=365), 最后的梯度会为0。

1.5 RNN网络梯度消失的原因
这是sigmoid函数的函数图和导数图。

这是tanh函数的函数图和导数图。
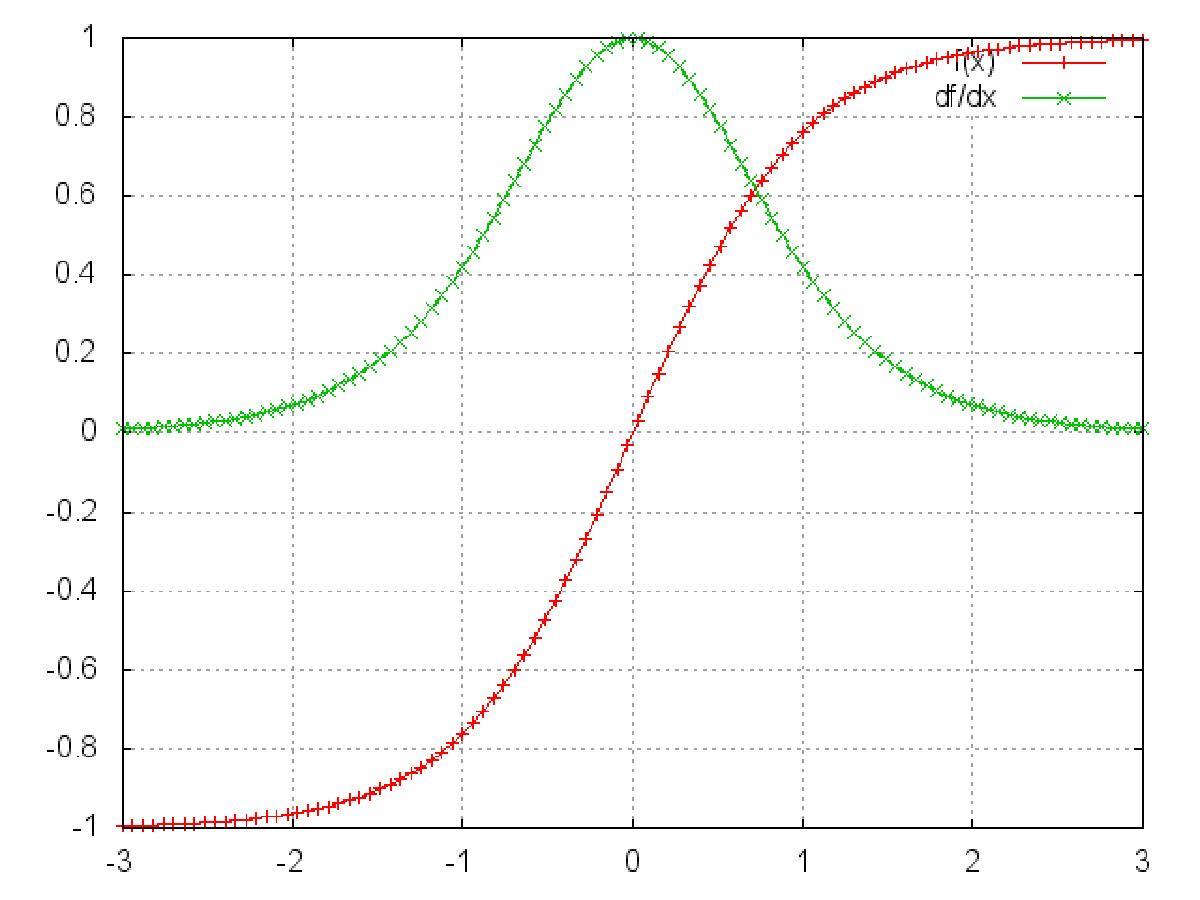
它们二者是何其的相似,都把输出压缩在了一个范围之内。他们的导数图像也非常相近,我们可以从中观察到,sigmoid函数的导数范围是(0,0.25],tach函数的导数范围是(0,1],他们的导数最大都不大于1。
这就会导致一个问题,在上面式子累乘的过程中,如果取sigmoid函数作为激活函数的话,那么必然是一堆小数在做乘法,结果就是越乘越小。随着时间序列的不断深入,小数的累乘就会导致梯度越来越小直到接近于0,这就是“梯度消失“现象。
其实RNN的时间序列与深层神经网络很像,在较为深层的神经网络中使用sigmoid函数做激活函数也会导致反向传播时梯度消失,梯度消失就意味消失那一层的参数再也不更新,那么那一层隐层就变成了单纯的映射层,毫无意义了,所以在深层神经网络中,有时候多加神经元数量可能会比增加深度好。
你可能会提出异议,RNN明明与深层神经网络不同,RNN的参数都是共享的,而且某时刻的梯度是此时刻和之前时刻的累加,即使传不到最深处那浅层也是有梯度的。这当然是对的,但如果我们根据有限层的梯度来更新更多层的共享的参数一定会出现问题的,因为将有限的信息来作为寻优根据必定不会找到所有信息的最优解。
之前说过我们多用tanh函数作为激活函数,那tanh函数的导数最大也才1啊,而且又不可能所有值都取到1,那相当于还是一堆小数在累乘,还是会出现“梯度消失“,那为什么还要用它做激活函数呢?原因是tanh函数相对于sigmoid函数来说梯度较大,收敛速度更快且引起梯度消失更慢。
还有一个原因是sigmoid函数还有一个缺点,Sigmoid函数输出不是零中心对称。sigmoid的输出均大于0,这就使得输出不是0均值,称为偏移现象,这将导致后一层的神经元将上一层输出的非0均值的信号作为输入。关于原点对称的输入和中心对称的输出,网络会收敛地更好。
RNN的特点本来就是能“追根溯源“利用历史数据,现在告诉我可利用的历史数据竟然是有限的,这就令人非常难受,解决“梯度消失“是非常必要的。
1.6 解决“梯度消失“的方法主要有:
(1)选取更好的激活函数
一般选用ReLU函数作为激活函数,ReLU函数的图像为:

ReLU函数的左侧导数为0,右侧导数恒为1,这就避免了“梯度消失“的发生。
但恒为1的导数容易导致“梯度爆炸“,但设定合适的阈值可以解决这个问题。还有一点就是如果左侧横为0的导数有可能导致把神经元学死,不过设置合适的步长(学习旅)也可以有效避免这个问题的发生。
(2)改变传播结构
LSTM网络就是通过改变网络结构来缓解梯度消失的情形。
1.7 RNN网络的功能缺陷
(1)无法支持长时间序列
RNN由于梯度消失,导致RNN网络的时间序列不能太长,因此,RNN网络只能有短期记忆, 无法支持常序列的记忆。
这就意味着RNN网络,可能只能处理短句,无法处理又长篇文字组成的长文序列。
虽然,RNN网络结构看起来是支持长文的。
这就需要一种新的网络结构来支持长时间的序列输入。
所谓无法记住“长序列”, 只能记住“短”时上下文,是指“长序列”梯度的消失。

“红烧排骨”出现在文字的开头,当输入到最后字符串是,RNN网络,可能已经忘记了本序列最重要的单词“红烧排骨”,.....的做法与辣子鸡相似,最后就有可能预测出“辣子鸡”。
(2)RNN网络不同词对当前输出的影响效果完全取决于“时间”
RNN网络,在时间是是串联关系,离当前时间越远的隐藏层的输出,对当前隐藏层的输出的影响越小。RNN无法根据不同词本身的重要性来对当前的输出产生影响 。
(3)RNN网络对所有序列输入是平等对待
RNN对所有输入具有同等的特征提取的能力,对于一句话中的所有单词,都会提取他们的特征 ,并作为下一特征的输入。也就是说RRN网络,记住了所有的信息,并没有区分哪些是有用信息,有哪些是无用信息,哪些是辅助信息。
然而,实际语言文字中,不同单词虽然有特征,但对目标的作用是不同的,有些词,对于最终的目标,其实没有任何意义,就是修饰词而已。而有些词的特征,起着决定性对的作用,这些词,就需要通篇文章范围内进行记忆,也就是说,不同词的重要性,不仅仅取决于词之间的物理距离,而且取决于词本身的意义。
这就需要一种网络,能够根据词的重要性有选择性的进行丢弃和记忆。
丢弃无效信息、记住有效信息的好处是:
- 输入序列就可以变长,不容易出现梯度消失
- 使得有效信息即使离当前输入距离较远,也能够产生较大的影响力。
- 实现长期记忆

能够满足上述功能的网络就是RNN网络的升级版本, LSTM网络。
第2章 LSTM长短期记忆网络
2.1 LSTM概述
LSTM(long short-term memory)。
长短期记忆网络是RNN的一种变体,LSTM网络通过精妙的门控制将短期记忆与长期记忆结合起来,并且一定程度上解决了梯度消失的问题。
LSTM 由Hochreiter & Schmidhuber 早在1997年就提出,后来被Alex Graves进行了改良和推广后,在很多问题的解决上,LSTM 都取得相当巨大的成功,因此在处理序列输入的场景中得到了广泛的使用。
LSTM 通过刻意的设计的基本组成单元Cell来实现长期记忆的功能的。

2.2 RNN的单元结构
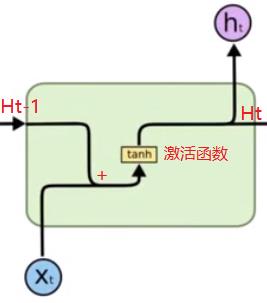
在该结构中,只有一个记忆状态Ht-1,该记忆信息与当前的输入信息一起,产生一个新的记忆状态Ht。
所谓记忆,这里就是Ht-1、Ht的值。而H对应的权重矩阵,就是对记忆的提取。
所谓当前的输入,就是Xt。而与Xt对应的权重矩阵,就是瞬时记忆。
在这里,
- Ht-1是所有历史输入的记忆汇总,即无丢弃,无选择性记忆。
- 历史输入离当前的时间越远,对当前输出Ht的影响越小,即长期记忆被遗忘。
而Ht = Tanh(Xt*Wx + Ht-1 * Wh), 是历史记忆+瞬时记忆产生新的记忆。
2.3 LSTM网络的基本组成单元:Cell
记住长期的信息在实践中是 LSTM 网络天然的、默认能力,而非需要付出很大计算或内存代价才能获得的能力。这得益于LSTM独特的Cell结构,即LSTM网络的基本组成单元。
LSTM的Cell是一个具备选择性记忆功能的记忆单元。

(1)信息流的走向:
- 本轮时序信息输入:Xt
- 输入合并:Xt首先与当前的短时记忆Ht-1进行合并,得到(X, Ht-1)
- 遗忘门sigmod函数开关:通过Wf矩阵和(X, Ht-1),确定本轮的输出是否需要使用到长时记忆,以及使用多大程度的长时记忆Ct-1, sigmod的输出在[0, 1]之间。
- 产生本轮新信息:通过W矩阵和(X, Ht-1)以及tanh函数,产生本轮的新信息~Ct。
- 输入门sigmod开关:通过Wi矩阵和(X, Ht-1),确实是否把本次产生的新信息~Ct,叠加到长时记忆Ct-1中,以及多大程度的使用本次的新信息, sigmod的输出在[0, 1]之间。
- 产生新的长时记忆:上一时刻的长时记忆Ct-1与本次提取的新信息~Ct进行叠加, 得到Ct = Ct-1 + ~Ct。
- 产生本轮的输出:通过Wo矩阵和Ct以及tanh函数,产生本轮的输出信息~Ht-1
- 输出门sigmod开关:通过Wq矩阵和(X, Ht-1),确实是否需要把本轮产生的输出~Ht-1, 作为短时记忆保存到Ht中。
- 本轮的时序信息输出:Ht 与 Ct
(2)LSTM的两个状态 - 外部接口
RNN只有一个隐藏状态(记忆信息)在相邻单元之间传递。
LSTM具备两个状态信息(记忆信息)在两个相邻单元之间传递。
- 一个长时记忆Ct,
- 一是上一时刻的短时记忆Ht(瞬时记忆)
(3)特殊的内部结构
RNN内部只有一个加分运算和激活函数
LSTM内部结构包括:
- sigmod激活函数,起着模拟开关的作用,或称为记忆强度,0表示完全遗忘,1表示完全记忆,0-1表示部分记忆。

- 三个乘法:乘法与sigmod函数一起,起着三个“门控”的作用。与0相乘为0(关闭、遗忘),与1相乘等于输入(打开、记忆)。
- 一个加法:完成当前的瞬时输入Xt、短时记忆Ht-1、长时记忆Ct-1三者的输出。
- 一个tanh激活函数:为当期输出所需的激活函数。
(4)LSTM的三个门
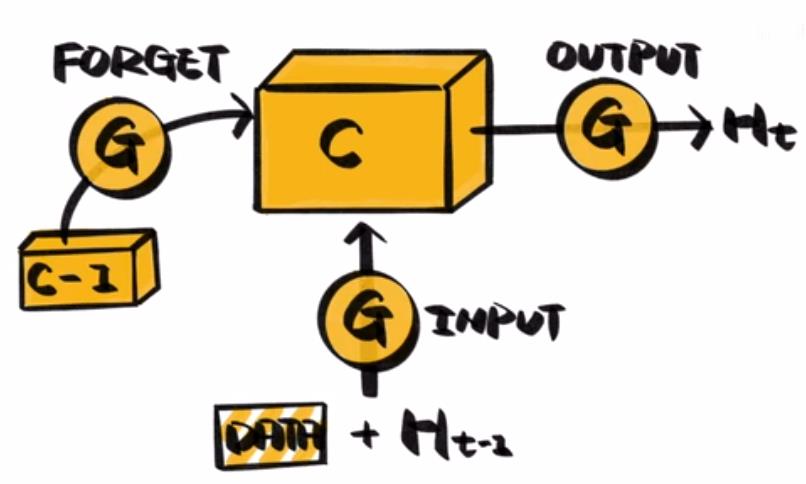
- Forget门,遗忘门,也就是第一个sigmod函数:它决定在当期的状态一下以及当期的输入请下下,即本次迭代输出,需要使用多大比例的之前的长期记忆。
- 输入门,也就是第二个sigmod函数:决定了本次迭代的输出有多少需要保存到小盒子的长期记忆中,也就是说,需要记住哪些新内容。通过输入门,了解当前网络的输入信息。
- 输出门,而就是第三个sigmod函数:决定来了多大程度的输出长期记忆小盒子中的信息。
2.4 LSTM网络组成单元的数学表达式
(1)Xt与Ht-1的合并
[Ht-1, Xt] = concatenate(Ht-1, Xt)
[Ht-1, Xt]是后续所有控制门和新信息产生的输入数据。
(2)遗忘门的数学公式
遗忘门是表示我们希望什么样的信息进行保留,什么样的信息可以通过,所以这里的激活函数是sigmoid。

(3)输入门
用sigmoid建立一个输入门层,决定什么值我们将要更新,接着用tanh建立一个候选值向量,并将其加入到状态中。
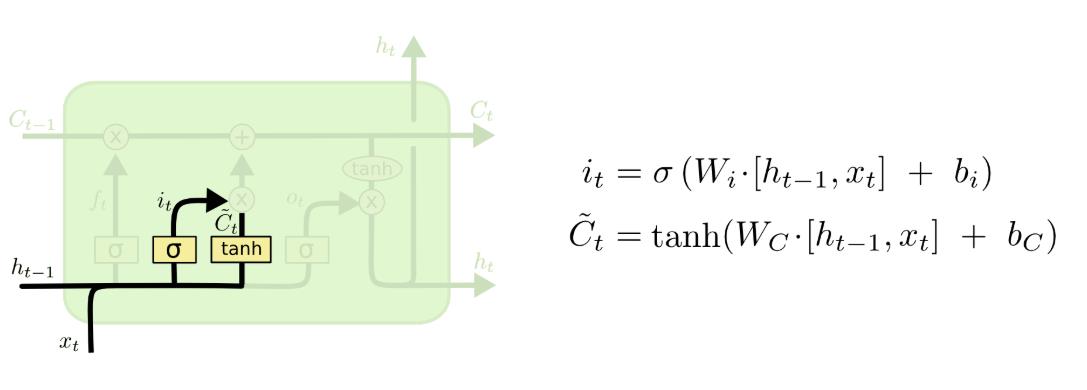
上图,除了输出门的数学表达式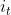 外,还包括本轮新信息产生的数学表达式~Ct。
外,还包括本轮新信息产生的数学表达式~Ct。
~Ct通过输入门,最终与长时记忆,Ct-1进行叠加(Add), 新的长时记忆Ct, 即Ct = Ct-1 * 遗忘门门控值 + ~Ct * 输入门门控值,即为:
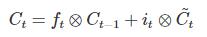
(4)输出门
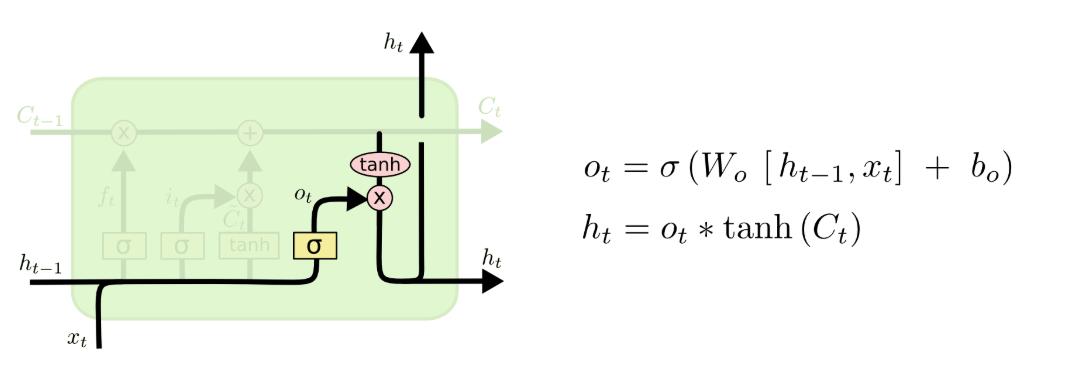
上图,除了输出门的数学表达式 外,还包括本轮的最终输出Ht。
外,还包括本轮的最终输出Ht。
2.5 数学表达值汇总
(1)两个输入
[Ht-1, Xt] = concatenate(Ht-1, Xt)
(2)两个输出

(3)中间单元

第3章 LSTM网络结构
3.1 RNN网络的串联结构
所有 RNN 都具有一种重复神经网络模块的链式的形式。在标准的 RNN 中,这个重复的模块只有一个非常简单的结构,例如一个 tanh 层。
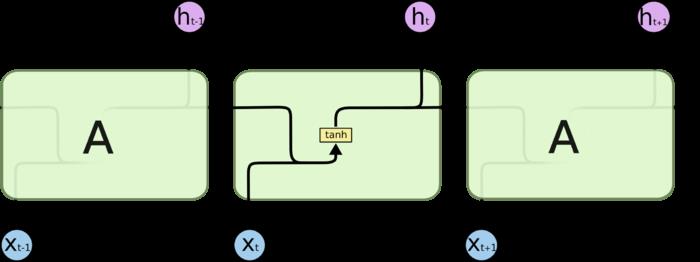
3.2 LSTM网络的串联结构
LSTM 同样是这样的结构,只是重复的模块拥有一个不同的结构。
不同于单一神经网络层,整体上除了h在随时间流动,细胞状态c也在随时间流动,细胞状态c就代表着长期记忆。

作者主页(文火冰糖的硅基工坊):文火冰糖(王文兵)的博客_文火冰糖的硅基工坊_CSDN博客
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/121547541
以上是关于[人工智能-深度学习-52]:RNN的缺陷与LSTM的解决之道的主要内容,如果未能解决你的问题,请参考以下文章
[人工智能-深度学习-47]:卷积神经网CNN+循环神经网络RNN与组合电路+时序电路的比较
原创 [人工智能-深度学习-48]:RNN是循环神经网络还是递归神经网络?