[人工智能-深度学习-51]:循环神经网络RNN基本原理详解
Posted 文火冰糖的硅基工坊
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[人工智能-深度学习-51]:循环神经网络RNN基本原理详解相关的知识,希望对你有一定的参考价值。
作者主页(文火冰糖的硅基工坊):文火冰糖(王文兵)的博客_文火冰糖的硅基工坊_CSDN博客
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/121387285
目录
5.1 前向计算/预测: 隐藏层的数学公式(Elman网络)
5.2 循环神经网络的工作原理 - 反向计算:训练 =>BPTT算法
第1章 详解前的铺垫
1.1 组合逻辑 VS 时序逻辑
1.2 循环神经网络 VS 递推神经网络
1.3 RNN的主要应用场景
第2章 循环神经网络RNN的结构 - 个人理解
2.1 “非时序”的组合单元的网络结构
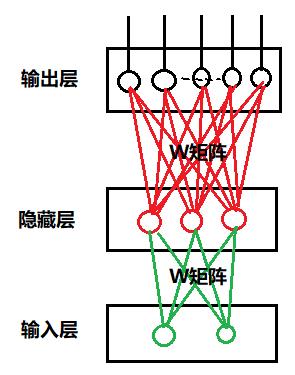
上图的案例是:“非时序”单元的网络结构,即“组合”逻辑的网络结构。
在上图案例中:
- 输入层的输入特征的维度为:1 * 2
- 输入层的W矩阵的维度为: 2 * 3
- 隐藏层输出特征的维度为 1 * 3 = (1 * 2)X ( 2 * 3)
- 输出层的W矩阵的维度为: 3 * 5
- 输出层输出特征的维度为: 1 * 5 =(1 * 3)x ( 3 * 5)
2.2 RNN基本的结构:“时序”单元
(1)内部结构
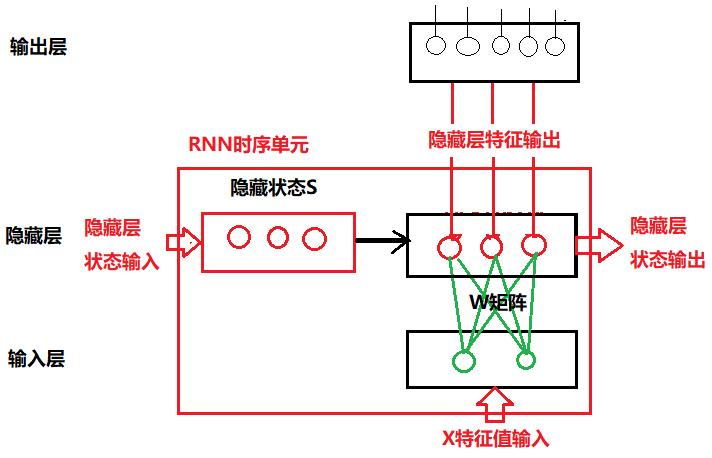
相对于“组合”网络,“时序”网络多出来的逻辑包括:
- 内部的隐藏状态S(与X一起,作为隐藏层神经元的输入),通常通过张量Tensor来保存。
- 内部的隐藏状态的输入张量与隐藏层神经元之间的连接:W矩阵。
- 内部的隐藏状态S的输入(前一时刻T0)
- 内部的隐藏状态S的输出(当前时刻T1)
(2)等效结构
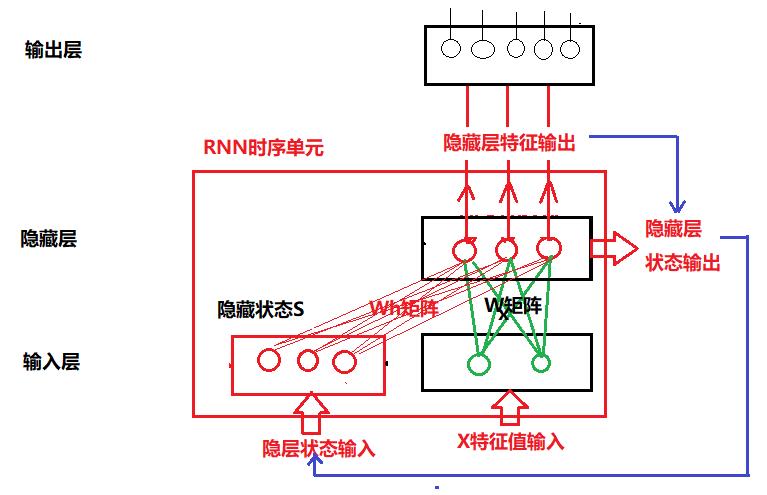
与组合电路不同的是,RNN网络(不包括输出层)包括了两个输入,两个输出,两个权重矩阵,一组神经元。
- 输入:用于保存输入特征的张量/向量X:(X1,X2...Xn)=》同“组合”单元 ,假设形状为 1 * N =》同“组合”单元
- 输入:上一次前向运算时的隐层输出S =》“时序”单元新增
- 神经元:用于隐藏层处理/运算的神经元: (H1, H2, ...Hm) =》同“组合”单元。
- 输出:前向计算的输出, 假设其形状为 1 * M =》同“组合”单元
- 输出:隐层的输出 =》 “时序”单元新增, 该输入,既作为输出层的输入,同时也作为RNN网络的输出。
- W权重矩阵:X特征向量与隐藏层神经元构成的权重矩阵,有时候称为Wx矩阵,又时候称为U矩阵, 则U矩阵的形状为: N * M.
- W权重矩阵:隐藏层内部状态向量或张量与隐藏层神经元构成的权重矩阵,有时候称为Wh矩阵, 有时候也简称为W矩阵, 则该矩阵的形状为 M * M!!! 见上图。
备注:
- 上文中,“红色”标注的部分,都是“时序”单元新增加的内容。
- 隐藏状态S的形状、RNN隐藏层的输出、隐藏层的特征数是一致的、相等的, 都为 1 * M
(3)RNN网络的两种类型
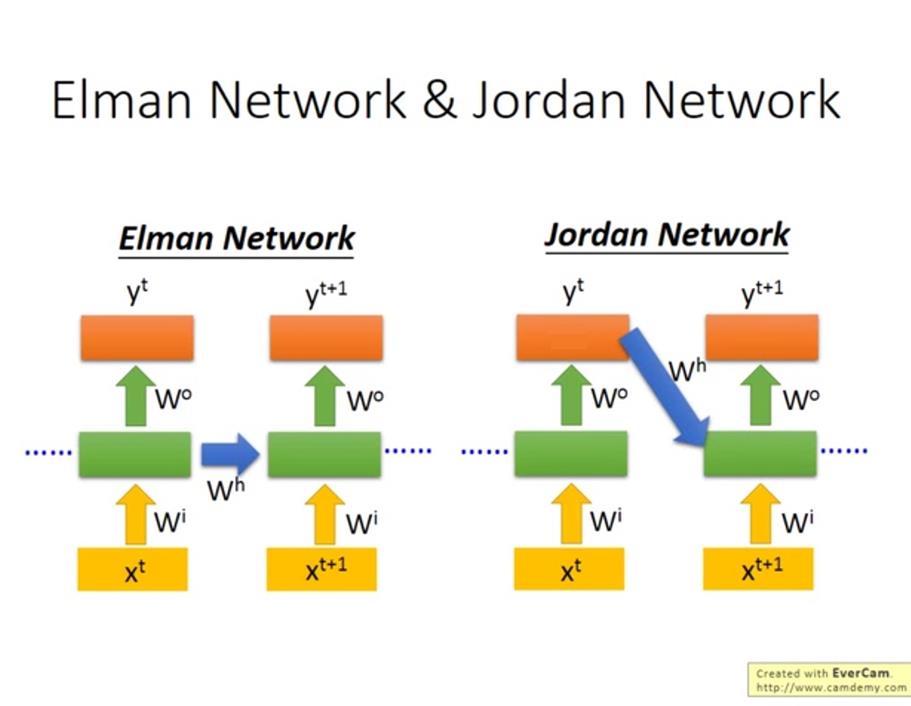
- Elman network:是一个隐藏层的输出Hi经过时延后作为下一时刻这一层的输入的一部分,然后recurrent层的输出同时送到网络后续的层,比如最终的输入层。
- Jordan network:直接把整个网络最终的输出Yi(i.e. 输出层的输出)经过时延后反馈回网络的输入层。
现在一般说的RNN(包括LSTM、GRU等等)都是用Elman network
2.3 “循环”的含义:网络结构对循环的支持

循环神经网络的核心是“循环”!讲清楚“循环”的含义和实现,才能真正的理解循环神经网络。
把T时刻的隐藏层的输出,作为T + 1时刻的隐藏状态S的输入,就构成了上图中的蓝色的“循环线”。
2.4 “循环”的含义:循环的实施
蓝色的循环线,到底如何实现呢?
是RNN神经网络自身来实现“循环”?
还是由RNN网络外部的使用者来实现“循环”呢?
其实RNN网络本身并没有对此作出限制,这两种形式或方式都有:
(1)压缩/单体结构:RNN网络的使用者实现串联
(2)展开/串联结构: RNN网络自身实现串联
2.5 RNN的压缩结构:由外部的RNN网络的使用者来实现“循环”
(1)网络的基本结构
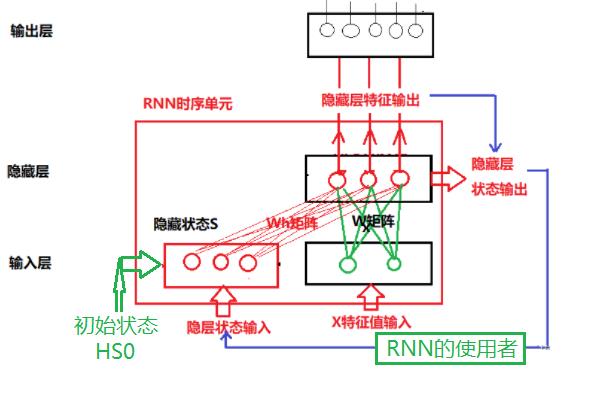
(2)时间序列输入的实现流程
在这种模式下,RNN的使用者,负责读取T时刻的隐层状态的输出,并在T+1时刻,把T时刻的状态值作为隐层状态S, 与T+1时刻的X一起,作为隐藏层神经元的输入, 如下所示:

伪代码实现方法:
- hide_state的初始化
hide_state = 0
- T+0时刻对Xt+0进行预测:
output, hide_state = rnn.forward (Xt + 0, hide_state)
- T+1时刻对Xt+1进行预测:
output, hide_state = rnn.forward (Xt + 1, hide_state)
- T+2时刻对Xt+2进行预测:
output, hide_state = rnn.forward (Xt +2, hide_state)
(3)优点
- RNN网络的结构简单
- RNN网络本身消耗的内存小,RNN网络不需要保存整个序列历史状态的张量,只需要保存当前的历史状态hide_state。如果需要记录序列的历史状态或输出结果,则需要RNN的使用者保存。
(4)缺点
- RNN网络不能并行的处理序列输入,一次只能处理一个序列中的一个单元(如单词),如“I love china”这个序列,RNN网络一次只能处理一个单词,无法并行的处理整句话(多个单词组成的序列)。
2.6 RNN展开结构:由RNN网络自身来实现序列内的“循环”?
(1)网络的基本结构
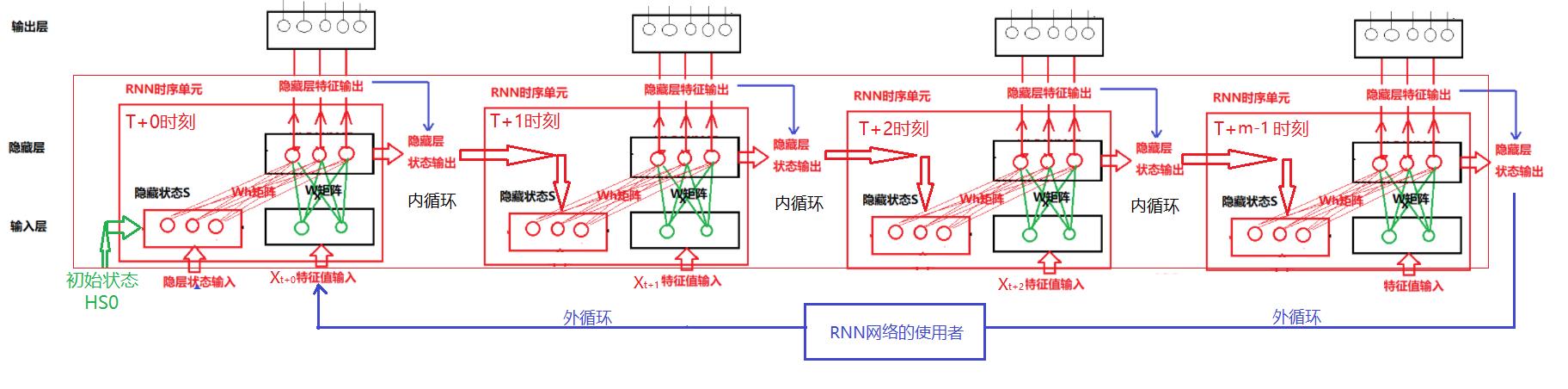
- 在这种模式下,RNN网络自身会记住长度为m的序列的中间状态(通过张量Tensor变量实现)
- 在这种模式下,RNN网络是由m个"时序"单元横向串联而成。m越大,RNN网络能够并行处理的序列的长度越长, 即等于m。
(2)时间序列输入的实现流程
当RNN网络的使用者, 其待处理的序列数据的长度Seq_len > RNN能够并行处理的序列数据的长度m时,RNN网络的使用者,负责待处理原始序列数据的分割,分割成长度为m的序列,并由它负责把长度为m的不同序列串联起来。
- hide_state的初始化
hide_state = 0
- T+0时刻, 对长度为m的序列进行预测:
output, hide_state = rnn.forward ([Xt+0, Xt+1, ...., Xt+m-1], hide_state)
- T+1时刻, 对长度为m的序列进行预测:
output, hide_state = rnn.forward ([Xt+m+0, Xt+m+1, ...., Xt+2m-1], hide_state)
- T+2时刻, 对长度为m的序列进行预测:
output, hide_state = rnn.forward ([Xt+2m+0, Xt+2m+1, ...., Xt+3m-1], hide_state)
备注:
- 长度为m序列的内部单元之间的串联由RNN网络自身负责完成。
- 长度为m序列的外部序列之间的串联由RNN的使用者负责完成。
(3)优点
- RNN网络,可以一次性处理由多个“单元”组成的输入序列,序列的长度取决于“时序”单元的个数,如一次性可以处理m个单词次组成的句子。
(4)缺点
- RNN网络需要张量保存每个“时序”单元的隐层的状态输出,要消耗用RNN网络的内存大小。
(5)特点
- 每个“时序”单元,针对不同的输入Xi,采用相同的特征提取算法。
- 每个“时序”单元的输入数据X的权重矩阵是共享的。
- 每个“时序”单元的隐层状态S的权重矩阵是共享的。
2.7 RNN的堆叠结构:
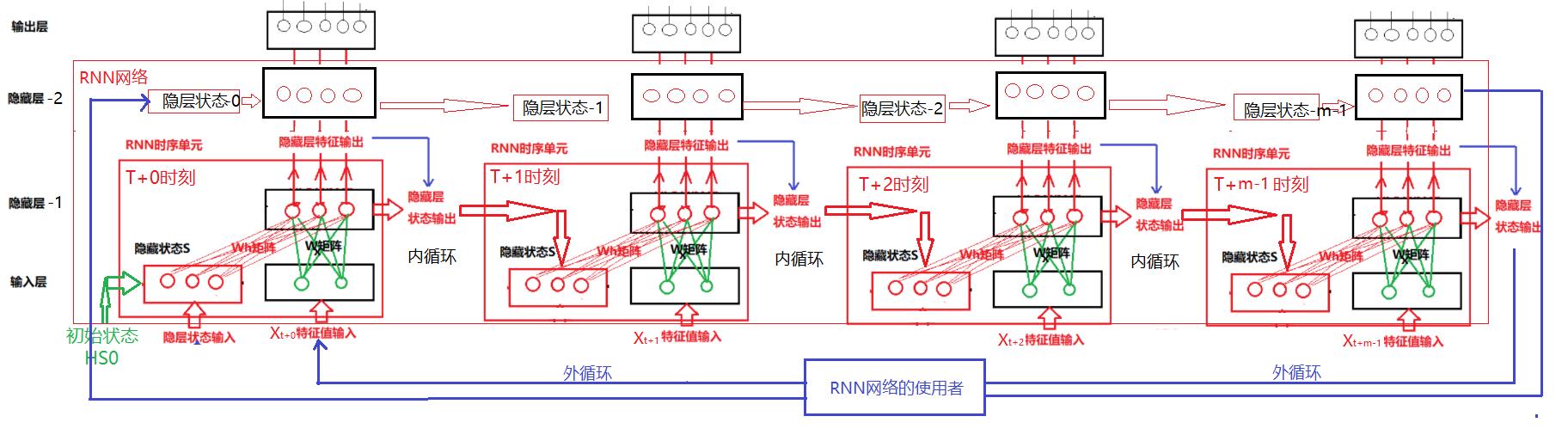
RNN堆叠是在原有隐层的基础之上,堆叠更多的隐层(不包括输入和输出层),包括其隐层状态保持器。
第3章 循环神经网络RNN的结构 - 官方定义解读
3.1 RNN的“时序”单元
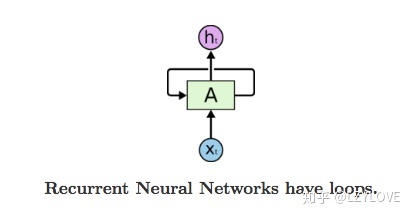
- Xt:为t时刻的样本的输入
- A: 为RNN特有的时序单元
- Ht:为t时刻,RNN时序单元的输出,即隐藏层的输出
- 循环:为t时刻的隐层的特征输出,成为t+1时刻,隐层的特征输入,与t+1时刻的样本Xt+1同时作为RNN时序单元的输入。
3.2 RNN结构的展开
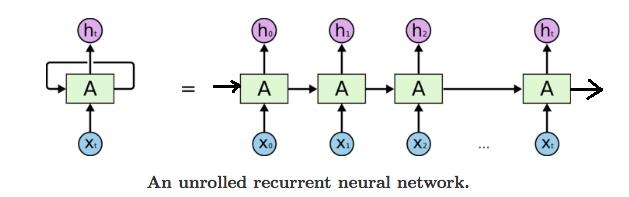
- X0, X1.....Xt:为t=0,1,2,...时刻的序列输入
- h0, h1......ht: 为t=0,1,2,...时刻的隐层输出
- A: RNN的单个时序单元,他们一次串联起来。
- 隐层的输入:送给第一个时序单元
- 隐层的输出:最后一个时序单元
3.3 RNN的叠加
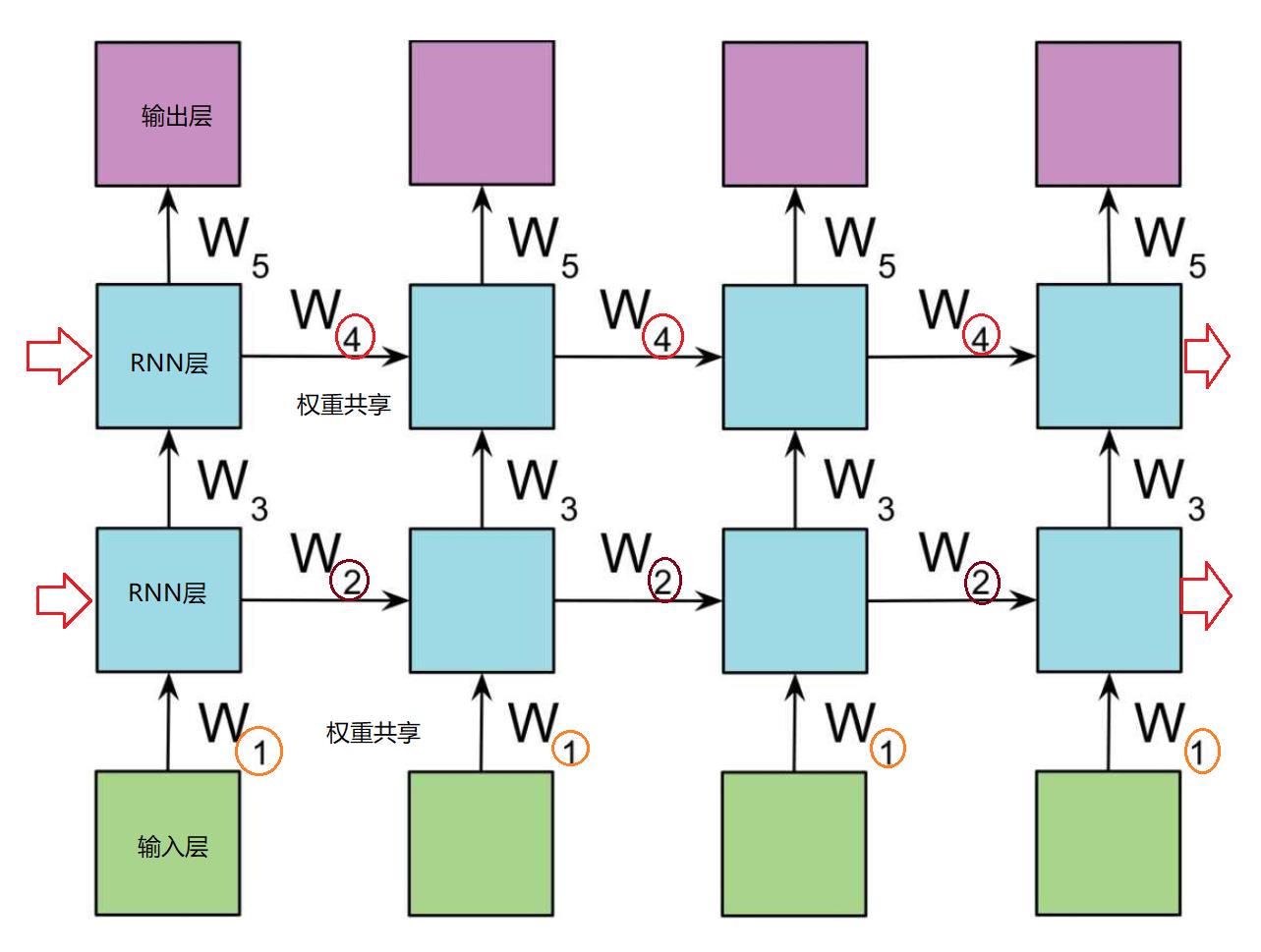
3.4 双向循环网络
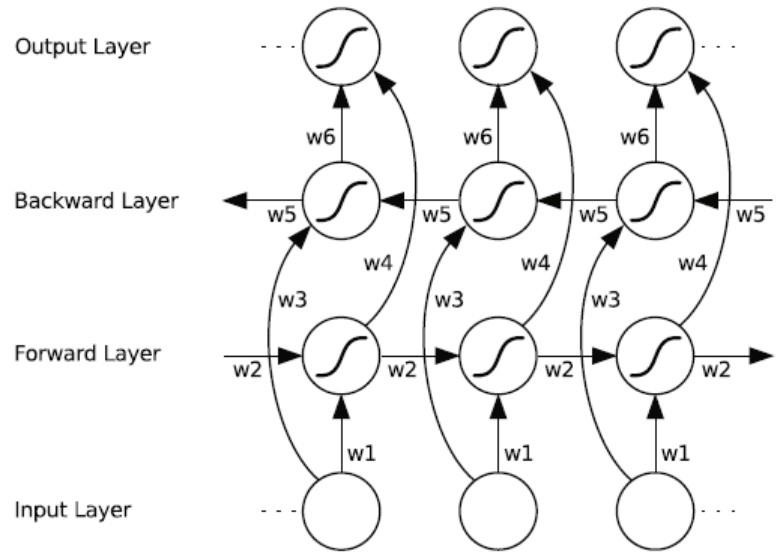
双向循环网络是两套隐层,一套为前向层,另一套是后向层,他们有独立的W矩阵和状态张量。
第4章 RNN组网
4.1 RNN网络
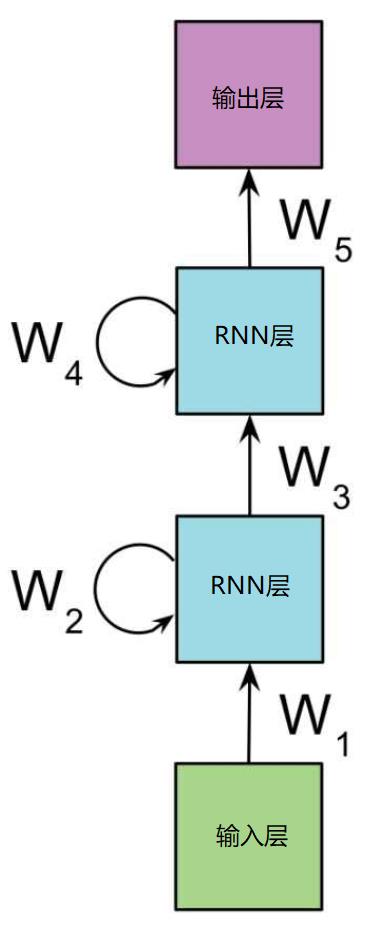
RNN与CNN类似,都是特征提取的功能,本身并不能独立组网(神经网络),还需要输入层,实现样本数据的输入。还需要输出层,完成根据特征进行分类或其他功能的输出。
4.2 RNN组网形态形态
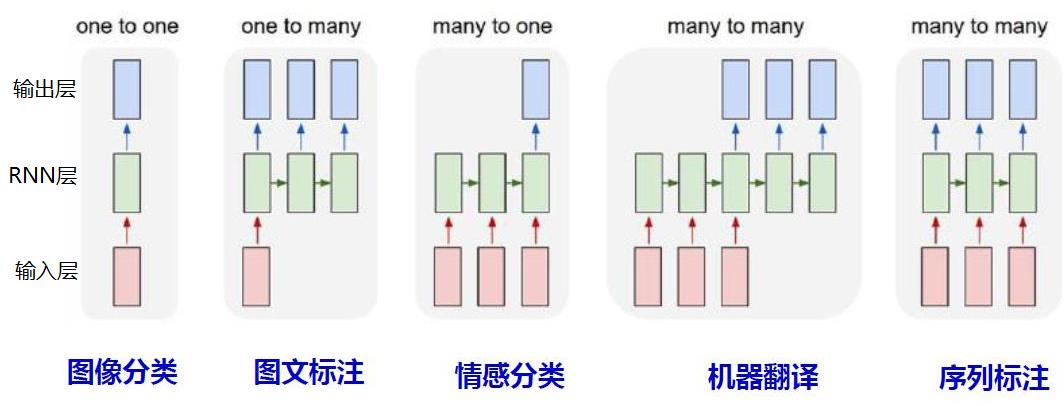
不同的组网形态,有不同的应用场景。
第5章 循环神经网络的工作原理
5.1 前向计算/预测: 隐藏层的数学公式(Elman网络)

- 激活函数:隐藏层的激活函数通常是tanh,也可以是其他函数。
- 输入样本的W矩阵:
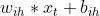
- 隐层状态的W矩阵:
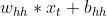
5.2 循环神经网络的工作原理 - 反向计算:训练 =>BPTT算法
有了RNN前向传播算法的基础,就容易推导出RNN反向传播算法的流程了。
RNN反向传播算法的思路和DNN(组合逻辑网络)是一样的,即通过梯度下降法一轮轮的迭代,得到合适的RNN模型参数U,W,V,b,c 。
由于我们是基于时间反向传播,所以RNN的反向传播有时也叫做BPTT(back-propagation through time)。当然这里的BPTT和DNN也有很大的不同点,即这里所有的U,W,V,b,c在序列的各个位置是共享的,反向传播时我们更新的是相同的参数。
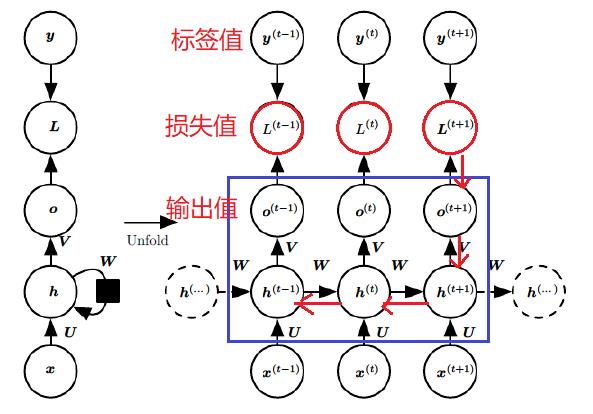
为了简化描述,这里的损失函数我们为对数损失函数,输出的激活函数为softmax函数,隐藏层的激活函数为tanh函数。
对于RNN,由于我们在序列的每个位置都有损失函数,因此最终的损失LL 为:
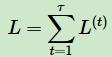
其中V,c, 的梯度计算是比较简单的:
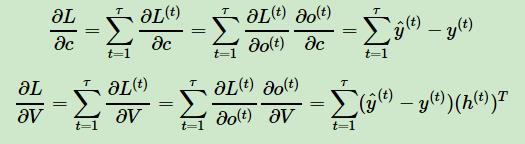
但是W,U,b 的梯度计算就比较的复杂了。从RNN的模型可以看出,在反向传播时,在在某一序列位置t的梯度损失由当前位置的输出对应的梯度损失和序列索引位置t+1t+1 时的梯度损失两部分共同决定。对于W 在某一序列位置t的梯度损失需要反向传播一步步的计算。我们定义序列索引tt 位置的隐藏状态的梯度为:
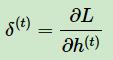
这样我们可以像DNN一样从δ(t+1) 递推δ(t)
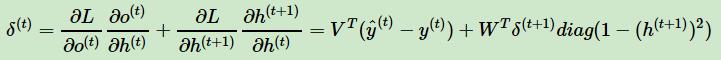
对于δ(τ) ,由于它的后面没有其他的序列索引了,因此有:
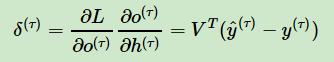
有了δ(t) ,计算W,U,b 就容易了,这里给出W,U,b 的梯度计算表达式:

参考:
(超详细!!)Pytorch循环神经网络(RNN)快速入门与实战_热爱技术,热爱生活!-CSDN博客_rnn循环神经网络
循环神经网络RNN打开手册 - 知乎 (zhihu.com)
复旦大学机器学习公开课:77-循环神经网络的训练和示例,教育,资格考试,好看视频
作者主页(文火冰糖的硅基工坊):文火冰糖(王文兵)的博客_文火冰糖的硅基工坊_CSDN博客
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/121387285
以上是关于[人工智能-深度学习-51]:循环神经网络RNN基本原理详解的主要内容,如果未能解决你的问题,请参考以下文章
 https://blog.csdn.net/HiWangWenBing/article/details/121367263
https://blog.csdn.net/HiWangWenBing/article/details/121367263