KMP算法解决字符串匹配问题(详细步骤图解)

Posted 2021-12-13 温文艾尔

KMP算法图解

文章目录

• 一、KMP算法
• • 步骤图解
• 二、部分匹配值是怎么产生的
• • 代码

---

一、KMP算法

1. KMP是一个解决模式串在文本串中是否出现过，如果出现过，最早出现的位置的经典算法
2. KMP算法常用于在一个文本串S中查找一个模式串P的出现位置，这个算法在1977年由Donald Knuth、Vaughan Pratt、James H.Morris三人发表
3. KMP算法利用之前判断过信息，通过一个next数组，保存模式串中前后最长公共子序列的长度，每次回溯时，通过next数组找到，前面匹配过的位置，省去了大量的计算时间

我们举一个例子

字符串
str1=“BBC ABCDAB ABCDABCDABDE”，
子串
str2=“ABCDABD”

利用KMP算法判断str1第一次在str2中出现的位置

步骤图解

1.首先，用str1的第一个字符和str2的第一个字符去比较，不符合，关键词向后移动一位

2.重复第一步，还是不符合，再后移

3.一直重复，直到str1有一个字符与str2的第一个字符符合为止

4.接着比较字符串和搜索词的下一个字符，还是符合

5.遇到str1有一个字符与str2对应的字符不符合

6.这时候按照传统算法，我们会继续便利str1的下一个字符，重复第一步，但是这样我们会做很多无用的工作，比如BCD我们已经判断过，已经不用再次进行判断，当空格与D不匹配时，你其实知道前面6个字符是“ABCDAB”。KMP算法的想法是：设法利用这个已知信息，不要把搜索位置移回已经比较过的位置，二十继续将他向后移，这样就提高了效率

7.我们可以对str2计算出一张部分匹配表，这表的产生在后面介绍

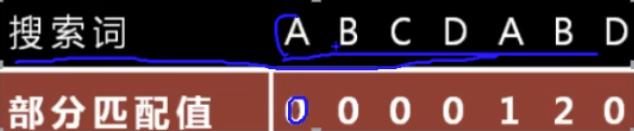
8.已知空格与0不匹配时，前面六个字符“ABCDAB”是匹配的，查表可知，最后一个匹配字符B对应的部分匹配值为2，因此按照下面的公式算出向后移动的位数：

移动位数=已匹配字符数-对应的部分匹配值，因为6-2等于4，所以将搜索词向后移动4位

9.因为空格与C不匹配，搜索词继续向后移动，这时，已匹配的字符数为2（“AB”）对应的部分匹配值为0，所以移动为数=2-0，结果为2，于是将搜索词向后移2位

10.因为空格与A不匹配，继续向后移一位

11.逐位比较，直到发现C与D不匹配，于是，移动为数=6-2，继续向后移动4位

12.逐位比较，直到搜索词的最后一位，发现完全匹配，于是搜索完成，如果还要继续搜索（即找出全部匹配），移动位数=7-0，再将搜索词向后移动7位

二、部分匹配值是怎么产生的

首先我们要了解字符串的前缀后缀

部分匹配值就是前缀和后缀的最长的共有元素的长度，以“ABCDABD为例”

1. “A”的前缀和后缀都为空集，共有元素的长度为0
2. “AB”的前缀为A，后缀为B，共有元素为0
3. “ABC”的前缀为A，AB后缀为BC，C共有元素的长度为0
4. “ABCDA”的前缀为A，AB,ABC,ABCD，后缀为BCDA,CDA,DA,A共有元素为A，长度为1

我们可以这样理解，对于一个字符的匹配值判断，就看他和前面的第几个字符相等

比如ABCDABD，ABCD的匹配值均为0，但是A与前缀ABCD中的A相同，故匹配值为1，AB与前缀ABCD中的AB相同，故B的匹配值为2，ABD没有与之相同的前缀，故D为0

代码

    //生成匹配值next数组
    private static int[] ArrayNext(char[] s2) {
        int[] next = new int[s2.length];
        next[0]=0;//如果字符串长度为1，部分匹配值就是0
        for (int i=1,j=0;i<s2.length;i++){
            if(j>0&&s2[i]!=s2[j]){
                j=j-1;
            }
            if(s2[i]==s2[j]){
                j++;
            }
            next[i]=j;
        }
        return next;
    }

    private static int check(char[] s1, char[] s2) {
        int[] next = ArrayNext(s2);
        int t=0;
        int b=0;
        while (t<s1.length){
            if(s1[t]!=s2[b]){
                t++;
            }else {
                //第一个字符匹配上了
                while (b!=s2.length-1){
                    t++;
                    b++;
                    if(s1[t]!=s2[b]){
                        t=t-b+(b-next[b-1]);
                        b=0;//10-6+7-2
                        break;
                    }
                }
                if (b==s2.length-1){
                    return t-b;
                }
            }
        }
        return -1;
    }