机器学习回归算法-精讲
Posted ZSYL
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习回归算法-精讲相关的知识,希望对你有一定的参考价值。
回归算法
回归算法
数据类型分为连续型和离散型。离散型的数据经常用来表示分类,连续型的数据经常用来表示不确定的值。比如一个产品质量分为1类,2类,这是离散型。房价1.4万/平,3.4万/平,这是连续型。之前我们学的都是分类,那么对于一些连续型的数据,我们就可以通过回归算法来进行预测了。
回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。那么什么是线性关系和非线性关系?
线性回归和非线性回归:
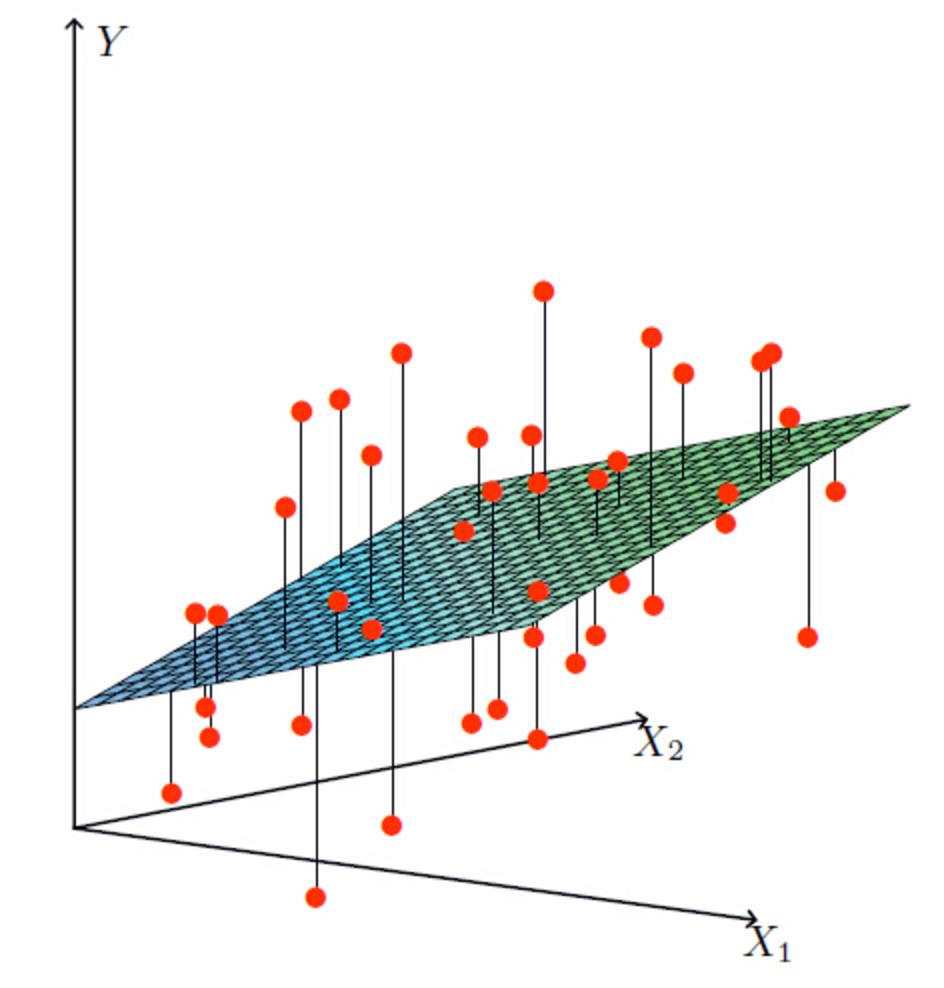
比如说在房价上,房子的面积和房子的价格有着明显的关系。那么X=房间大小,Y=房价,那么在坐标系中可以看到这些点:
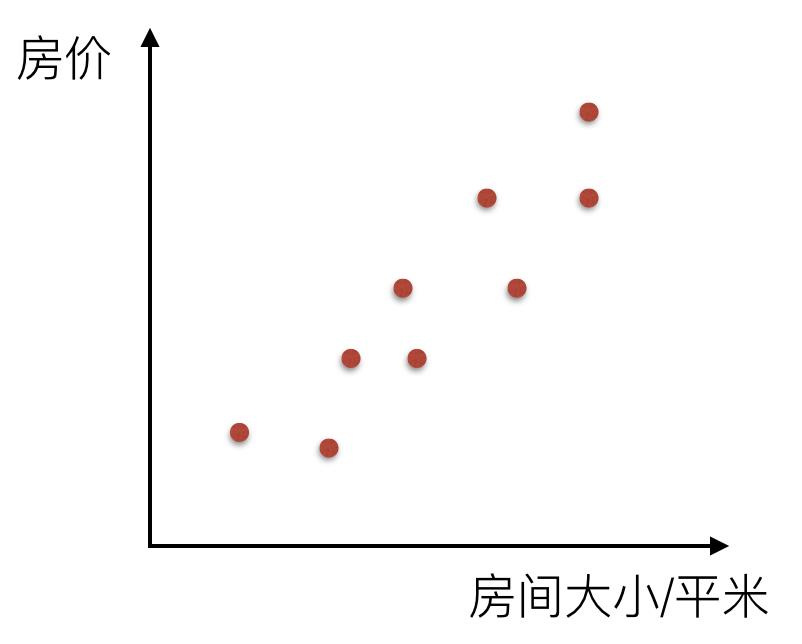
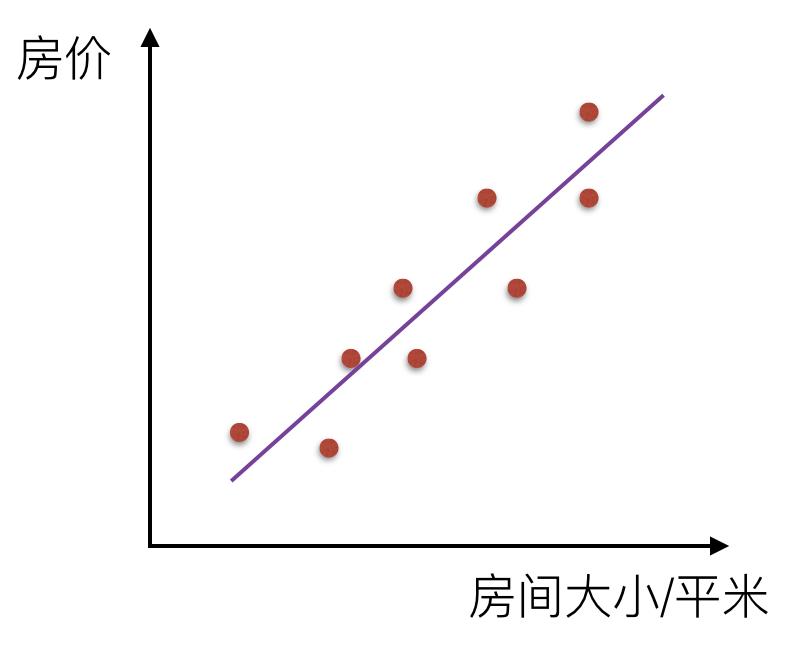
如果房间面积大小和房价的关系可以用一根直线表示,那么这就是线性关系:
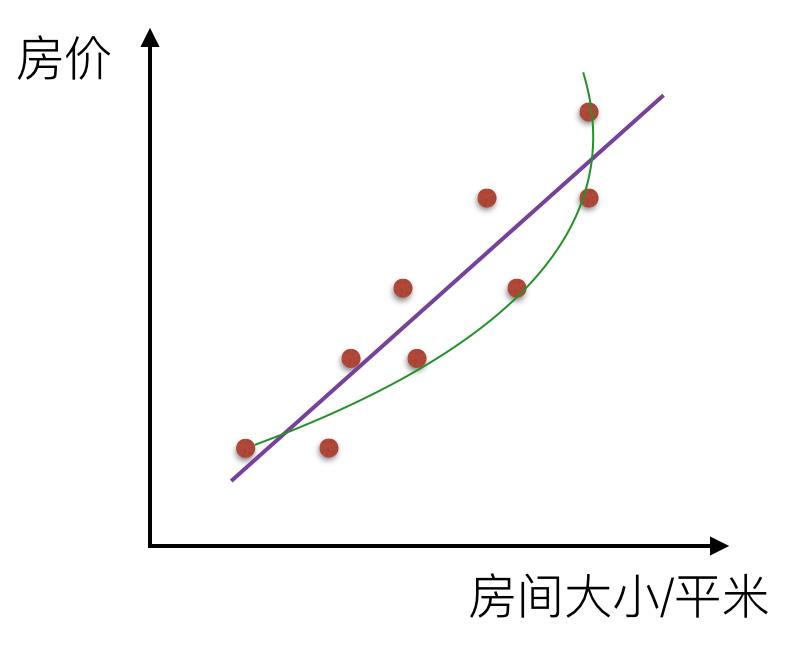
而如果不是一根直线,那么就是非线性关系:
线性回归
线性回归通过一个或者多个自变量与因变量之间进行建模的回归分析。其中特点为一个或多个称为回归系数的模型参数的线性组合。
线性回归方程:
线性回归方程,就是有k个特征,然后每个特征都有相应的系数,并且在所有特征值为0的情况下,目标值有一个默认值。因此线性回归方程如下:
h
(
𝑤
)
=
𝑤
₀
+
𝑤
₁
∗
𝑥
₁
+
𝑤
₂
∗
𝑥
₂
+
…
ℎ(𝑤)= 𝑤₀ + 𝑤₁*𝑥₁ + 𝑤₂*𝑥₂+…
h(w)=w₀+w₁∗x₁+w₂∗x₂+…
整合后的公式为:
h
(
w
)
=
∑
i
n
w
i
x
i
=
θ
T
x
h(w)=∑_i^nw_ixi=θ^Tx
h(w)=i∑nwixi=θTx
损失函数:
损失函数是一个贯穿整个机器学习重要的一个概念,大部分机器学习算法都会有误差,我们得通过显性的公式来描述这个误差,并且将这个误差优化到最小值。
假设现在真实的值为y,预测的值为h,那么损失函数的公式如下:
J
(
θ
)
=
1
2
∑
i
m
(
y
(
i
)
−
θ
T
x
(
i
)
)
2
J(θ)=\\frac{1}{2}∑_i^m(y^{(i)}-θ^Tx^{(i)})^2
J(θ)=21i∑m(y(i)−θTx(i))2
也就是所有误差和的平方。损失函数值越小,说明误差越小.这个损失函数也有一个专门的叫法,叫做最小二乘法。
损失函数推理过程:
公式转换:
首先,我们是想要获取到这样一个公式:
h
(
θ
)
=
θ
0
+
θ
1
∗
x
1
+
θ
2
∗
x
2
+
…
ℎ(θ)= θ_0 + θ_1*x_1 + θ_2*x_2+…
h(θ)=θ0+θ1∗x1+θ2∗x2+…
那么为了更好的计算,我们将这个公式进行一些变形,将
w
0
w_0
w0后面加个
x
0
x_0
x0,只不过这个
x
0
x_0
x0是为1。所以可以变化成以下:
h
(
θ
)
=
∑
i
n
θ
i
x
i
ℎ(θ)= ∑_i^nθ_ix_i
h(θ)=i∑nθixi
而
θ
i
θ_i
θi和
x
i
x_i
xi可以写成一个矩阵:
[
θ
0
θ
1
θ
3
.
.
.
]
\\left[\\begin{matrix} θ_0 θ_1 θ_3 ... \\end{matrix} \\right]
[θ0θ1θ3...] x
[
1
x
1
x
3
.
.
.
]
\\left[\\begin{matrix} 1 \\\\ x_1 \\\\ x_3 \\\\ ... \\end{matrix} \\right]
⎣⎢⎢⎡1x1x3...⎦⎥⎥⎤ =
∑
i
n
θ
i
x
i
∑_i^nθ_ix_i
∑inθixi =
θ
T
x
θ^Tx
θTx
用矩阵主要是方便计算。
误差公式:
其次,以上求得的,只是一个预测的值,而不是真实的值,他们中间肯定会存在误差,因此会有以下公式:
y
i
=
θ
i
x
i
+
ϵ
i
y_i=θ_ix_i + ϵ_i
yi=θixi+ϵi
我们要做的,就是找出最小的
ϵ
i
ϵ_i
ϵi,使得预测值和真实值的差距最小。
转化为θ求解:
然后,
ϵ
i
ϵ_i
ϵi是存在正数,也存在负数,所以可以简单的把这个数据集,看做是一个服从均值为0,方差为
σ
2
σ^2
σ2的正态分布。所以
ϵ
i
ϵ_i
ϵi出现的概率为:
p ( ϵ i ) = 1 2 π σ e x p − ( ϵ i ) 2 2 σ 2 p(ϵ_i)=\\frac{1}{\\sqrt{2π}σ}exp{\\frac{-(ϵ_i)^2}{2σ^2}} p(ϵi)=2πσ1exp2σ2−(ϵi)2
把 ϵ i = y i − θ i x i ϵ_i=y_i-θ_ix_i ϵi=yi−θixi代入到以上高斯分布的函数中,变成以下式子:
p
(
ϵ
i
)
=
1
2
π
σ
e
x
p
−
(
y
i
−
θ
i
x
i
)
2
2
σ
2
以上是关于机器学习回归算法-精讲的主要内容,如果未能解决你的问题,请参考以下文章 深度学习核心技术精讲100篇(八十二)-Statsmodels线性回归看特征间关系