因果推断笔记——双重差分理论假设实践

Posted 2021-12-11 悟乙己

文章目录

• 1 双重差分 - difference-in-difference -DID 理论与假设
• • 1.1 DID介绍
  • 1.2 使用时需要满足的假设
• 2 DID + PSM 差异与联用
• • 2.1 DID / PSM差异
  • 2.2 解决平行趋势假设：DID+PSM连用（最常用）
• 3 三重差分（Difference-in-differences-in-differences, DDD）
• 3 相关实现案例
• • 3.1 快手使用DID模型
  • 3.2 淘系用户增长注意点

---

1 双重差分 - difference-in-difference -DID 理论与假设

1.1 DID介绍

本节参考：
因果推断综述及基础方法介绍（一）
双重差分法（DID）的原理与实际应用

【3.0章节】 中随机实验有提到，ATE = E(Yi|Ti=1)−E(Yi|Ti=0)的前提是T⊥(Y(1),Y(0))，
也就是干预与Y是独立的、无因果、非内生
那如果不符合这个条件应该怎么办？
有一个比较老且基础的方法是双重差分法，也就是差分两次。

另外的特点：

• 在一定程度上减轻了选择偏差和外因带来的影响；
• 不同于往常基于时序数据的分析，双重差分利用的是面板数据。

或者：

这张图讲得非常清楚，首先为什么我们不能用ATE = E(Yi|Ti=1)−E(Yi|Ti=0)，举个 ，我们给一些人发权益，另一些人不发，我们怎么能知道权益带来的购买效果是怎么样的呢？简单的方法就是给发权益的人购买数加和，不发权益的人购买数加和，然后两个加和相减就好啦，但是如果这两部分人本来不发权益的时候购买数就不一样呢？

那就减两次，从上图来说：

• **第一次差分：**我们把这两群人发权益之前t0的购买数相减，得到一个差值，相当于这两群人的固有差距
• **第二次差分：**再把这两群人发权益之后t1的购买数相减，相当于这两群人被权益影响之后的差距

后面的差距减去前面的差距，就会得到权益对于差距有多少提升（降低），以此作为权益的effect。

这个方法的问题在于有个比较强的假定是，趋势平行，也就是要求t0到t1之间，两群人的购买概率变化趋势是一样的（图中那个平行线），这其实是一个很强的假设，所以这个方法我个人来讲不算非常认可。

1.2 使用时需要满足的假设

双重差分法的计算过程很简单，即实验组干预前后的均值的差减去对照组干预前后均值的差。
但若希望得到的结果是准确的，对应的样本数据需要满足下面三个假设：

• 线性关系假设：该假设来自于线性回归，认为因变量（Treatment）与结果变量存在线性关系
• 个体处理稳定性假设（The Stable Unit Treatment Value Assumption，SUTVA）
  个体的outcome是取决于个体干预变量treatment的一个函数，该假设由两部分组成
  • 一致性（Consistency）：个体接受处理后所导致的潜在结果是唯一的。
    例：我养狗了会变开心，无论是什么狗、不存在因为狗是黑的就不开心
  • 互不干预（No interference）：个体接受处理后导致的潜在结果不受其他个体处理的影
    例：我在淘宝上领到了红包之后会更愿意买东西，不因为我同事也领了红包就意愿降低了
• 平行趋势假设（Parallel Trend Assumption）
  定义：实验组和对照组在没有干预的情况下，结果的趋势是一样的。即在不干预的情况下，前后两个时间点实验组与对照组的差值一致。

2 DID + PSM 差异与联用

2.1 DID / PSM差异

DID, PSM 及 DID+PSM 有何差异？DID 要假定不可观测效应随时间变化趋势相同？

• DID: difference in difference, 双重差分；
• PSM: propensity score matching, 倾向评分匹配；
• DID(PS)M: difference in difference (propensity score) matching, 双重差分（倾向评分）匹配

一个比较简单的差异对比版本：

• DID是比较四个点，Treated before, treated after; control before, control after。
• Matching是比较两个点：Treated, control
• DID＋Matching是用matching的方法来确定treated和control。

适用范围：

• DID： 适合面板数据，从全部效应中剔除“时间趋势”（姑且勉强称之为时间趋势，即未经政策影响的自然变化，其影响因素是不可观测的，或者说不能穷尽）的影响，此时我们需要一个控制组去衡量这一“时间趋势”，数据前提要求为面板数据。
• PSM： PSM更加适用于截面数据，或者将面板数据作为截面数据来处理；PSM实际上寻找与处理组尽可能相似的控制组样本，当协变量维度比较多的时候，借助probit或logit模型（分组虚拟变量对协变量进行回归），将多维的协变量信息通过倾向得分（概率拟合值，scalar）来刻画。
• PSM+DID： DID的一个最重要的前提是平行趋势假设，如果不满足，控制组就不能作为实验组的反事实结果。此时，可以借助PSM的方法，构造一个与实验组满足平行趋势的控制组，接下来按照DID的方法去做就可以了。此时，有同学可能会问，PSM已经构造了一个控制组样本组合，为什么还要多此一举，再加一个DID上去。
  PSM需要控制尽可能多的控制变量，以使分组变量完全随机，而对于有一些变量，一方面不可观测，另一方面又不随时间而改变，此时就可以使用PSM+DID的方法。

2.2 解决平行趋势假设：DID+PSM连用（最常用）

双重差分法（DID）的原理与实际应用

具体PSM的实现过程可见：因果推断笔记——python 倾向性匹配PSM实现示例（三）

• 目的：从干预的人群和未干预的人群里找到两批人符合平行趋势假设
• 业务理解：在这两个人群里找个两批同质的人（该场景下的同质：在treatment维度上有近似表现的- 人）
• 例子：在探究领取红包对用户购买行为影响的场景下，对用户领取红包的倾向做预测（打分），认为分数相近的用户是matching、即同质的。圈选出分数相同的用户之后再验证平行趋势假设。

完成PSM后数据会呈现一些规律（如图所示）：

• 干预人群与非干预人群的score分布 —— 匹配后分布一致
• 抽样后人群在一些画像（如年龄、性别、职业）上的分布会更接近

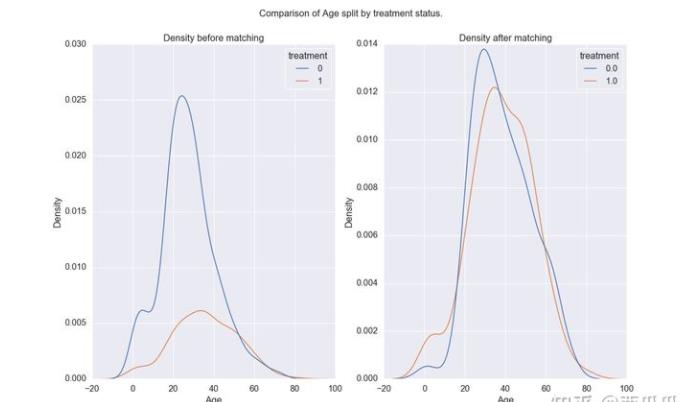
这里后台的操作步骤是，为treatment1 找到哪些比较贴近的样本：

• 数据量本身就会减少，只筛选与T=1 相似的那部分样本

那么这里的PSM起到了一个，筛选指定样本的功能。同理在一些比赛中，也可以使用，作为训练集 / 测试集分布鉴定的方式。

3 三重差分（Difference-in-differences-in-differences, DDD）

双重差分法（DID）的原理与实际应用

定义：再做一次双重差分消除实验与对照组差异带来的增量，剩下的即干预带来的增量。

三重差分的概念比较抽象，这里通过一个例子来说明：

• 背景：假设淘宝针对杭州的学生（实验组）发放红包，其他人不发。如果想衡量红包带来的转化增量，直观的会选用杭州的非学生作为对照组。但由于学生和非学生的购买力和趋势本身具有差异，此时平行趋势假设无法满足。
• 解决方案：此时我们可以引入一个其他的城市，譬如宁波。计算宁波学生与非学生的DID，可以认为这里的DID是来自于人群差异的增量；最后我们用杭州的DID减去宁波的DID则得到发红包带来的净效应。

注 ：使用三重差分法时，红线与绿线、紫线与橙线间仍需满足平行趋势假设。（这也是DDD不常用的原因）

3 相关实现案例

3.1 快手使用DID模型

同一对象的同一干预treatment，前、后两个时间段的差异,

关键假设是，政策干扰前存在平行趋势，且实验干扰效应不随时间变化。
双重差分可以用来消除那些对后期可能存在干扰因素，得到实验效果估计。

快手的升级方案：分不同类型进行分项评估
用户的行为会发生变化，且不同用户的行为是不一致的，当不同表现用户都在实验组，传统的DID模型估计实验效应会产生偏差。
按照用户的状态是否更改分为不同类型，对不同类型用户分别做DID估计，再进行加权平均，得到修正后DID实验效果值。

3.2 淘系用户增长注意点

双重差分法（DID）的原理与实际应用
当随机分流的量级不一致时，也可能会导致不同质，因为量级越大存在多个user_id对应一个自然人的情况越多，会影响user_id粒度的指标统计；
对于一般的AB分流，我们可以通过分流后两组人群在性别、年龄等属性上分布的相似度来检验同质性。