(王道408考研数据结构)第三章栈和队列-第一节:栈基本概念顺序栈和链栈基本操作
Posted 我擦了DJ
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了(王道408考研数据结构)第三章栈和队列-第一节:栈基本概念顺序栈和链栈基本操作相关的知识,希望对你有一定的参考价值。
文章目录
一:栈基本概念
(1)栈的定义
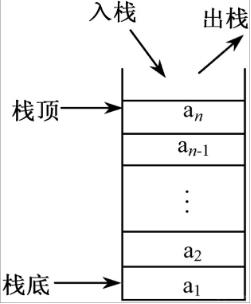
栈(stack):是一种将插入和删除操作限制在一端进行的线性表。我们把允许插入和删除的一端称之为栈顶(top),另一端则称之为栈顶(bottom),不含任何数据元素的栈称之为空栈。栈中元素遵循后进先出原则
-
类似于生活中的弹夹中的子弹,先压进去的子弹是最后出来的
-
一些软件(例如Word,Photoshop)其撤销操作其实本质也是栈结构
(2)压栈和出栈
压栈:是栈的插入操作,也叫做进栈、入栈
出栈:是栈的删除操作,也叫做弹栈
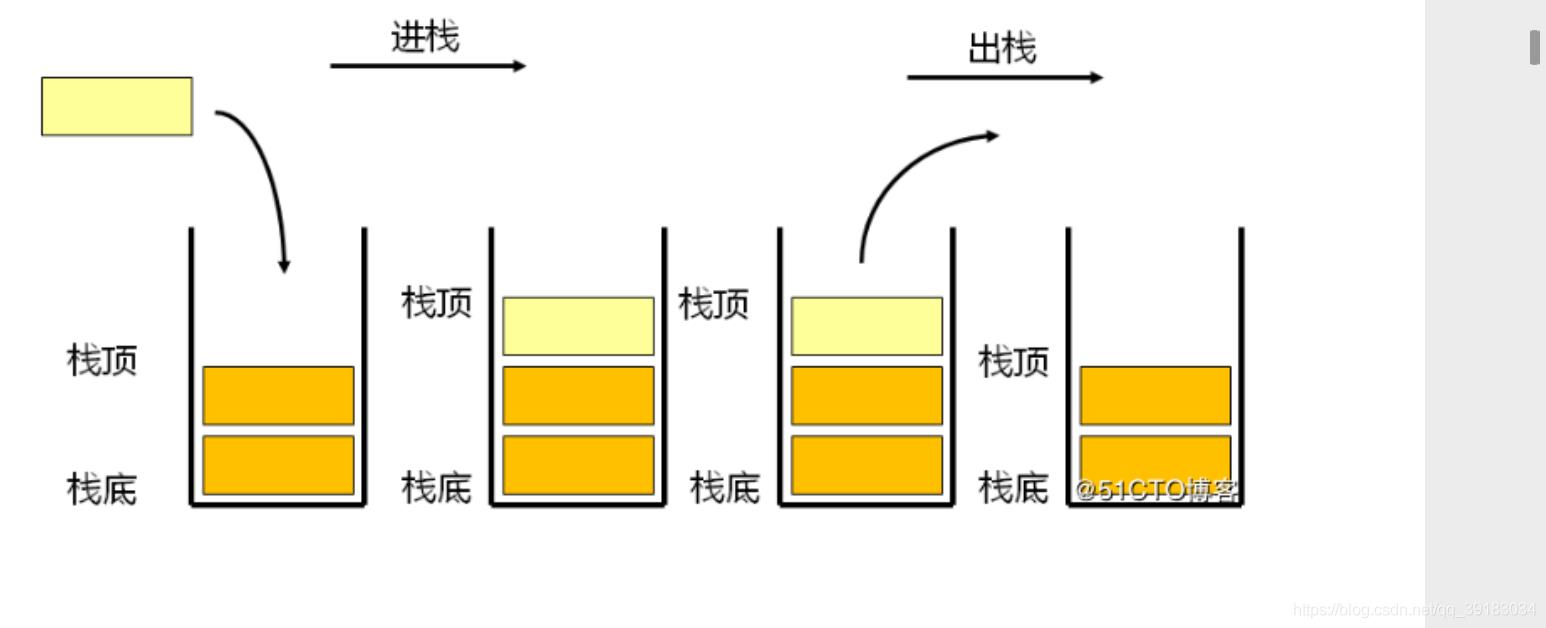
如下
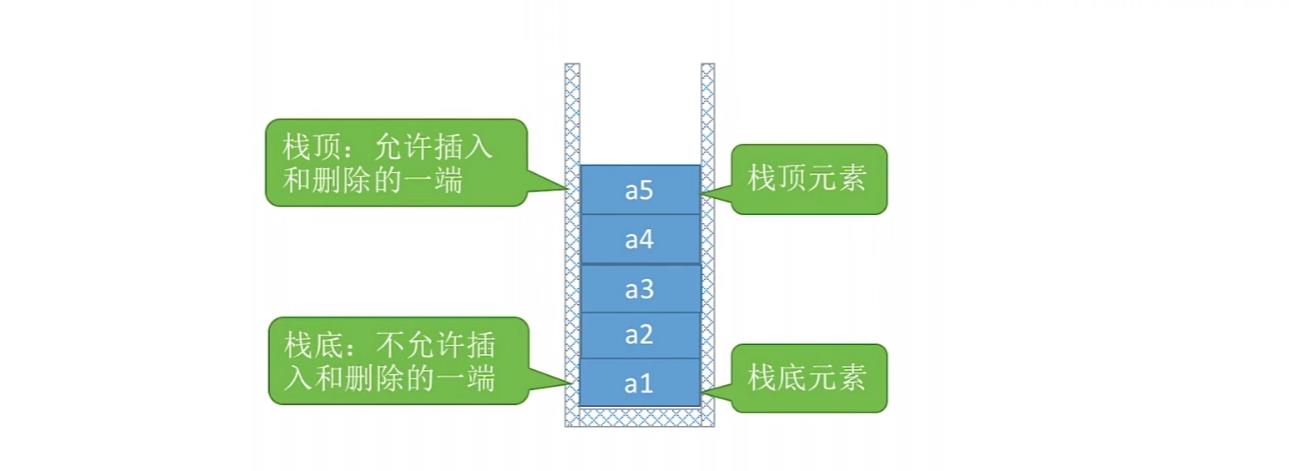
- 进栈顺序: a 1 a_{1} a1-> a 2 a_{2} a2-> a 3 a_{3} a3-> a 4 a_{4} a4-> a 5 a_{5} a5
- 出栈顺序: a 5 a_{5} a5-> a 4 a_{4} a4-> a 3 a_{3} a3-> a 2 a_{2} a2-> a 1 a_{1} a1
(3)进栈出栈变化形式
值得注意的是,栈对线性表的插入和删除是在位置上进行了限制,但是并没有对进出时机进行限制,也就说,在不是所有元素都进栈的情况下,事先进去的元素也可以出栈,只要保证位置是栈顶即可
比如现在有3个整型数字元素 1 1 1、 2 2 2、 3 3 3依次进栈,会有哪些出栈次序呢?
- 第一种: 1 1 1、 2 2 2、 3 3 3进,然后再 3 3 3、 2 2 2、 1 1 1。出栈次序为 3 3 3 2 2 2 1 1 1
- 第二种: 1 1 1进、 1 1 1出; 2 2 2进、 2 2 2出; 3 3 3进、 3 3 3出。出栈次序为 123 123 123
- 第三种: 1 1 1进、 2 2 2进、 2 2 2出、 1 1 1出、 3 3 3进、 3 3 3出。出栈次序为 213 213 213
- 第四种: 1 1 1进、 1 1 1出、 2 2 2进、 3 3 3进、 3 3 3出、 2 2 2出。出栈次序为 132 132 132
- 第五种: 1 1 1进、 2 2 2进、 2 2 2出、 3 3 3进、 3 3 3出、 1 1 1出。出栈次序为 231 231 231
但是像 312 312 312这种情况是绝对不可能出现的。因为 3 3 3先出栈,就意味着 3 3 3曾经进栈,既然 3 3 3都进栈了,那么也就意味着 1 1 1和 2 2 2已经进栈了,此时 2 2 2一定是在 1 1 1的上面,出栈只能是 321 321 321
其实,
n
n
n个不同元素进栈,出栈元素不同排列的个数可由卡特兰(
C
a
t
a
l
a
n
Catalan
Catalan)数确定:
N
=
1
n
+
1
C
2
n
n
N=\\frac{1}{n+1}C^{n}_{2n}
N=n+11C2nn
- 比如上面的3个元素就有 1 3 + 1 C 6 3 = 1 4 × 6 × 5 × 4 3 × 2 × 1 = 5 \\frac{1}{3+1}C_{6}^{3}=\\frac{1}{4}×\\frac{6×5×4}{3×2×1}=5 3+11C63=41×3×2×16×5×4=5种
- 卡特兰数证明有兴趣可以移步点击跳转
(4)栈的操作
一个栈的基本操作如下
InitList(&L):初始化表DestoryList(&L):销毁草案做ListInsert(&L,i,e):插入操作ListDelete(&L,i,&e):删除操作LocateElem(L,e):按值查找GetElem(L,i):按位查找
其它常用操作
Length(L):求表长PrintList(L):输出操作Empty(L):判空操作
二:栈的顺序存储结构及其操作实现
(1)顺序栈的定义
顺序栈:顺序栈自然而然使用数组来实现。采用下标为0的一端作为栈顶,这样的话数组尾部作为栈顶以进行插入和删除
由于尾部元素作为栈顶,也就是最后一个元素是栈顶元素,所以需要使用一个 变量top 进行标识,top之外元素将不属于栈的定义范围,通常把top=-1定义为空栈
- 这有点像游标卡尺的游标,游标(
top)可以随意变大或变小,但是不能超出尺子的范围

因此顺序栈结构定义如下
#define MaxSize 10
typedef struct
{
DataType arr[MaxSize];
int top;//栈顶指针
}SqStack;
假定MaxSize=5,顺序栈栈常见的情况如下
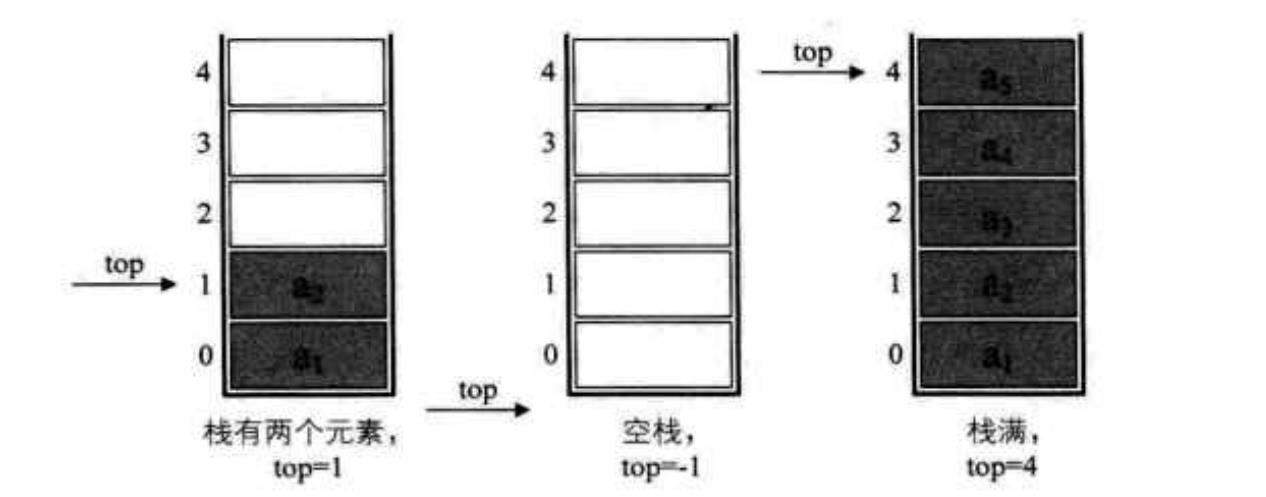
- 所以栈空的充要条件为
top==-1
(2)进栈
进栈:进栈时,先栈顶指针+1,后进行元素赋值(若top初值为0逻辑恰好相反)

代码如下,注意栈满判断
bool Push(SqStack& S,Datatype e)
{
if(S.top==MaxSize-1)
return false;//栈满
S.top+=1;
S.data[S.top]=e;
return true;
}
(3)出栈
出栈:处栈时,先保存元素,后栈顶指针-1(若top初值为0逻辑恰好相反)
- 注意这种删除只是逻辑上的删除,其元素仍然留在那片区域里。因为我们研究的是栈,只研究的是
0~top这个范围内的情况
代码如下,注意栈空判断
bool Pop(SqStack& S,DataType& e)
{
if(S.top==-1)
return false;//栈空
e=S.data[S.top];
S.top-=1;
return true;
}
(4)读取栈顶元素
代码如下
bool GetTop(SqStack& S,DataType& e)
{
if(S.top==-1)
return false;//栈空
e=S.data[S.top];
return true;
}
(5)共享栈
顺序栈其缺点就在于事先要确定空间大小,万一不够用需要进行扩容,很是麻烦。另一种解决方法就是利用共享栈
共享栈:有两个相同类型的栈,如果一个栈空间满了,就可以借助另一个栈的空间。具体来说,可以让一个栈的栈底为“栈”始端,即数组下标0处,另一个栈为“栈”末端,即数组下标n-1处,增加元素时,就是两端点向中间延伸
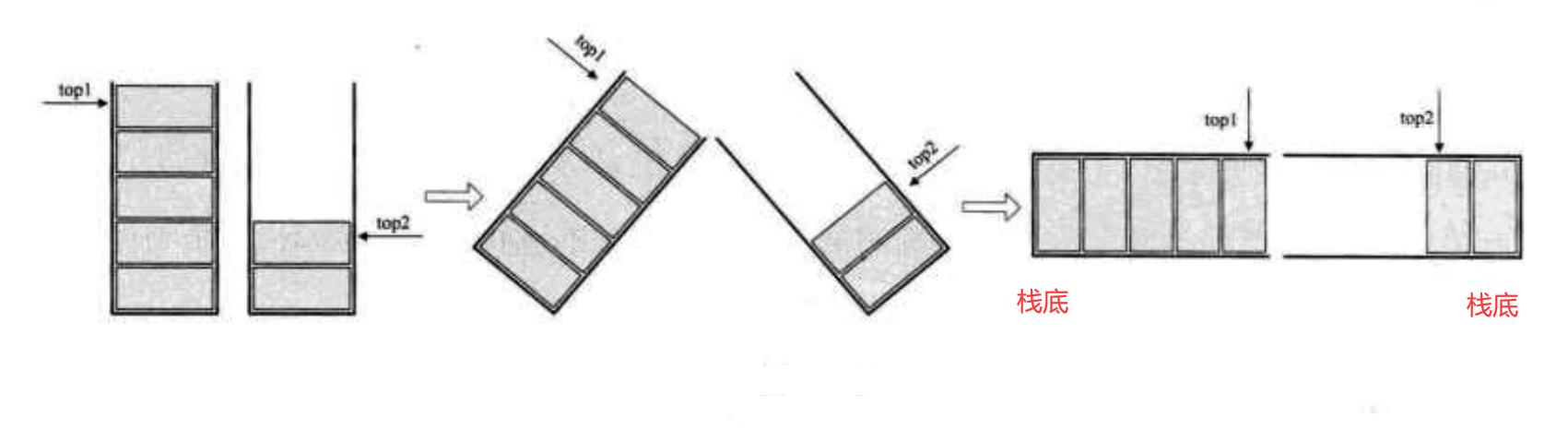
不难想象,其判空和判满条件如下
判空:top1==-1且top2==n
判满:普通情况下,top1和top2一般不碰面。但是当top1+1==top2时肯定就满了
共享栈结构定义如下
typedef struct
{
DataType arr[MaxSize];
int top1;//栈1的栈顶指针
int top2;//栈2的栈顶指针
}SqDoubleStack;
共享栈压栈代码如下,注意需要一个变量StackNumber用于标识是哪个栈进栈
bool Push(SqDoubleStack& S,DataType e,int StackNumber)
{
if(S.top1+1==S.top2)
return false;
if(StackNumber==1)//栈1进栈
S.data[++s.top1]=e;
if(StackNumber==2)//栈1进栈
S.data[--s.top2]=e;
return true;
}
共享栈出栈代码如下
bool Pop(SqDoubleStack& S,DataType& e,int StackNumber)
{
if(StackNumber==1)
{
if(S.top1==-1)//栈1已经是空栈
return false;
e=S.data[S.top1--];
}
else if(StackNumber==2)
{
if(S.top2==MaxSize)//栈2是空栈
return false
e=S.data[S.top2++];
}
return true;
}
三:栈的链式存储结构及其操作实现
(1)链栈的定义
链栈:这是栈的链式存储结构。对于单链表来说它本身就具有头指针,所以可以让头指针和栈顶指针合二为一。同时,栈顶元素就在头部,因此头结点失去意义,所以对于链栈来说是不需要头结点的
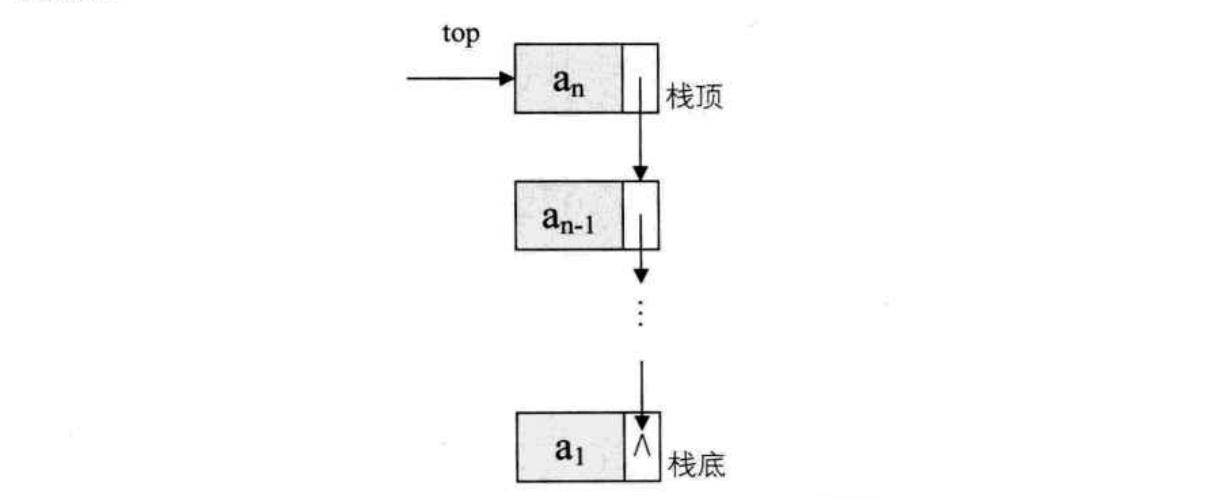
因此链栈结构定义如下
typedef struct StackNode//结点定义
{
DataType data;
struct StackNode* next;//指向下一个结点
}StackNode;
typedef stuct LinkStack
{
StckNode* top;//栈顶指针
int count;//栈结点数目
}LinkStack;
(2)进栈
进栈:链栈进栈相当于单链表的插入操作
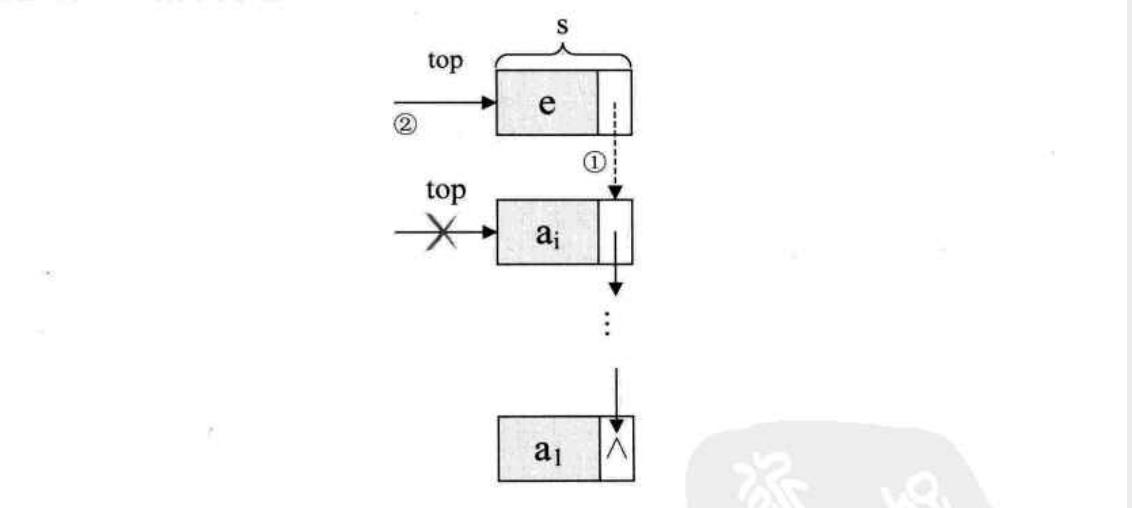
代码如下,无序考虑栈满情况
bool Push(LinkStack& S,DataType e)
{
StackNode NewNode(StackNode*)malloc(sizeof(StackNode));//申请一个栈结点
NewNode.data=e;
NewNode.next=S.top;//此时NewNode即将作为栈顶结点,那么它的下面的元素就是之前的栈顶结点
S.top=NewNode;
S.count++;
return true;
}
(3)出栈
出栈:链栈进栈相当于单链表的删除操作
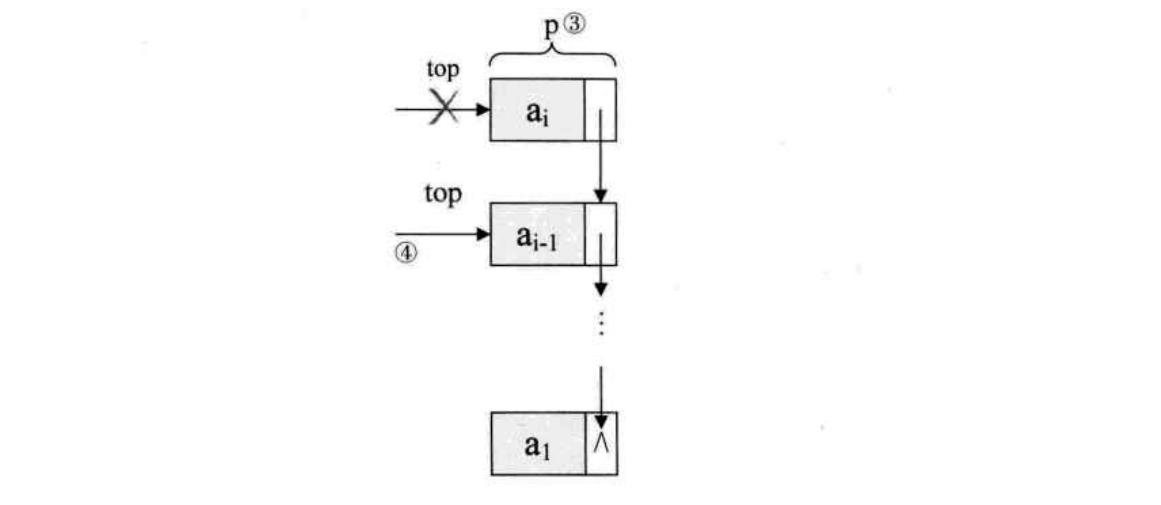
代码如下,需要考虑栈空情况
```c
bool Pop(LinkStack& S,DataType& e)
{
StackNode p;//临时结点,便于销毁删除结点
if(StackEmpty(S))
return false;
e=S.top->data;
p=S.top;
S.top=S.top->next;//栈顶指针后移
free(p);//释放删除结点空间
S.count--;
return true;
}
以上是关于(王道408考研数据结构)第三章栈和队列-第一节:栈基本概念顺序栈和链栈基本操作的主要内容,如果未能解决你的问题,请参考以下文章
(王道408考研数据结构)第三章栈和队列-第二节:队列基本概念顺序栈和链栈基本操作
(王道408考研操作系统)第三章内存管理-第一节7:非连续分配管理方式之基本分段管理方式
(王道408考研操作系统)第三章内存管理-第一节7:非连续分配管理方式之基本分段管理方式
(王道408考研数据结构)第三章栈和队列-第三节2:栈的应用之递归