(王道408考研数据结构)第三章栈和队列-第三节1:栈的应用之括号匹配问题和表达式问题(前缀中缀和后缀)
Posted 我擦了DJ
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了(王道408考研数据结构)第三章栈和队列-第三节1:栈的应用之括号匹配问题和表达式问题(前缀中缀和后缀)相关的知识,希望对你有一定的参考价值。
前面我们就说过,栈一种后进先出的线性表,这种后进先出的特性就决定了它在一类场合或问题中会经常被用到——递归。考研数据结构中所涉及的利用栈结构解决递归问题或者考察栈结构特性的问题主要有这么几类
- 括号匹配问题
- 表达式转换、计算问题
- 递归问题(篇幅限制,点击跳转-(王道408考研数据结构)第三章栈和队列-第三节2:栈的应用之递归)
一:括号匹配问题
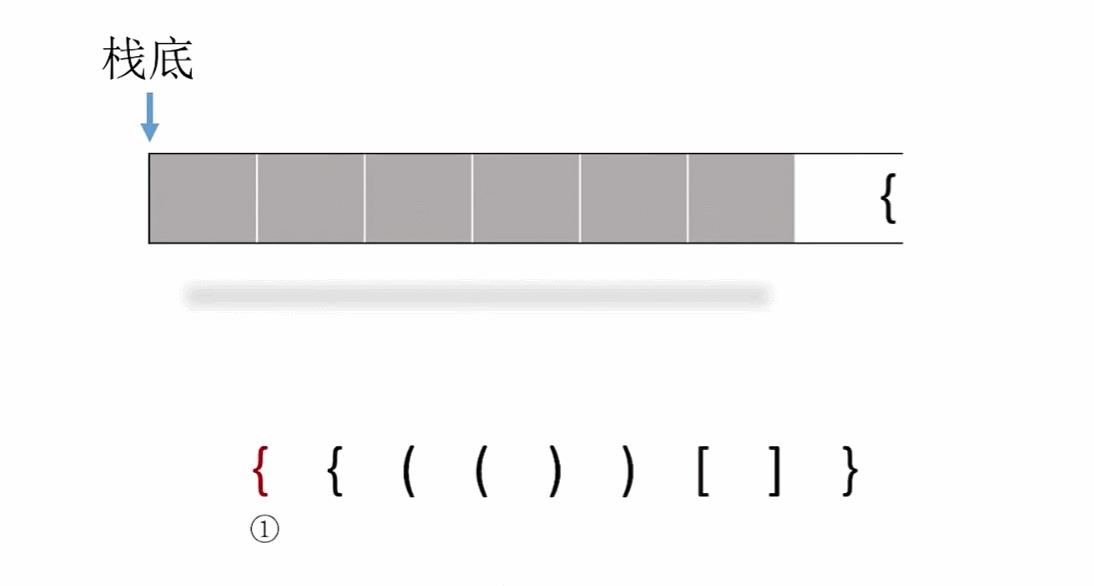
括号匹配问题是指给出你一个随机的括号序列,例如([{}]),让你判断该序列是否匹配。这种问题思路也是非常简单,也是很直接的利用到了栈结构的特性
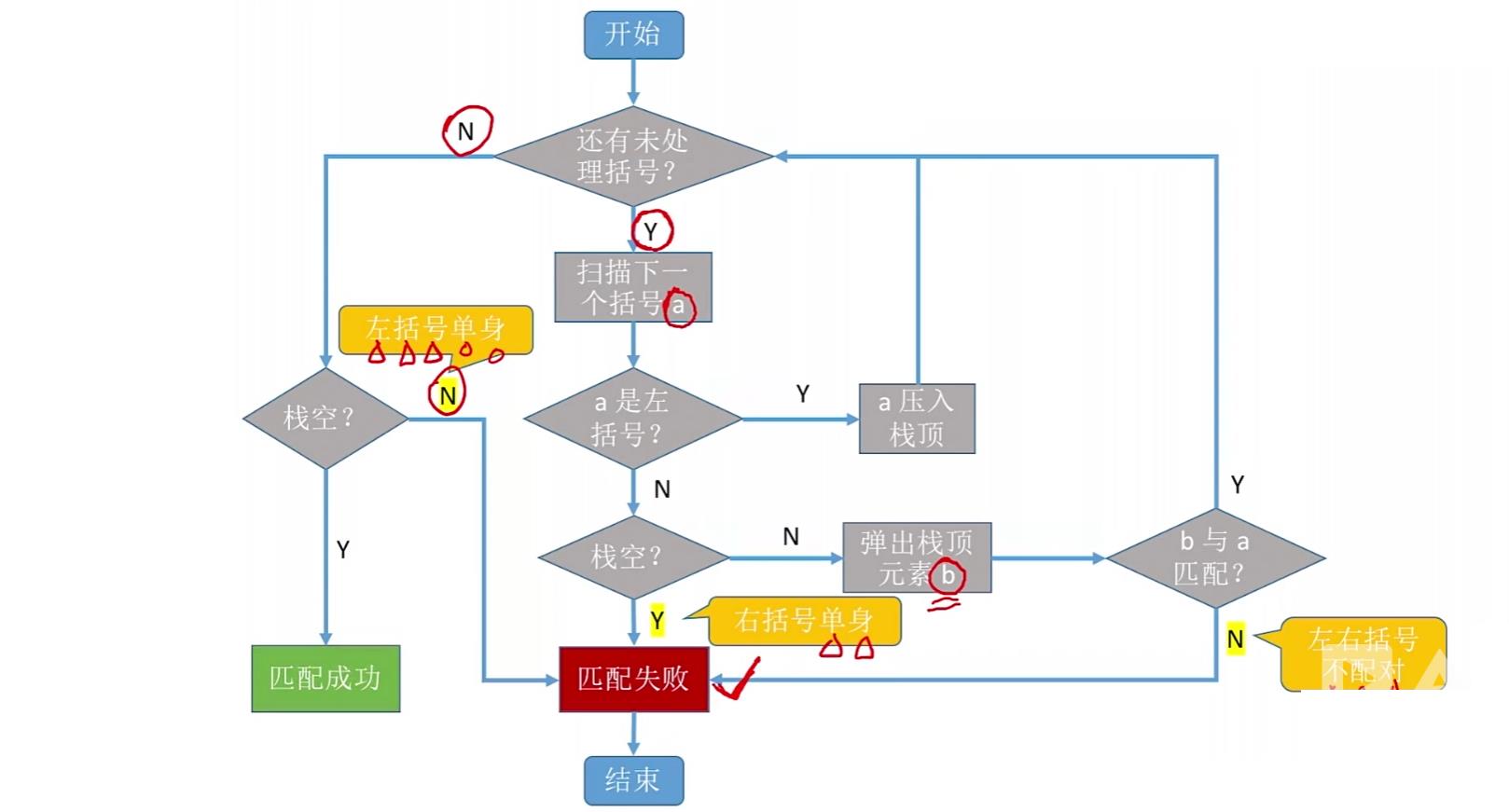
算法思想:从左向右依次扫描给定序列,如果遇到左括号就进栈;如果遇到右括号需要进行以下判断:
- 栈空:匹配失败,说明没有与之对应的左括号
- 栈不空,取栈顶元素不匹配:匹配失败,说明左右括号不配对
- 栈不空,取栈顶元素匹配:这一对匹配成功,继续进行下一对
另外如果扫描到最后栈中还有元素,这说明没有与之对应的右括号,匹配失败
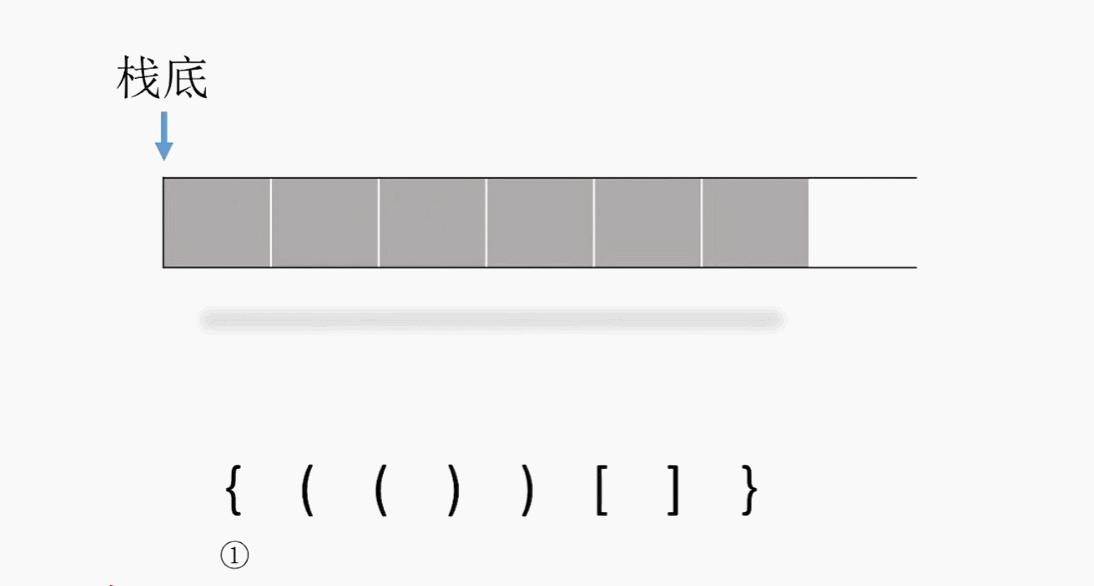
示例
匹配成功
左右不匹配
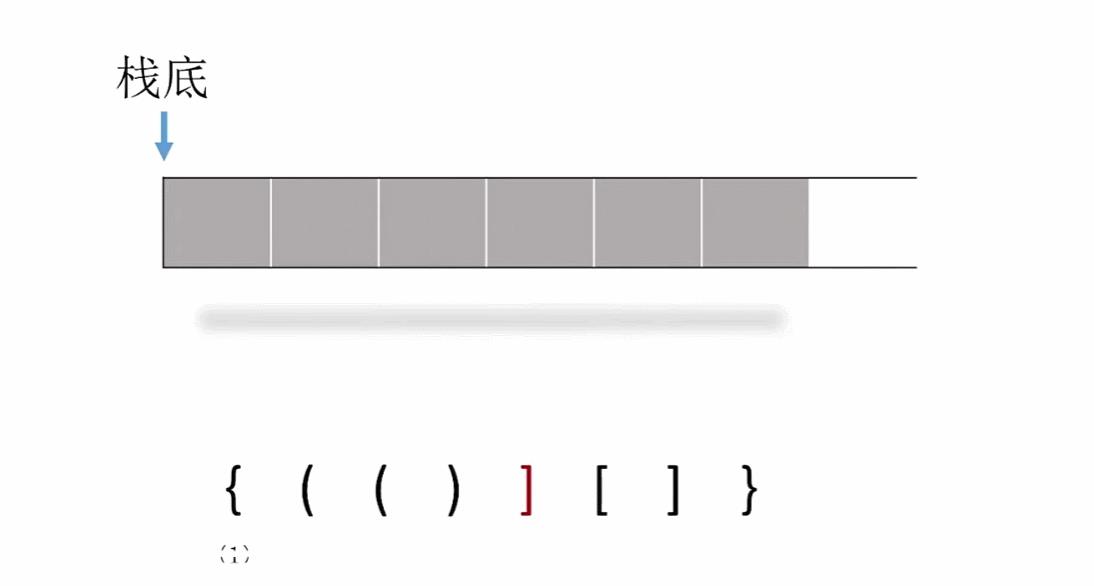
没有对应的左括号
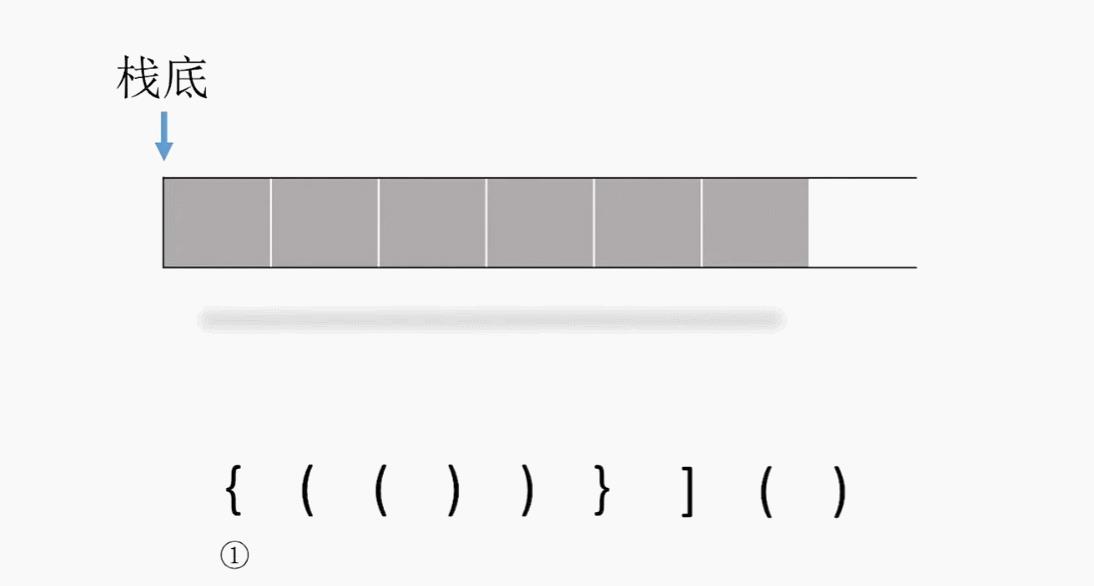
没有对应的右括号
代码
#define MaxSize 10
typedef struct
{
char data[MaxSize];
int top;
}SqStack
void InitStack(SqStack& S);//初始化
void StackEmpty(SqStack S);//判空
void Push(SqStack& S,char x);//入栈
void Pop(SqStack& S,char& x);//出栈
bool Check(char str[],int len)
{
SqStack S;
InitStack();
for(int i=0;i<len;i++)
{
if(str[i]=='(' || str[i]=='[' || str[i]=='{')//扫描到左括号入栈
Push(S,str[i]);
else//扫描到右括号
{
if(StackEmpty(S))//没有与之对应的左括号
return false;
char top;
Pop(S,top);//拿出栈顶元素判断
if(//这三种都属于左右括号不匹配情形
(str[i]==')' && top!='(') ||
(str[i]==']' && top!='[')||
(str[i]=='}' && top!='{')
)
return false;
}
}
//扫描完成,且栈空了,表明匹配成功
return StackEmpty(S);
}
二:表达式问题
中缀表达式:a+b
前缀表达式(波兰式):+ab
后缀表达式(逆波兰式):ab+
(1)表达式转换

- 只要能掌握中缀转前缀,前缀转中缀,中缀转后缀和后缀转中缀即可
A:手工转换
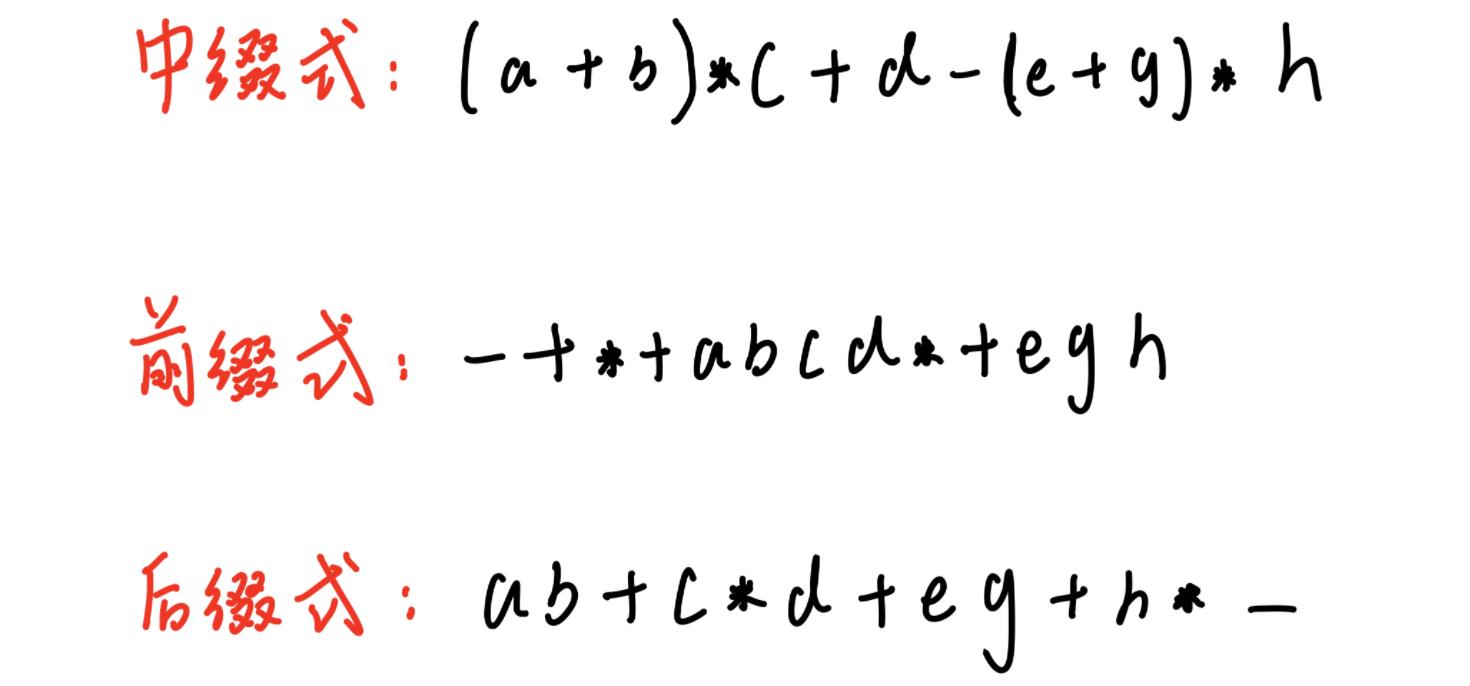
①:中缀转前缀和中缀转后缀
原则:每遇到两个操作数,一个运算符就把他们用括号扣起来(括号部分可视为一个操作数)
-
首先先利用括号划分操作数和运算符
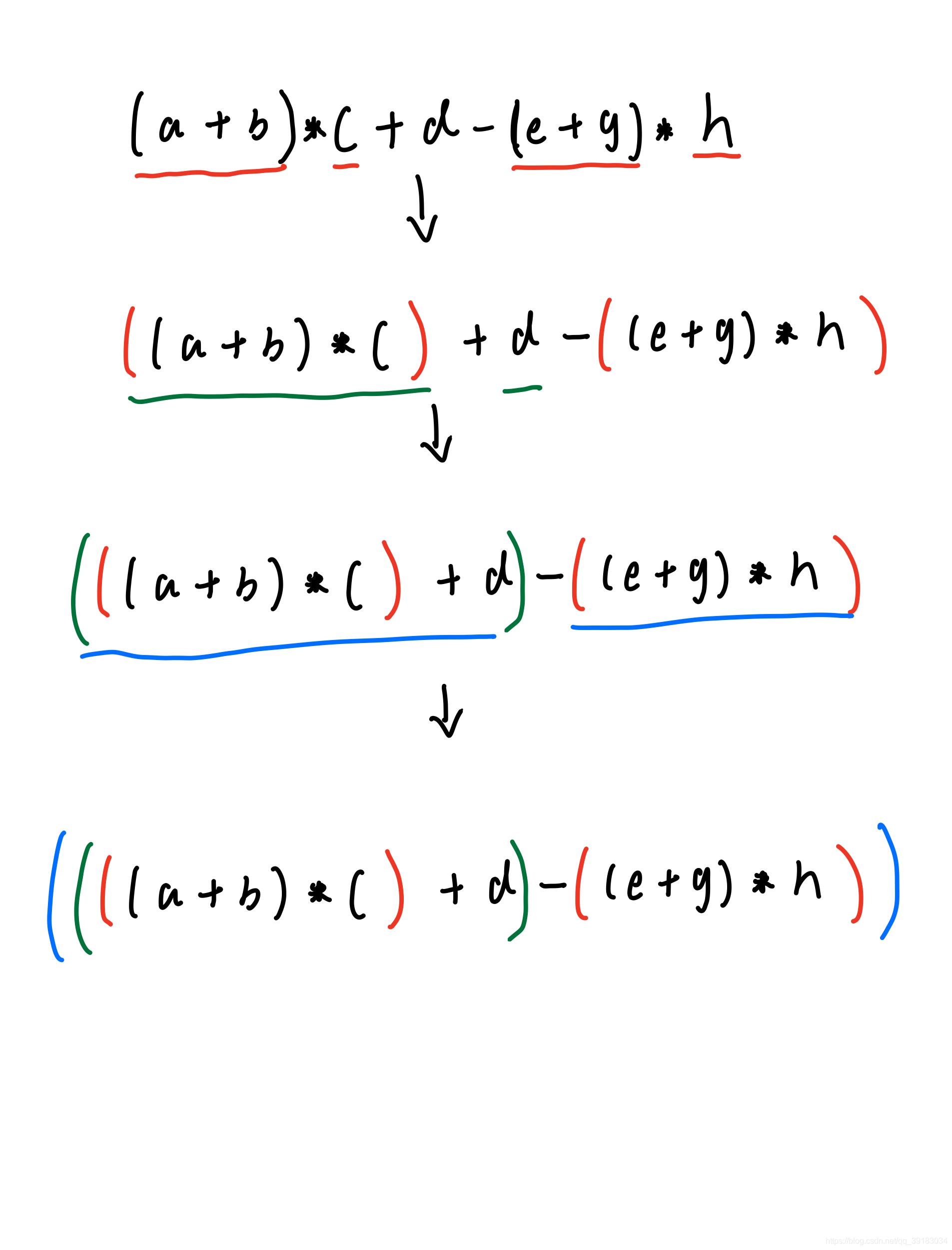
-
接着将运算符移出到所在括号外部(只需要移动到该运算符原来所在的括号前面就可以了,不要一次移动多层)

转化为后缀表达式时,只需要移动到括号后面就可以了,由于非常简单,这里就不演示了,结果在最上面
②:前缀转中缀和后缀转中缀
原则:前缀表达式是将中缀表达式运算符放在前面,因此转回时需要从后向前扫描前缀表达式,每遇到两个操作数一个运算符就把运算符放到两个操作数中间,有的时候可能会连续遇到三个及以上的操作数,这时就不要管后面的操作数了,你只需要向前找,一直找到运算符然后结合后面的两个操作数组合在一起

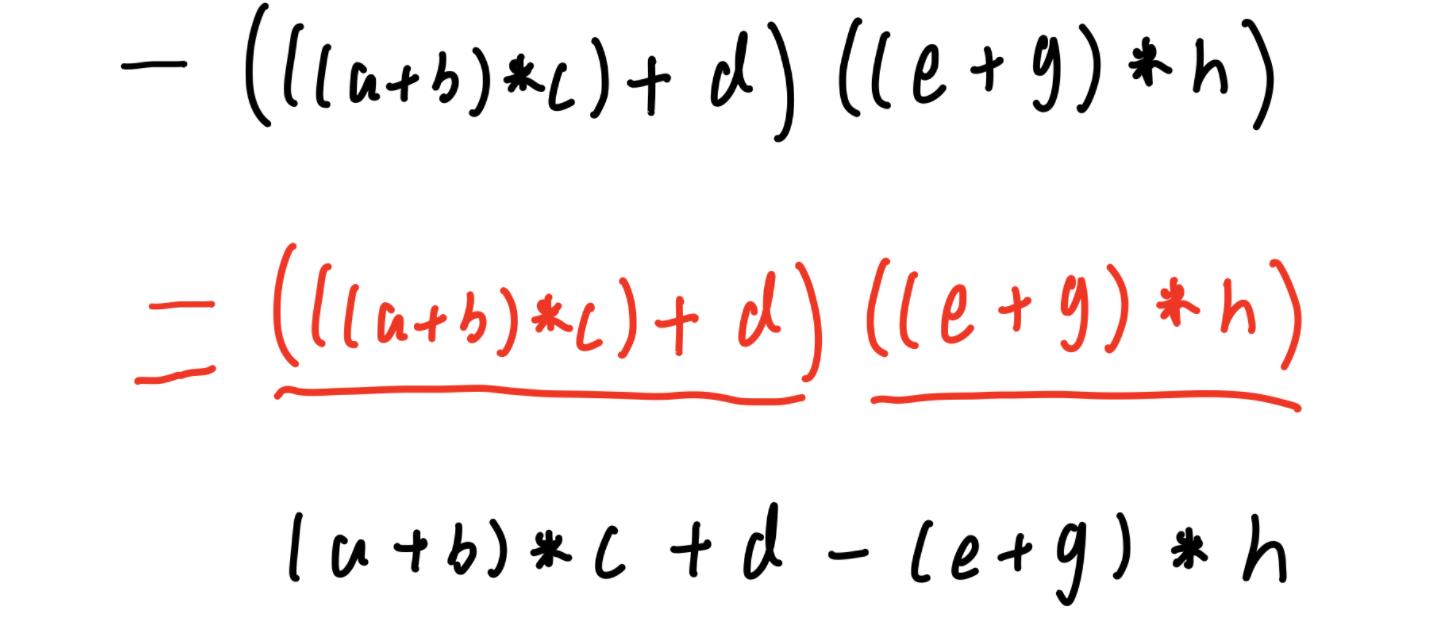
对于后缀转中缀,和前缀转中缀实则是一样的,只不过后缀转中缀的时候需要从前向后扫描
B:使用代码实现
这里用栈实现表达式转换主要指的是中缀转前缀或者后缀,其他形式的表达式的转换没有意义,因为转为前缀和后缀的目的就是让计算机进行求值由于C语言中处理栈比较麻烦,所以这里采用C++,省去一些造轮子的步骤
①:中缀转后缀
中缀式转后缀式需要两个栈完成,然后从后向前扫描中缀表达式,这里先不讨论怎样入栈,大家可以跟着过程走一遍,后面再总结。不过记住:所有的操作数入S1栈,所有的括号和运算符入S2栈
- 如下,S2空,第一个扫描到了左括号,遇到左括号直接入栈
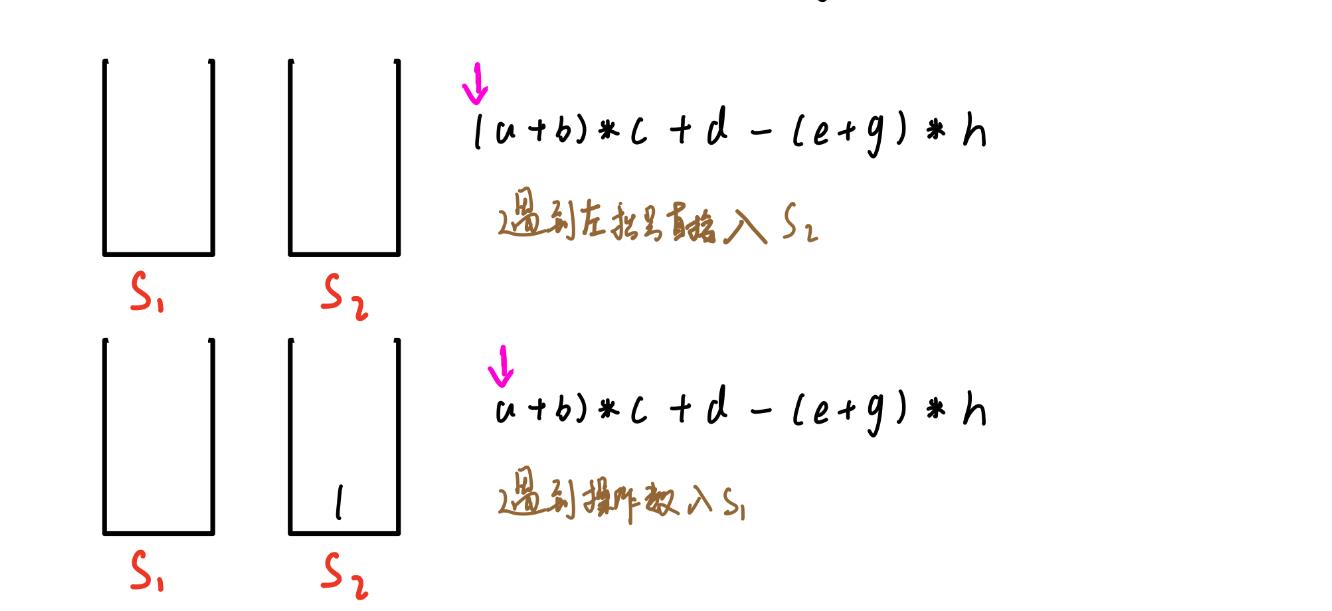
- 接着扫描到了操作数a,直接入S1

- 接着扫描到了“+”号,此时S2栈顶元素为左括号,任何运算符在S2栈顶元素为左括号时直接入栈

- 继续进行,扫描到
b直接入S1。然后扫描到了右括号,当扫描到右括号时将S2中从栈顶元素到左括号(只取一个)之间的元素依次出S2,入S1,但是左括号忽略掉,也就是不要了

- 接着扫描到
“*”,入S2,然后扫描到操作数“c”,入S1。接着扫描到“+”,由于扫描到的元素运算符优先级小于等于S2栈顶元素运算符的优先级,故将栈顶元素出S2入S1,然后接着再与新的栈顶元素比较,如果还是小于等于重复上述步骤,如果是大于则直接入S2,这里由于“*”出栈后,S2为空,故直接入S2
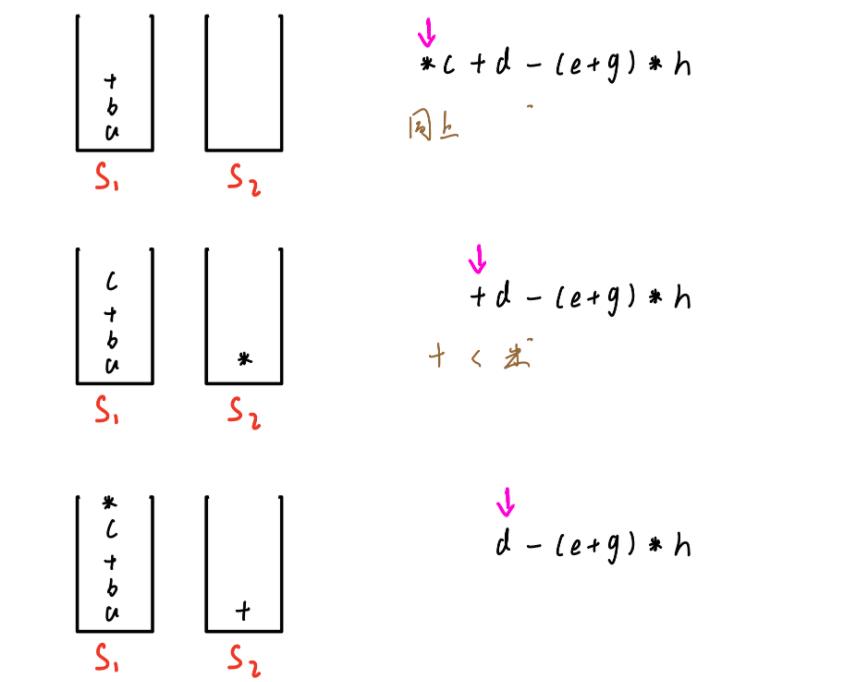
- 接着再入操作数
d,然后来到运算符-,由于扫描到的运算符的优先级小于等于栈顶元素优先级,故出S2入S1
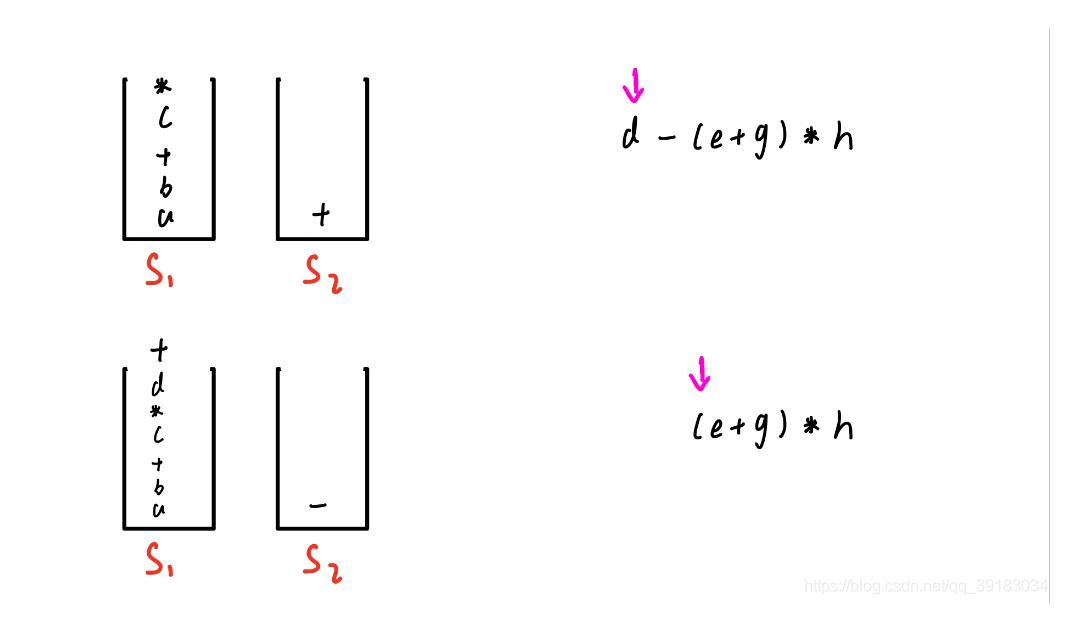
剩余部分就不再演示了,此时大家观察S1栈,是不是已经有了后缀式的雏形了呢
总结:所有操作数入S1,所有左括号和运算符入S2,遇到右括号时S2出,遇到运算符需要进行比较优先级,具体解释如下
- 如果S2栈顶元素为左括号,任何运算符无条件入S2
- 如果扫描到了右括号,那么把S1中从栈顶元素到左括号(只取一个)之间的元素依次出S2,入S1(左括号不入,直接丢弃)
- 如果扫描的运算符的优先级要小于等于S2栈顶元素运算符的优先级,那么将栈顶运算符出S2入S1,然后再与新的栈顶元素比较,如果还是小于等于则重复,如果成了大于则直接入S2
代码
#include <iostream>
#include <stack>
#include <string>
using namespace std;
int getpriority(char c)//优先级判断
{
if (c == '+' || c == '-')
{
return -1;//加减优先级小
}
else
{
return 1;//乘除优先级大
}
}
void convert(string& express, stack<char>& s1, stack<char>& s2)
{
int i = 0;
while (express[i] != '\\0')//扫描中缀表达式
{
if ('0' <= express[i] && express[i] >= '9')//如果扫描到了操作数,直接入s1
{
s1.push(express[i++]);
}
else if (express[i] == '(')//如果扫描到了左括号,直接入s2
{
s2.push(express[i++]);
}
else if (express[i] == '+' || express[i] == '-' || express[i] == '*' || express[i] == '/')//扫描到运算符进行优先级判断
{
if (s2.empty() || s2.top() == '(' || getpriority(express[i]) > getpriority(s2.top()))//如果此时S2为空或者栈顶元素为左括号,或者扫描到的运算符优先级大于栈顶运算符优先级,则S2
{
s2.push(express[i++]);
}
else//反之优先级如果是小于等于的话,那么就要把运算符出栈然后入S1
{
char temp = s2.top();
s2.pop();
s1.push(temp);
}
}
else if (express[i] == ')')//最后一种情况就是扫描到了右括号,那么就把S2从栈顶到左括号的元素依次出栈入栈
{
while (s2.top() != '(')
{
char temp = s2.top();
s2.pop();
s1.push(temp);
}
//注意最后停止循环的时候S2的栈顶元素是左括号,但是不要把左括号入栈,所以直接丢掉左括号
s2.pop();
i++;//不要忘记后移
}
}
while (!(s2.empty()))//如果S2没有空,那么依次出S2,入S1
{
char temp = s2.top();
s2.pop();
s1.push(temp);
}
}
int main()
{
stack<char> s1;//结果栈,入操作数
stack<char> s2;//辅助栈,入运算符和括号
stack<char> result;//输出用
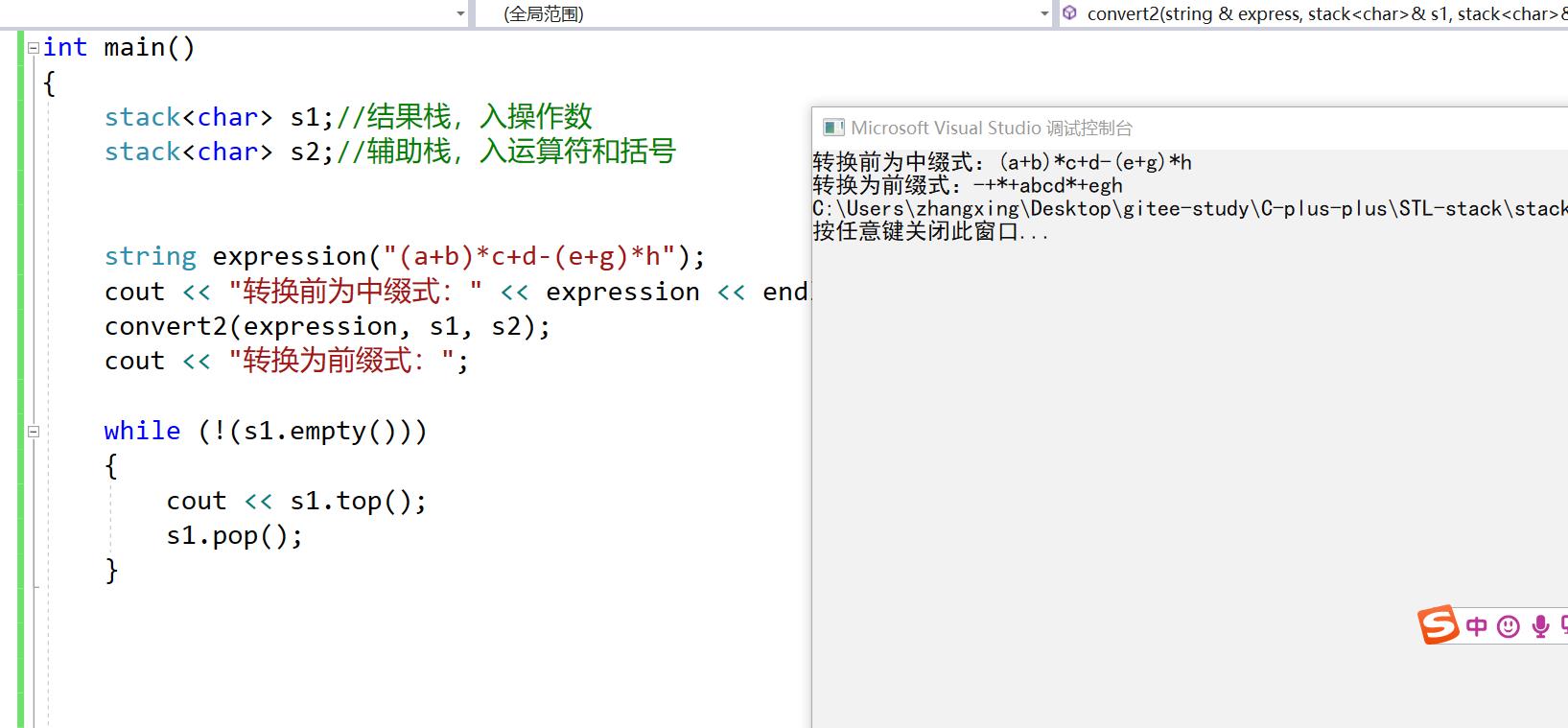
string expression("(a+b)*c+d-(e+g)*h");
cout << "转换前为中缀式:" << expression << endl;
convert(expression, s1, s2);
cout << "转换为中缀式:";
while (!(s1.empty()))
{
char temp = s1.top();
s1.pop();
result.push(temp);
}
while (!(result.empty()))
{
cout << result.top();
result.pop();
}
}
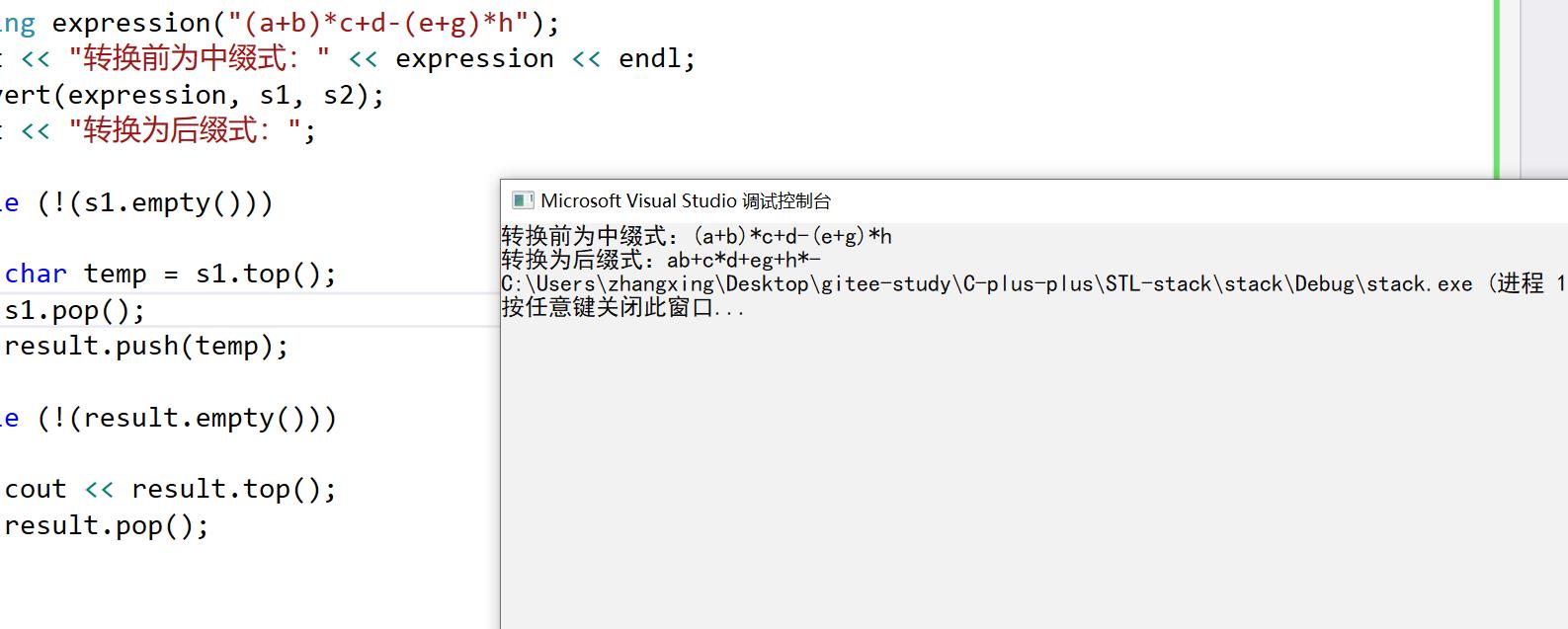
②:中缀转前缀
中缀转前缀和中缀转后缀基本一致,不同点如下
- 扫描时从后向前扫描中缀式
- 遇到右括号直接入栈,遇到左括号进行出栈
- 扫描到的运算符优先级如果大于等于栈顶运算符优先级,直接入栈
void convert2(string& express, stack<char>& s1, stack<char>& s2)//中缀转前缀
{
int i = express.size()-1;
while (i>=0)//扫描中缀表达式
{
if ('a' <= express[i] && express[i] <= 'z')//如果扫描到了操作数,直接入s1
{
s1.push(express[i--]);
}
else if (express[i] == ')')//如果扫描到了右括号,直接入s2
{
s2.push(express[i--]);
}
else if (express[i] == '+' || express[i] == '-' || express[i] == '*' || express[i] == '/')//扫描到运算符进行优先级判断
{
if (s2.empty() || s2.top() == ')' || getpriority(express[i]) >= getpriority(s2.top()))//如果此时S2为空或者栈顶元素为左括号,或者扫描到的运算符优先级大于等于栈顶运算符优先级,则入S2
{
s2.push(express[i--]);
}
else//反之优先级如果是大于等于的话,那么就要把运算符出栈然后入S1
{
char temp = s2.top();
s2.pop();
s1.push(temp);
}
}
else if (express[i] == '(')//最后一种情况就是扫描到了左括号,那么就把S2从栈顶到右括号的元素依次出栈入栈
{
while (s2.top() != ')')
{
char temp = s2.top();
s2.pop();
s1.push(temp);
}
//注意最后停止循环的时候S2的栈顶元素是右括号,但是不要把右括号入栈,所以直接丢掉右括号
s2.pop();
i--;//不要忘记后移
}
}
while (!(s2.empty()))//如果S2没有空,那么依次出S2,入S1
{
char temp = s2.top();
s2.pop();
s1.push(temp);
}
}
(2)表达式求值
我们转换表达式的目的就在于让计算机实现表达式的求值,或者说,计算机是不认识也不清楚中缀式的含义的,只有人能读懂,但是我们转换为前缀或者后缀后却可以借助栈的性质来完成计算
这里我们就以LeetCode 150:逆波兰式求值,也就是后缀表达式求值为例,前缀式基本一致
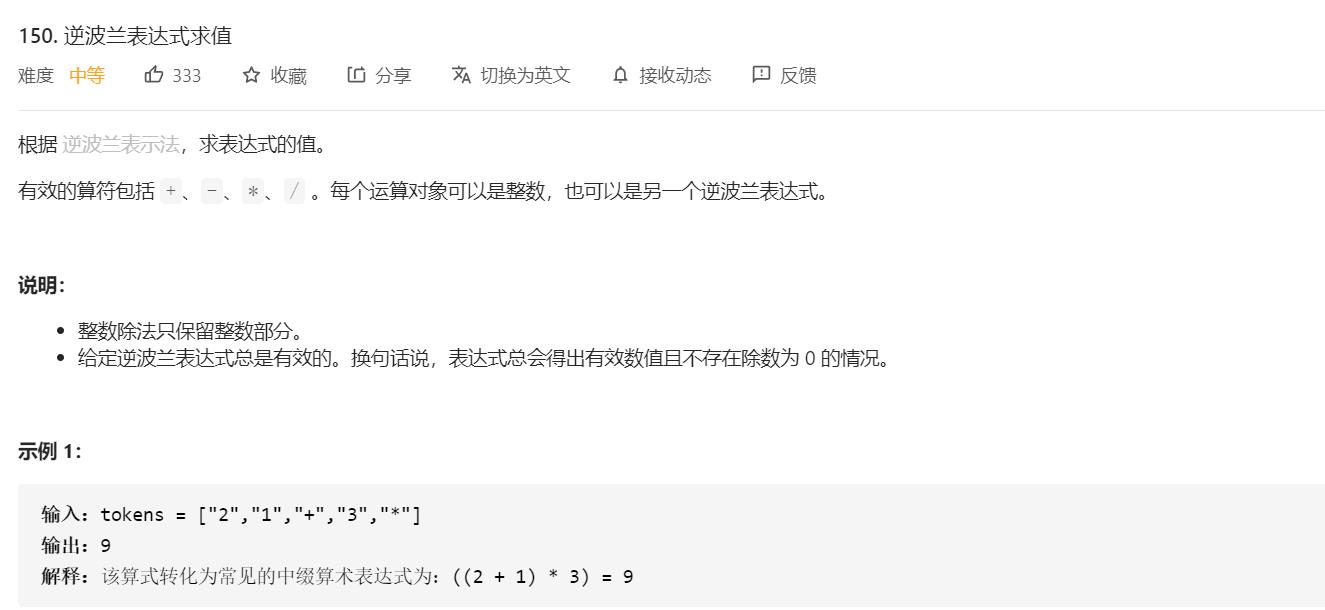
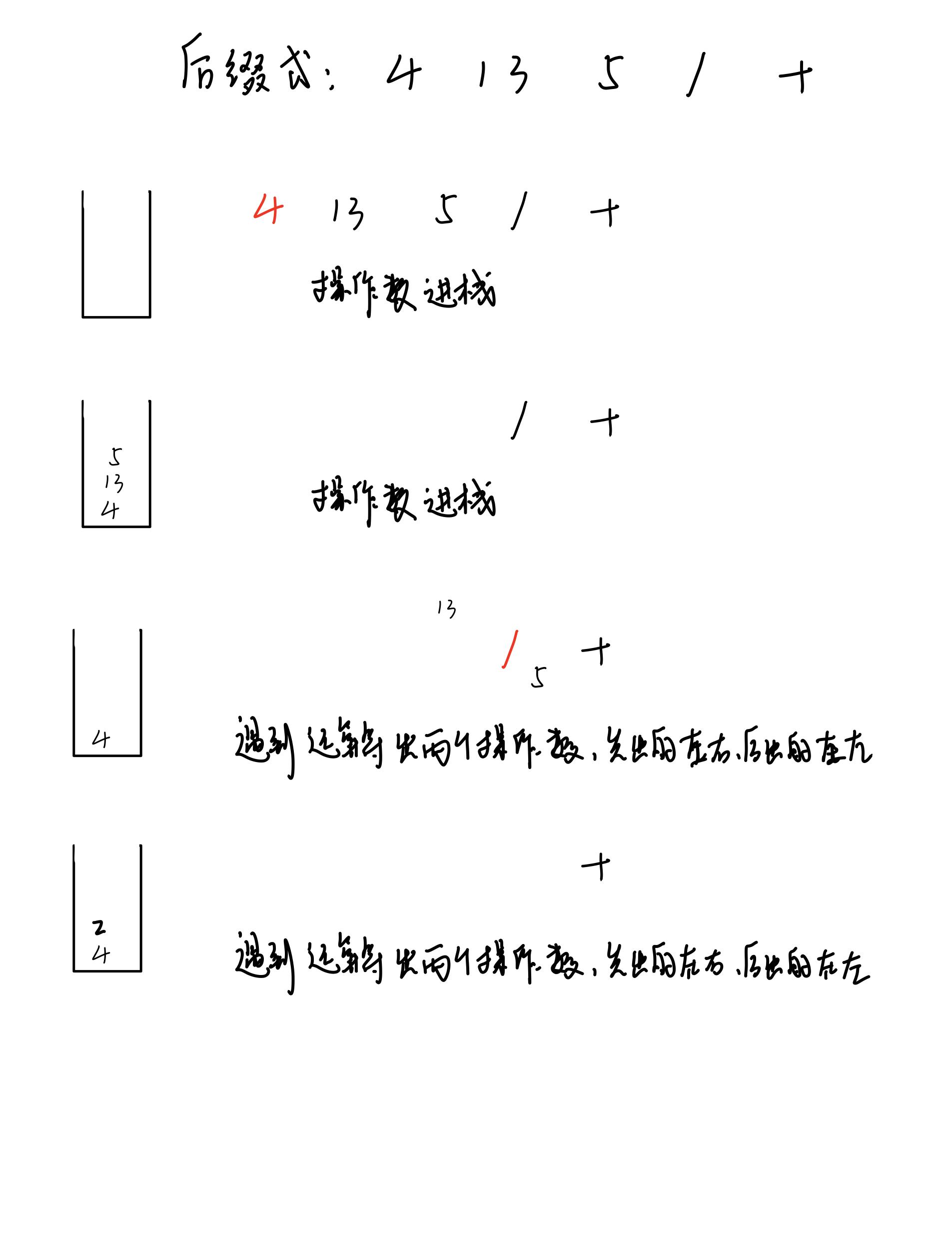
求解时,准备一个栈,从左向右扫描后缀表达式,遇到操作数就入栈,遇到运算符则出栈两个操作数,先出栈的作为右操作数,后出栈的作为左操作数,然后运算之后把结果继续压入栈内,重复以上步骤,最后栈中的栈顶元素就是结果
class Solution {
public:
void calculate(int& opnd1,string& op,int& opnd2,int& result)//计算
{
if(op=="+")
result=opnd1+opnd2;
if(op=="-")
result=opnd1-opnd2;
if(op=="*")
result=opnd1*opnd2;
if(op=="/")
result=opnd1/opnd2;
}
int evalRPN(vector<string>& tokens)
{
stack<int> ret;//结果栈
for(int i=0;i<tokens.size();i++)
{
if(tokens[i].size()==1 && (tokens[i] =="+" || tokens[i] =="-" || tokens[i] =="*" || tokens[i] =="/" ))//运算符
{
int opnd1,opnd2,result;//两个操作数和结果
string op;//运算符
op=tokens[i];//运算符
opnd2=ret.top();
ret.pop();//先出来的是右操作数
opnd1=ret.top();
ret.pop();//后出来的是左操作数
calculate(opnd1,op,opnd2,result);
ret.push(result);//计算结果仍然压入栈
}
else//操作数
{
int temp=atoi(tokens[i].c_str());
ret.push(temp);
}
}
return ret.top();//栈顶元素是结果
}
};
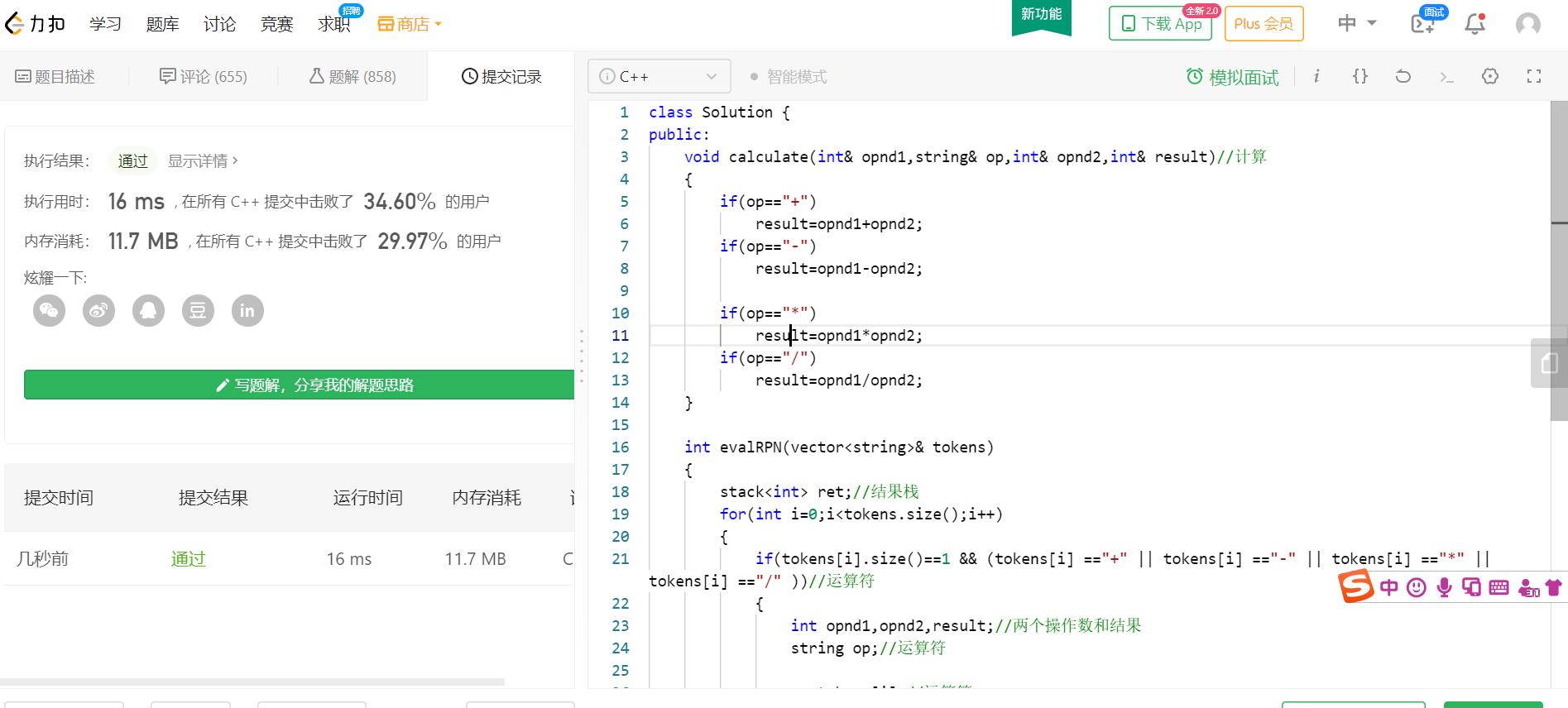
前缀表达式和这个基本一致,不同点就是要从后向前扫描,然后先出栈的是左操作数,后出栈的是右操作数
以上是关于(王道408考研数据结构)第三章栈和队列-第三节1:栈的应用之括号匹配问题和表达式问题(前缀中缀和后缀)的主要内容,如果未能解决你的问题,请参考以下文章
(王道408考研数据结构)第三章栈和队列-第四节:特殊矩阵压缩方式
(王道408考研数据结构)第三章栈和队列-第二节:队列基本概念顺序栈和链栈基本操作
(王道408考研数据结构)第三章栈和队列-第一节:栈基本概念顺序栈和链栈基本操作
(王道408考研操作系统)第二章进程管理-第三节7:经典同步问题之多生产者与多消费者问题