点云配准1-ICP算法 手写代码实现

Posted 行码阁119

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了点云配准1-ICP算法 手写代码实现相关的知识，希望对你有一定的参考价值。

一、声明：

本人作为初学者，才开始接触点云配准这一块，如有错误地方，望大家指出，我将及时修改，共同进步。

二、需提前知道理论知识

代码只实现ICP算法中理论部分，其他部分后续实现。

对于ICP算法了解不够熟悉，推荐其下博客（尤其是第二篇）：

三维点云配准 -- ICP 算法原理及推导 - 知乎 (zhihu.com)

SLAM常见问题(四)：求解ICP，利用SVD分解得到旋转矩阵 | RealCat (gitee.io)

对于奇异值分解不够熟悉，可以看一下：

奇异值分解（SVD） - 知乎 (zhihu.com)

三、ICP代码算法实现步骤

step1. 计算两组匹配点的质心，每个点的位置为：{},{}：

 ， 

step2. 得到去质心的点集：

step3. 根据公式算其奇异分解钱的3x3的举证：

其中：X为去除质心的源点云矩阵，Y为去除质心的目标点云矩阵

step4. 对S进行SVD 奇异值分解，得到旋转矩阵R：

其中V求算公式为(为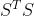特征向量组成的矩阵)：

其中U求算公式为(为特征向量组成的矩阵)：

step5. 计算平移量：

四、代码实现（按照步骤三实现）

1、主函数（如果你要修改初始点云的位置，可以修改main函数下第二个for）：

int main()
{
	MatrixXd input(n,m);
	MatrixXd output(n,m);
	//给数组赋值
	for (int i = 0; i < m; i++)
	{
		input(0,i) = 1024 * rand() / (RAND_MAX + 1.0f);
		input(1,i) = 1024 * rand() / (RAND_MAX + 1.0f);
		input(2,i) = 1024 * rand() / (RAND_MAX + 1.0f);
		output(0, i) = input(0, i);
		output(1, i) = input(1, i);
		output(2, i) = input(2, i);
	}
	//打印初始点云
	cout << input << endl;

	//将点云的x坐标进行先前移动0.7个坐标
	for (int i = 0; i < m; i++)
	{
		output(0,i) = output(0,i) + 0.7f;
	}
	cout << "-----------------" << endl;
	//打印出输出点云
	cout << output << endl;
	//icp算法
	icp(input, output);
}

 1.1 结果：

目标点云：
1.28125 828.125 358.688   764.5 727.531
577.094 599.031 917.438 178.281 525.844
197.938 491.375 842.562 879.531 311.281
向X轴平移0.7f个单位的点云：
1.98125 828.825 359.387   765.2 728.231
577.094 599.031 917.438 178.281 525.844
197.938 491.375 842.562 879.531 311.281

2、计算矩阵的质心函数

MatrixXd computer3DCentroid(MatrixXd& input)
{
	float sum_x = 0;
	float sum_y = 0;
	float sum_z = 0;
	for (int i = 0; i < m ; i++)
	{
		sum_x += input(0, i);
		sum_y += input(1, i);
		sum_z += input(2, i);
	}
	sum_x = sum_x / m;
	sum_y = sum_y / m;
	sum_z = sum_z / m;
	MatrixXd Centroid(1,3);
	Centroid << sum_x, sum_y, sum_z;
	return Centroid;
}

2.1 结果：

目标矩阵的质心：
536.025 559.537 544.537
经旋转和平移矩阵的质心：
536.725 559.537 544.537

3、对目标点云矩阵和源点云矩阵去质心并且计算旋转矩阵R和平移量T

		//计算目标矩阵的质心并去质心
		MatrixXd inCenterI = computer3DCentroid(Target);
		MatrixXd myinCenterI = inCenterI.transpose() * Sing;
		MatrixXd  MyInCenterI = Target - myinCenterI;
		//计算源矩阵的质心并去质心
		MatrixXd inCenterO = computer3DCentroid(Trans);
		MatrixXd myinCenterO = inCenterO.transpose() * Sing;
		MatrixXd MyInCenterO = Trans - myinCenterO;
		//计算R
		MatrixXd H = MyInCenterO * MyInCenterI.transpose();
		MatrixXd  U = H * H.transpose();
		EigenSolver<MatrixXd> es(U);
		MatrixXd  Ue = es.pseudoEigenvectors();
		MatrixXd V = H.transpose() *H;
		EigenSolver<MatrixXd> es1(V);
		MatrixXd  Ve = es1.pseudoEigenvectors();
		R = Ve * Ue.transpose();
		MatrixXd  gR = MatrixXd::Identity(n, n);
		gR(2, 2) = R.determinant();
		R = Ve *gR * Ue.transpose();
		cout << "旋转矩阵R为：" << endl;
		cout << R << endl;
		cout << "---------------------这里行列式一定要为1-----------------" << endl;
		std::cout << "旋转矩阵R行列式： " << R.determinant() << std::endl;
		cout << "---------------------------------------------------------" << endl;
		//计算T
		T = inCenterI - R * inCenterO;
		cout << "转移量T:" << endl << T << endl;
		T = T.transpose() * Sing;
		cout << "转移量T矩阵：" << endl << T << endl;

3.1 结果

旋转矩阵R为：
           1 -8.57647e-15 -7.82707e-15
 8.88178e-15            1 -3.88578e-15
 7.82707e-15  3.83027e-15            1
---------------------这里行列式一定要为1-----------------
旋转矩阵R行列式： 1
---------------------------------------------------------
转移量T:
  -0.699951 2.27374e-13 2.27374e-13
转移量T矩阵：
  -0.699951   -0.699951   -0.699951   -0.699951   -0.699951
2.27374e-13 2.27374e-13 2.27374e-13 2.27374e-13 2.27374e-13
2.27374e-13 2.27374e-13 2.27374e-13 2.27374e-13 2.27374e-13

4、进行误差计算：

	Trans = R * Trans + T;
	err = Trans - Target;
	err2 = (err.cwiseProduct(err)).sum();
	cout << err2 << endl;
1.19151e-08

5、打印最后旋转的举证：

 1.2813 828.125 358.688   764.5 727.531
577.094 599.031 917.438 178.281 525.844
197.938 491.375 842.563 879.531 311.281

五、完整代码

# include<iostream>
#include <Eigen/Dense>
#include <Eigen/Eigenvalues>
using namespace Eigen;
using namespace std;

# define m 5
# define n 3
//计算质心的函数
MatrixXd computer3DCentroid(MatrixXd& input)
{
	float sum_x = 0;
	float sum_y = 0;
	float sum_z = 0;
	for (int i = 0; i < m ; i++)
	{
		sum_x += input(0, i);
		sum_y += input(1, i);
		sum_z += input(2, i);
	}
	sum_x = sum_x / m;
	sum_y = sum_y / m;
	sum_z = sum_z / m;
	MatrixXd Centroid(1,3);
	Centroid << sum_x, sum_y, sum_z;
	return Centroid;
}


void icp(MatrixXd& Target, MatrixXd& Source)
{
	MatrixXd R = MatrixXd::Identity(n, n);
	cout << R << endl;
	MatrixXd T(n, m);
	MatrixXd Trans = R * Source + T;
	MatrixXd err = Trans - Target;
	float err2 = (err.cwiseProduct(err)).sum();
	while (err2 > 0.5)
	{
		MatrixXd Sing(1, 5);
		Sing << 1, 1, 1,1,1;
		//计算目标矩阵的质心并去质心
		MatrixXd inCenterI = computer3DCentroid(Target);
		MatrixXd myinCenterI = inCenterI.transpose() * Sing;
		MatrixXd  MyInCenterI = Target - myinCenterI;
		//计算源矩阵的质心并去质心
		MatrixXd inCenterO = computer3DCentroid(Trans);
		MatrixXd myinCenterO = inCenterO.transpose() * Sing;
		MatrixXd MyInCenterO = Trans - myinCenterO;
		//计算R
		MatrixXd H = MyInCenterO * MyInCenterI.transpose();
		MatrixXd  U = H * H.transpose();
		EigenSolver<MatrixXd> es(U);
		MatrixXd  Ue = es.pseudoEigenvectors();
		MatrixXd V = H.transpose() *H;
		EigenSolver<MatrixXd> es1(V);
		MatrixXd  Ve = es1.pseudoEigenvectors();
		R = Ve * Ue.transpose();
		MatrixXd  gR = MatrixXd::Identity(n, n);
		gR(2, 2) = R.determinant();
		R = Ve *gR * Ue.transpose();
		cout << "旋转矩阵R为：" << endl;
		cout << R << endl;
		cout << "---------------------这里行列式一定要为1-----------------" << endl;
		std::cout << "旋转矩阵R行列式： " << R.determinant() << std::endl;
		cout << "---------------------------------------------------------" << endl;
		//计算T
		T = inCenterI - R * inCenterO;
		cout << "转移量T:" << endl << T << endl;
		T = T.transpose() * Sing;
		cout << "转移量T矩阵：" << endl << T << endl;
		Trans = R * Trans + T;
		err = Trans - Target;
		err2 = (err.cwiseProduct(err)).sum();
		cout <<"误差为：" << err2 << endl;
	}
	cout << "Trans:" << endl;
	cout << Trans << endl;
	
}
int main()
{
	MatrixXd input(n,m);
	MatrixXd output(n,m);
	//给数组赋值
	for (int i = 0; i < m; i++)
	{
		input(0,i) = 1024 * rand() / (RAND_MAX + 1.0f);
		input(1,i) = 1024 * rand() / (RAND_MAX + 1.0f);
		input(2,i) = 1024 * rand() / (RAND_MAX + 1.0f);
		output(0, i) = input(0, i);
		output(1, i) = input(1, i);
		output(2, i) = input(2, i);
	}
	//打印初始点云
	cout << "目标点云：" << endl;
	cout << input << endl;
	//将点云的x坐标进行先前移动0.7个坐标
	for (int i = 0; i < m; i++)
	{
		output(0,i) = output(0,i) + 0.7f;
		output(1, i) = output(1, i) + 0.1f;
	}

	//打印出输出点云
	cout << "向X轴平移0.7f个单位的点云：" << endl;
	cout << output << endl;
	//icp算法
	icp(input, output);
}

六点：补充：

如果我们将main函数下第二个for循环改为中将点云y坐标重新赋值且向y方向移动500f,会发现ICP将不收敛，所以其缺点较为明显，需要一个初配准，且容易陷入局部最优。

int main()
{
	MatrixXd input(n,m);
	MatrixXd output(n,m);
	//给数组赋值
	for (int i = 0; i < m; i++)
	{
		input(0,i) = 1024 * rand() / (RAND_MAX + 1.0f);
		input(1,i) = 1024 * rand() / (RAND_MAX + 1.0f);
		input(2,i) = 1024 * rand() / (RAND_MAX + 1.0f);
		output(0, i) = input(0, i);
		output(1, i) = input(1, i);
		output(2, i) = input(2, i);
	}
	//打印初始点云
	cout << "目标点云：" << endl;
	cout << input << endl;
	//将点云的x坐标进行先前移动0.7个坐标
    //点云y坐标重新赋值且向y方向移动500f
	for (int i = 0; i < m; i++)
	{
		output(0,i) = output(0,i) + 0.7f;
		output(1, i) = output(0, i) + 0.7f;
	}

	//打印出输出点云
	cout << "向X轴平移0.7f个单位的点云：" << endl;
	cout << output << endl;
	//icp算法
	icp(input, output);
}

以上是关于点云配准1-ICP算法 手写代码实现的主要内容，如果未能解决你的问题，请参考以下文章

MATLAB怎么实现两个点云的配准

点云配准(Registration)算法——以PCL为例

点云配准 -辅助知识 最小二乘法代码实现拟合曲线（C++）

3D，点云拼接2

PCL学习总结点云配准算法之ICP系列

ICP点云配准原理及优化