点云配准 -辅助知识 最小二乘法代码实现拟合曲线（C++）
Posted 行码阁119
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了点云配准 -辅助知识 最小二乘法代码实现拟合曲线（C++）相关的知识，希望对你有一定的参考价值。
一、原理讲解
通过实验获得一些列的观测数值(假设为三个)：
其每个样本观测值对应的精确值为：
这里假设其观测值对应的准确值为：
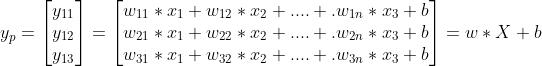
上面矩阵计算公式可以等价于：
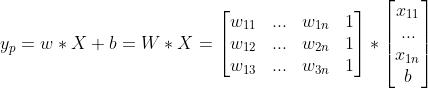
其误差计算公式：
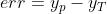
其平方误差计算公式：
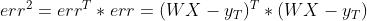
由于这是误差公式关于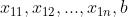
的平方公式，所以根据要达到误差最小，既是极点，对其求导，令其等于0：
可知：
此时，系数就找到了，带入就可：
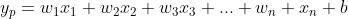
二、代码实现
2.1 最小二乘拟合正弦函数
代码复现的统计学第一章-最小二乘拟合正弦函数，正则化，其官方python代码为：
#coding:utf-8
import numpy as np
import scipy as sp
from scipy.optimize import leastsq
import matplotlib.pyplot as plt
# 目标函数
def real_func(x):
return np.sin(2*np.pi*x)
# 多项式
def fit_func(p, x):
f = np.poly1d(p)
# print('f=',f)
return f(x)
# 残差
def residuals_func(p, x, y):
ret = fit_func(p, x) - y
return ret
# 十个点
x = np.linspace(0, 1, 10)
x_points = np.linspace(0, 1, 1000)
# 加上正态分布噪音的目标函数的值
y_ = real_func(x)
y = [np.random.normal(0, 0.1) + y1 for y1 in y_]
def fitting(M=0):
"""
M 为 多项式的次数
"""
# 随机初始化多项式参数
p_init = np.random.rand(M + 1)
# 最小二乘法
p_lsq = leastsq(residuals_func, p_init, args=(x, y))
print('Fitting Parameters:', p_lsq[0])
#
# 可视化
plt.plot(x_points, real_func(x_points), label='real')
plt.plot(x_points, fit_func(p_lsq[0], x_points), label='fitted curve')
plt.plot(x, y, 'bo', label='noise')
plt.legend()
plt.show()
return p_lsq
# M=0
p_lsq_0 = fitting(M=0)
# M=1
p_lsq_1 = fitting(M=1)
# M=3
p_lsq_3 = fitting(M=3)
# M=9
p_lsq_9 = fitting(M=9)其运行结果图：
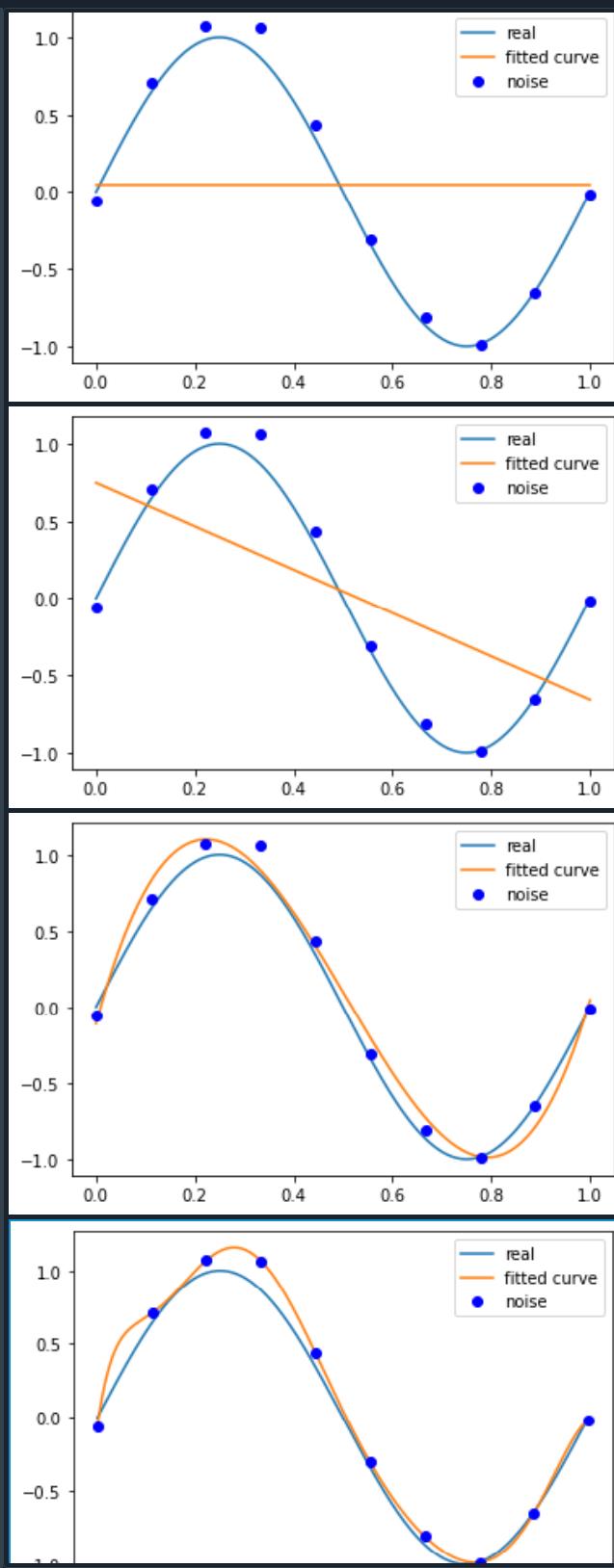
2.2 c++实现拟合正弦曲线（对应上诉代码M = 10）
头函数：
# include<iostream>
# include<Eigen/Dense>
# include<math.h>
# include<Eigen/Eigenvalues>
using namespace std;
using namespace Eigen;生成原理所讲矩阵w,x,yt
//生成观测值
MatrixXd x(20, 10);
//目标值
MatrixXd y(20, 1);
//权重值
MatrixXd w(10, 1) ;计算误差函数（）：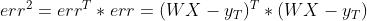
MatrixXd errCount(MatrixXd y_p, MatrixXd y_t)
MatrixXd err = (y_p - y_t);
MatrixXd myerr = err.transpose() * err;
return myerr;
关键部分（原理）实现：
MatrixXd leastsq(MatrixXd y_p, MatrixXd y_t, MatrixXd x, MatrixXd w)
MatrixXd err = errCount(y_p, y_t);
if (err.sum() > 0.1)
w = (x.transpose() * x).inverse() * x.transpose() * y;
y_p = x * w;
err = errCount(y_p, y_t);
cout << err.sum() << endl;
return w;
由于官方函数，说明当M=10(多项式的系数)效果最好，固然复现构造函数（只有一个观测值x）:
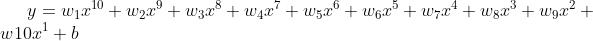
for (int i = 0; i < 20; i++)
x(i, 9) = 1;
x(i, 8)=0.25 + sum;
x(i, 7) = x(i, 8) * x(i, 8);
x(i, 6) = x(i, 8) * x(i, 8) * x(i, 8);
x(i, 5) = x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8);
x(i, 4) = x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8);
x(i, 3) = x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8);
x(i, 2) = x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8);
x(i, 1) = x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8)*x(i, 8);
x(i, 0) = x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8)*x(i, 8)*x(i, 8);
y(i, 0) = sin(x(i,8)*3.14);
sum = sum + 0.25;
w:
0 0 0 0 0 0 0 0 0 1
3.8147e-06 1.52588e-05 6.10352e-05 0.000244141 0.000976562 0.00390625 0.015625 0.0625 0.25 1
0.00195312 0.00390625 0.0078125 0.015625 0.03125 0.0625 0.125 0.25 0.5 1
0.0750847 0.100113 0.133484 0.177979 0.237305 0.316406 0.421875 0.5625 0.75 1
1 1 1 1 1 1 1 1 1 1
7.45058 5.96046 4.76837 3.8147 3.05176 2.44141 1.95312 1.5625 1.25 1
38.4434 25.6289 17.0859 11.3906 7.59375 5.0625 3.375 2.25 1.5 1
153.937 87.9639 50.2651 28.7229 16.4131 9.37891 5.35938 3.0625 1.75 1
512 256 128 64 32 16 8 4 2 1
1477.89 656.841 291.929 129.746 57.665 25.6289 11.3906 5.0625 2.25 1
3814.7 1525.88 610.352 244.141 97.6562 39.0625 15.625 6.25 2.5 1
8994.86 3270.86 1189.4 432.51 157.276 57.1914 20.7969 7.5625 2.75 1
19683 6561 2187 729 243 81 27 9 3 1
40453 12447.1 3829.87 1178.42 362.591 111.566 34.3281 10.5625 3.25 1
78815.6 22518.8 6433.93 1838.27 525.219 150.062 42.875 12.25 3.5 1
146650 39106.6 10428.4 2780.91 741.577 197.754 52.7344 14.0625 3.75 1
262144 65536 16384 4096 1024 256 64 16 4 1
452377 106442 25045.1 5892.96 1386.58 326.254 76.7656 18.0625 4.25 1
756681 168151 37366.9 8303.77 1845.28 410.062 91.125 20.25 4.5 1
1.23096e+06 259149 54557.6 11485.8 2418.07 509.066 107.172 22.5625 4.75 1yt:
0 0.706825 1 0.707951 0.00159265 -0.705698 -0.999997 -0.709075 -0.0031853 0.704568 0.999992 0.710197 0.00477794 -0.703437 -0.999984 -0.711317 -0.00637057 0.702304 0.999974 0.712436
原始y_p:
1 1.33333 1.99805 3.77475 10 33.2529 113.33 357.853 1023 2659.41 6357.16 14134.2 29524 58431.6 110341 199977 349525 591569 972875 1.55921e+06变换过后：
精确值
0 0.706825 1 0.707951 0.00159265 -0.705698 -0.999997 -0.709075 -0.0031853 0.704568 0.999992 0.710197 0.00477794 -0.703437 -0.999984 -0.711317 -0.00637057 0.702304 0.999974 0.712436
变换后的y_p:
0.0103961 0.658876 1.06156 0.724083 -0.0521667 -0.743825 -0.969841 -0.649122 0.0135521 0.657116 0.942181 0.709952 0.0648353 -0.655788 -1.02993 -0.781023 -0.000910797 0.785843 0.94112 0.7246962.3 完整代码
# include<iostream>
# include<Eigen/Dense>
# include<math.h>
# include<Eigen/Eigenvalues>
using namespace std;
using namespace Eigen;
//生成观测值
MatrixXd x(20, 10);
//目标值
MatrixXd y(20, 1);
//权重值
MatrixXd w(10, 1) ;
MatrixXd errCount(MatrixXd y_p, MatrixXd y_t)
MatrixXd err = (y_p - y_t);
MatrixXd myerr = err.transpose() * err;
return myerr;
MatrixXd leastsq(MatrixXd y_p, MatrixXd y_t, MatrixXd x, MatrixXd w)
MatrixXd err = errCount(y_p, y_t);
if (err.sum() > 0.1)
w = (x.transpose() * x).inverse() * x.transpose() * y;
y_p = x * w;
err = errCount(y_p, y_t);
cout << err.sum() << endl;
return w;
int main()
float sum=-0.25;
//给观测值和准确值赋值
for (int i = 0; i < 20; i++)
x(i, 9) = 1;
x(i, 8)=0.25 + sum;
x(i, 7) = x(i, 8) * x(i, 8);
x(i, 6) = x(i, 8) * x(i, 8) * x(i, 8);
x(i, 5) = x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8);
x(i, 4) = x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8);
x(i, 3) = x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8);
x(i, 2) = x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8);
x(i, 1) = x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8)*x(i, 8);
x(i, 0) = x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8) * x(i, 8)*x(i, 8)*x(i, 8);
y(i, 0) = sin(x(i,8)*3.14);
sum = sum + 0.25;
cout << "w:" << endl;
cout << x << endl;
cout << "yt:" << endl;
cout << y.transpose() << endl;
w << 1, 1, 1, 1, 1, 1, 1, 1, 1, 1;
cout << "原始y_p:" << endl;
cout << (x * w).transpose() << endl;
MatrixXd y_p = x * w;
w = leastsq(y_p, y, x, w);
cout << "精确值" << endl;
cout << y.transpose() << endl;
cout << "变换后的y_p:" << endl;
cout << (x * w).transpose() << endl;
3 、总结
根据上诉公式，好像只需要变换一次，有点奇怪。实验证明，也只变了一次，误差就很小了。
以上是关于点云配准 -辅助知识 最小二乘法代码实现拟合曲线（C++）的主要内容，如果未能解决你的问题，请参考以下文章