数据结构：线性表顺序表以及单链表详解

Posted 2021-12-07 海是冰川蓝

导航🚀

• ⭐前言⭐
• 线性表
• • 线性表的定义及基本表示
  • • 线性表的定义
    • 基本操作
  • 顺序表
  • • 顺序表的定义
    • 顺序表的基本操作
    • • 增删查改
  • 线性表的链式表示
  • • 单链表的定义
    • 链表的建立
    • 链表的操作
    • • 插入节点
      • 删除结点

⭐前言⭐

本文将解析线性表中的顺序表以及链表

线性表

线性表的定义及基本表示

线性表的定义

线性表是具有相同数据类型的n个数据元素的有限集合。

常见的线性表有顺序表、链表、栈和队列。

基本操作

void InitList(&L);//初始化表。构造一个空的线性表。

int Length(L);//求表长。返回线性表L的长度，即L中数据元素的个数。

void LocateElem(L,e);//按值查找操作。在表L中查找具有给定关键字值的元素。

void GetElem(L,i);//按位查找操作。获取表L中第i个位置的元素的值。

void ListInsert(&L,i,e);//插入操作。在表L中的第i个位置上插入指定元素e。

void ListDelete(&L,i,&e);//删除操作。删除表L中第i个位置的元素，并用e返回删除元素的值

void PrintList(L);//输出操作。按前后顺序输出线性表L的所有元素值。

bool Empty(L);//判空操作。若L为空表，则返回true,否则返回false。

void DestroyList(&L);//销毁操作。销毁线性表，并释放线性表L所占用的内存空间。

顺序表

顺序表的定义

简而言之，数组。这就是说，顺序表的底层是通过数组来实现的。

静态数组版

//C语言实现
#define MaxSize 50//定义线性表最大长度
struct List{
    int data[MaxSize];//顺序表的元素，以int型数据为例
    int length;//顺序表当前长度，元素个数
}SqList;

动态数组版

//C语言实现
#define InitSize 100//表长度初始定义
struct List{
    int* data;//指示动态分配数组的指针
    int MaxSize,length;//数组最大容量和当前容量
}SeqList;
L.data=(int*)malloc(sizeof(int)*InitSize);
int* tmp=(int*)realloc(sizeof(int)*(MaxSize+10));
if(tmp){
    L.data=tmp;//判断扩容成功然后再改变指针指向
}

顺序表的基本操作

增删查改

下面以Java语言实现，与C语言不同的是Java可以在类的内部存放方法，便于操作。

建议先看前面的注释了解函数的作用，然后分析增删查改函数

//Java语言实现
public class MyArrayList {
    public int[] elem;
    public int usedSize;//有效的数据个数
    public MyArrayList() {
        this.elem = new int[10];
    }

    // 打印顺序表
    public void display() {
        for (int i = 0; i < this.usedSize; i++) {
            System.out.print(this.elem[i]+" ");
        }
        System.out.println();
    }

    // 获取顺序表的有效数据长度
    public int size() {
        return this.usedSize;
    }

    // 在 pos 位置新增元素，分析见后面
    public void add(int pos, int data) {
        if(pos<0||pos>this.usedSize){
            System.out.println("输入不合法");
            return;
        }
        if(isFull()){
            this.elem= Arrays.copyOf(this.elem,this.elem.length+10);
        }
        for(int i=this.usedSize-1;i>=pos;i--){
            elem[i+1]=elem[i];
        }
        elem[pos]=data;
        this.usedSize++;
    }
    //判断表是否满
    public boolean isFull() {
        return this.usedSize==this.elem.length;
    }
    //判断表是否为空
    public boolean isEmpty(){
        return this.usedSize==0;
    }

    // 判定是否包含某个元素
    public boolean contains(int toFind) {
        for (int x: elem) {
            if(x==toFind) return true;
        }
        return false;
    }
    // 查找某个元素对应的位置
    public int search(int toFind) {
        for (int i = 0; i < elem.length; i++) {
            if(elem[i]==toFind) return i;
        }
        return -1;
    }
    // 获取 pos 位置的元素
    public int getPos(int pos) {
        if(pos<0||pos>=this.usedSize){
            return -1;
        }
        if(isEmpty()){
            System.out.println("顺序表为空");
            return -1;
        }
        return elem[pos];
    }
    // 给 pos 位置的元素设为 value
    public void setPos(int pos, int value) {
        if(isEmpty()){
            System.out.println("顺序表为空");
            return;
        }
        if(pos<0||pos>=this.usedSize){
            System.out.println("输入不合法");
        }else{
            this.elem[pos]=value;
            System.out.println("设置成功");
        }
    }
    //删除第一次出现的关键字key
    public void remove(int toRemove) {
        if(isEmpty()){
            System.out.println("顺序表为空");
            return;
        }
        int pos=this.search(toRemove);
        if(pos==-1){
            System.out.println("删除元素不存在");
        }else{
            for(int i=pos;i<this.usedSize-1;i++){
                elem[i]=elem[i+1];
            }
            this.usedSize--;
            System.out.println("删除成功");
        }
    }
    // 清空顺序表
    public void clear() {
        this.usedSize=0;
        System.out.println("成功清空表");
    }
}

需要着重分析的是增加元素和删除元素

函数接口是void add(int pos,int data);

pos是插入位置，data是数值

首先判断pos的合法性，小于0不可以，大于使用长度也不可以

合法性判断后判断线性表是否满了，如果满了需要扩容，幸运的是，不用判断扩容的成功与失败。

比如我们要在pos为3的位置插入元素，我们就需要将pos以后的元素往后移动一位

如果插入pos为6呢？显然我们不需要移动元素了

那大于使用长度也不可以是什么意思？当我们插入pos=6时，pos等于usedSize的，当大于时，数组下标为6的空间没有被使用，这是不被允许的。

函数删除接口为void remove(int toRemove)

对表的删除首先要判断是不是空表，如果时空表我们就不能执行删除操作

然后找到删除元素的下标，如果不存在直接返回并提升不存在

如果存在,就需要后面的元素往前覆盖。

例如，我们要删除pos=2的元素，就要将后面的元素往前覆盖。

线性表的链式表示

单链表的定义

//C语言版
struct LNode{
    int data;//数据域，用一个整数来表示
    struct LNode *next;//指针域，指向下一个结点
};

下面给出链表的结构

下面给出单链表结构，双链表的结构以及循环单链表结构

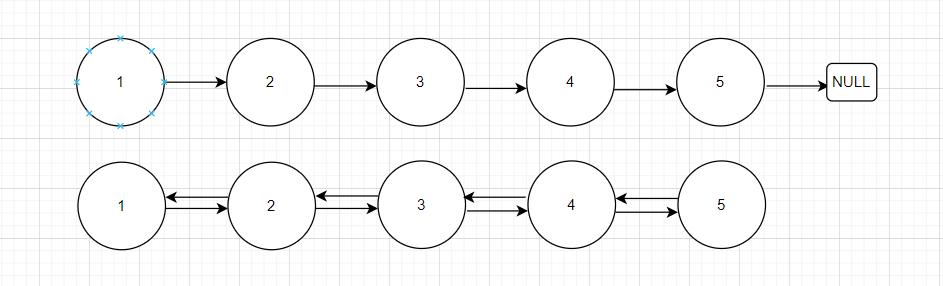
链表的建立

建立链表前需要初始化链表

//C语言版
//初始化链表
struct LNode* InitList(struct LNode* head){
    head=(struct LNode*)malloc(sizeof(LNode));
    head->next=NULL;
    return head;
}

头插法

顾名思义，就是再链表的头指针前插入元素

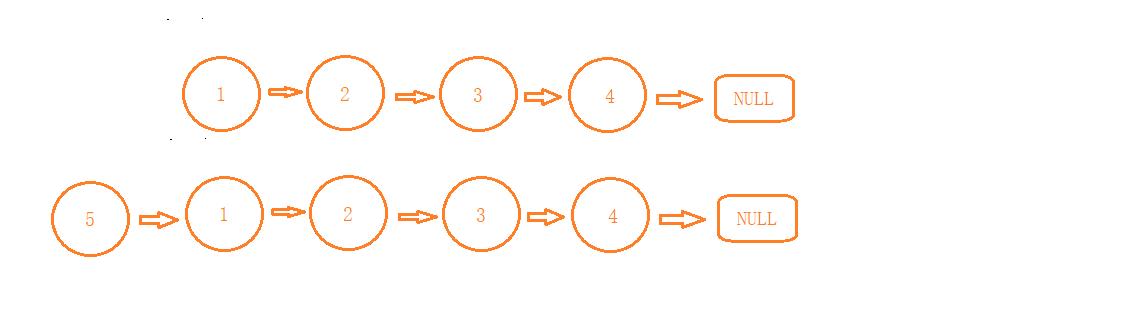
先前链表1->2->3->4->NULL
我们将5插入链表中
插入后5->1->2->3->4->NULL

struct LNode* headInsert(struct LNode* head) {
	struct LNode* p1=(struct LNode*)malloc(sizeof(LNode));
	printf("输入数据>");
	scanf("%d", &(p1->data));//结点的创建
	//核心操作
    p1->next = head;
	head = p1;
	return head;
}

尾插法

顾名思义，就是再链表的尾端插入

先前链表1->2->3->4->NULL
将5插入链表后1->2->3->4->5->NULL

需要注意的是，我们需要先前判断头指针是不是空指针。

struct LNode* tailInsert(struct LNode* head) {
    struct LNode* p2 = (LNode*)malloc(sizeof(LNode));
	printf("输入数据>");
	scanf("%d", &(p2->data));
    if(head==NULL){
        head=p2;
        return head;
    }
    //核心操作
	struct LNode* p1 = head;//p1用来帮助我们找到尾结点，p2用来插入
	while (p1->next) {
		p1 = p1->next;
	}
	p1->next = p2;
	p2->next = NULL;//尾结点后面没有了需要加NULL
	return head;
}

//上述尾插法室没有头结点的，如果有头结点，那要怎么插入
struct LNode* tailInsert(struct LNode* head){
    struct LNode*p1=(struct LNode*)malloc(sizeof(LNode));
    p1->next=head->next;
    head->next=p1;
    return head;
}
//@->1->2->3->NULL
//@->4->1->2->3->NULL

链表的操作

插入节点

void ListInsert(&L,i,e);

要想在第i个位置插入元素e，就要找到i-1的位置，假设第i-1个结点是p，然后将新结点q插入其后。

q->next=p->next;//步骤1
p->next=q;//步骤2

需要说明的是：当执行完步骤1时，1和3都指向2

如果步骤1和2反过来呢?

当我们p->next=q后，我们就丢失后面的结点

此时就是1->3->null连接

在很多境况我们采用的是尾插法，那要是插在头节点前呢？

可以使用头插法，也可以弄一个头节点来操作。

删除结点

删除结点需要找到前驱结点

假设p为前驱结点

q=p->next;
p->next=q->next;
free(q);

缺点是无法找到头节点的前驱结点

也可以将后面结点覆盖前面结点

假设p为被删除结点

q=p->next;
p->data=q->data;
p->next=q->next;
free(q);

需要注意的，第一个结点不能删除头结点，第二个方法不能删除尾结点。

第一个可以单独判头指针，但是尾指针判断较为困难

对于常规插入删除好像都不能顾全面，这时候可以在前面加一个哑结点，那样就不能考虑对头节点插入删除的困扰。