LeetCode 1824. 最少侧跳次数

Posted 2023-03-09 Tisfy

【LetMeFly】1824.最少侧跳次数

力扣题目链接：https://leetcode.cn/problems/minimum-sideway-jumps/

给你一个长度为 n 的 3 跑道道路 ，它总共包含 n + 1 个 点 ，编号为 0 到 n 。一只青蛙从 0 号点第二条跑道 出发 ，它想要跳到点 n 处。然而道路上可能有一些障碍。

给你一个长度为 n + 1 的数组 obstacles ，其中 obstacles[i] （取值范围从 0 到 3）表示在点 i 处的 obstacles[i] 跑道上有一个障碍。如果 obstacles[i] == 0 ，那么点 i 处没有障碍。任何一个点的三条跑道中 最多有一个 障碍。

• 比方说，如果 obstacles[2] == 1 ，那么说明在点 2 处跑道 1 有障碍。

这只青蛙从点 i 跳到点 i + 1 且跑道不变的前提是点 i + 1 的同一跑道上没有障碍。为了躲避障碍，这只青蛙也可以在 同一个 点处 侧跳 到 另外一条 跑道（这两条跑道可以不相邻），但前提是跳过去的跑道该点处没有障碍。

• 比方说，这只青蛙可以从点 3 处的跑道 3 跳到点 3 处的跑道 1 。

这只青蛙从点 0 处跑道 2 出发，并想到达点 n 处的 任一跑道 ，请你返回 最少侧跳次数 。

注意：点 0 处和点 n 处的任一跑道都不会有障碍。

 

示例 1：

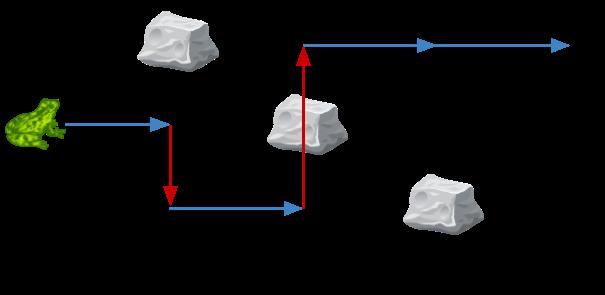
输入：obstacles = [0,1,2,3,0]
输出：2 
解释：最优方案如上图箭头所示。总共有 2 次侧跳（红色箭头）。
注意，这只青蛙只有当侧跳时才可以跳过障碍（如上图点 2 处所示）。

示例 2：

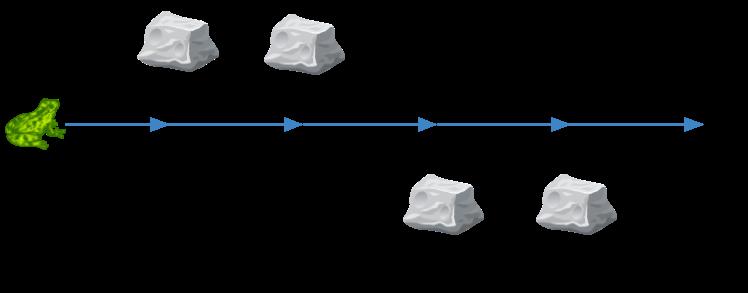
输入：obstacles = [0,1,1,3,3,0]
输出：0
解释：跑道 2 没有任何障碍，所以不需要任何侧跳。

示例 3：

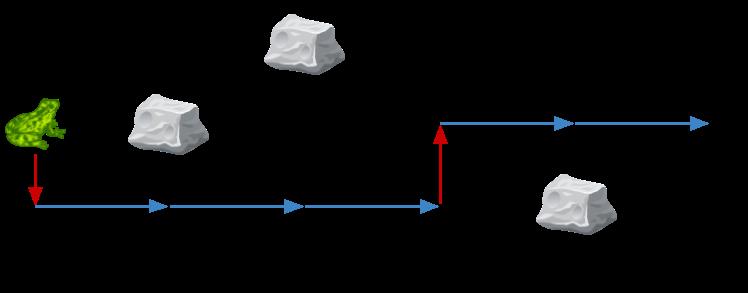
输入：obstacles = [0,2,1,0,3,0]
输出：2
解释：最优方案如上图所示。总共有 2 次侧跳。

 

提示：

• obstacles.length == n + 1
• 1 <= n <= 5 * 105
• 0 <= obstacles[i] <= 3
• obstacles[0] == obstacles[n] == 0

方法一：动态规划

也不用先像其他题解那样先考虑普通的DP再考虑如何原地滚动压缩优化到$O(1)$空间，直接考虑使用三个整型变量来当DP数组即可

dp[i]表示进行到当前距离时，若青蛙位于第i道上 的最小总横跳次数。

初始时青蛙的前进距离是0，并且位于中间的一道，因此初始值$dp[3]=1,0,1$

接着从起点的下一个位置遍历“障碍数组”，每次遍历时，我们分为两边：

1. 计算出到达这个前进距离所需的最小横跳次数
2. 更新三条跑道到这个前近距离的最小横跳次数

for (int i = 1; i < obstacles.size(); i++) 
	int minStep = 999999;
	// 计算出到达这个前进距离所需的最小横跳次数

	// 更新三条跑道到这个前近距离的最小横跳次数

最终，返回三条跑道的最小值即可。

• 时间复杂度$O(len(obstacles))$
• 空间复杂度$O(1)$

AC代码

C++

class Solution 
public:
    int minSideJumps(vector<int>& obstacles) 
        int dp[3] = 1, 0, 1;
        for (int i = 1; i < obstacles.size(); i++) 
            int minStep = 999999;
            for (int j = 0; j < 3; j++)   // 计算出到达这个前进距离所需的最小横跳次数
                if (obstacles[i] == j + 1)   // 若有障碍则不可达，记为“无穷大”
                    dp[j] = 999999;
                
                else 
                    minStep = min(minStep, dp[j]);
                
            
            for (int j = 0; j < 3; j++)   // 更新三条跑道到这个前近距离的最小横跳次数
                if (obstacles[i] != j + 1)   // 若此处非障碍，则可由此前进距离的另外两条跑道横跳而来
                    dp[j] = min(dp[j], minStep + 1);
                
            
        
        return min(dp[0], min(dp[1], dp[2]));
    
;

Python

class Solution:
    def minSideJumps(self, obstacles: List[int]) -> int:
        dp = [1, 0, 1]
        for i in range(1, len(obstacles)):
            minStep = 999999
            for j in range(3):
                if obstacles[i] == j + 1:
                    dp[j] = 999999
                else:
                    minStep = min(minStep, dp[j])
            for j in range(3):
                if obstacles[i] != j + 1:
                    dp[j] = min(dp[j], minStep + 1)
        return min(dp)

同步发文于CSDN，原创不易，转载请附上原文链接哦~
Tisfy：https://letmefly.blog.csdn.net/article/details/128745707