LeetCode 1824最少侧跳次数动态规划 HERODING的LeetCode之路

Posted 2023-02-13 HERODING23

解题思路：
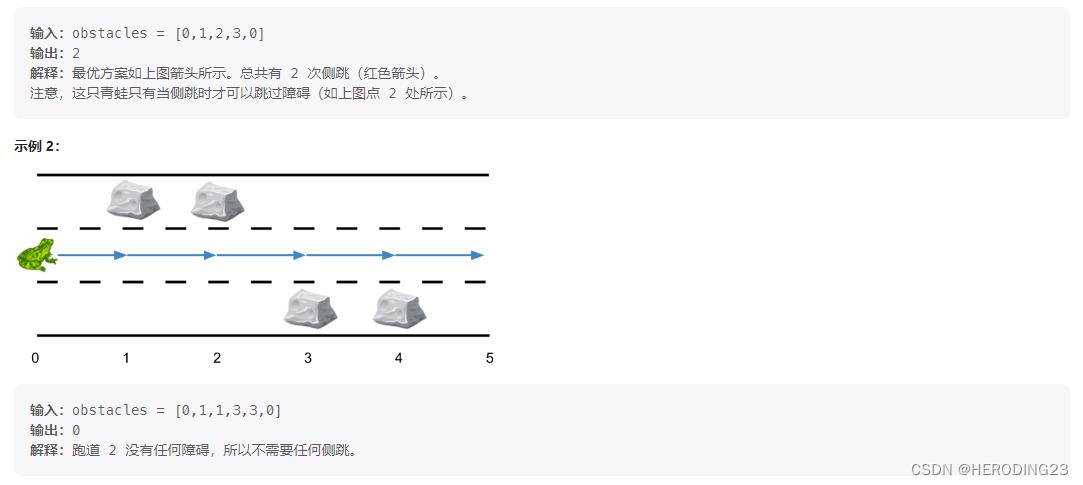
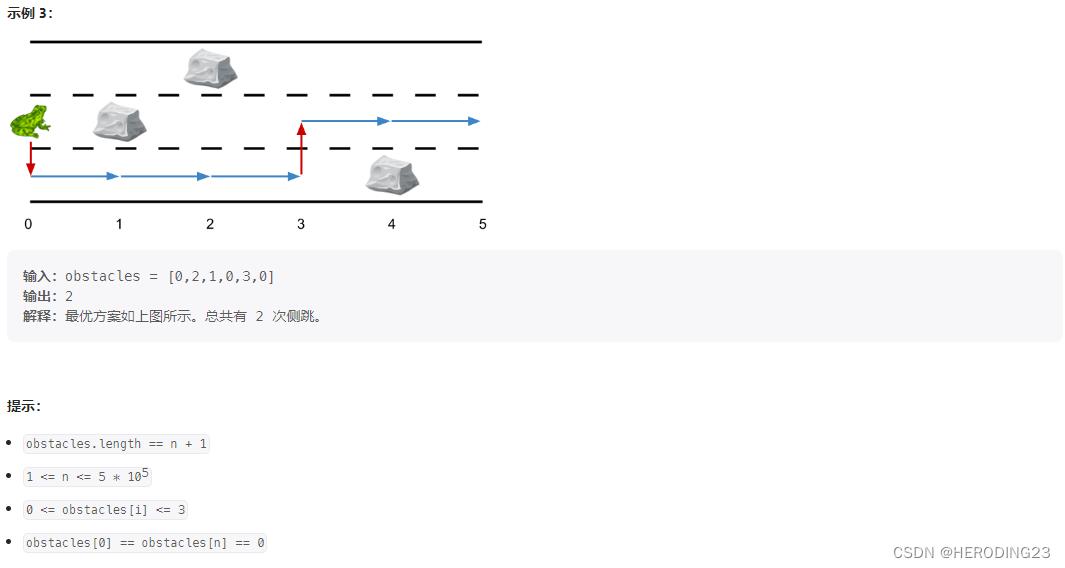
很有意思的一道动态规划题目，关键步骤是构建dp数组和状态转移方程，对于每个位置的青蛙，面对下一步有两种选择， 一种是继续前进，一种是跳到别的道路去，如果前面有石头就不能继续前进了，必须跳到别的道路上，这就有了我们的状态转移方程。dp数组定义为dp[i][j]，表示在i位置，处于道路j需要至少多少跳。面对第一种选择，如果没有石头，dp[i][j]=dp[i-1][j]即可，有石头更新为无穷大，同时更新当前最小跳数。接着就是第二种选择，是否跳到别的道路，实际上，应该是当前最优的位置是否跳到别的道路，即更新别的道路的最小跳数，最后返回最终列位置的最小跳数，步骤如下：

1. 定义dp数组，dp[0][0]和dp[0][2] 更新为1；
2. 遍历obstacles数组，处理第一种情况；
3. 处理第二种情况；
4. 返回最终列位置的最小跳数。

代码如下：

class Solution 
public:
    int minSideJumps(vector<int>& obstacles) 
        int n = obstacles.size();
        vector<vector<int>> dp(n + 1, vector<int>(3, 0));
        dp[0][0] = 1, dp[0][2] = 1;
        for(int i = 1; i <= n; i ++) 
            int minHop = INT_MAX;
            // 沿当前线路前进
            for(int j = 0; j < 3; j ++) 
                if(j == obstacles[i - 1] - 1) 
                    dp[i][j] = INT_MAX;
                 else 
                    dp[i][j] = dp[i - 1][j];
                    minHop = min(minHop, dp[i][j]);
                
            
            // 是否能够从最小跳数的路跳过来
            for(int j = 0; j < 3; j ++) 
                if(j == obstacles[i - 1] - 1) 
                    continue;
                 else 
                    dp[i][j] = min(dp[i][j], minHop + 1);
                
            
        
        return *min_element(dp[n].begin(), dp[n].end());
    
;

观察dp数组可以发现，只需要维护三个道路状态即可，即后一位置道路跳数只和上一位置道路跳数有关，代码如下：

class Solution 
public:
    int minSideJumps(vector<int>& obstacles) 
        vector<int> road = 1, 0 ,1;
        for(auto& obstacle : obstacles) 
            int minHop = INT_MAX;
            // 沿当前线路前进
            for(int i = 0; i < 3; i ++) 
                if(i == obstacle - 1) 
                    road[i] = INT_MAX;
                 else 
                    minHop = min(minHop, road[i]);
                
            
            // 是否能够跳到最小跳数的路
            for(int i = 0; i < 3; i ++) 
                if(i == obstacle - 1) 
                    continue;
                 else 
                    road[i] = min(road[i], minHop + 1);
                
            
        
        return *min_element(road.begin(), road.end());
    
;