Java 求解最长公共子序列&不相交的线&判断子序列&两个字符串的删除操作

Posted 2021-11-24 南淮北安

文章目录

• • 一、题目
  • 二、题解
  • 三、代码
  • 四、总结
  • 五、不相交的线
  • 六、判断子序列
  • 七、两个字符串的删除操作

一、题目

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如，“ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

二、题解

（1）确定 dp 数组以及下标含义

dp[i][j]：长度为 [0, i - 1] 的字符串 text1 与长度为 [0, j - 1] 的字符串 text2 的最长公共子序列为dp[i][j]

定义长度为 [0, i - 1] 的字符串 text1，是为了后续代码实现方便

（2）确定递推公式

主要就是两大情况：text1[i - 1] 与 text2[j - 1]相同，text1[i - 1] 与 text2[j - 1]不相同

如果text1[i - 1] 与 text2[j - 1] 相同，那么找到了一个公共元素，所以 dp[i][j] = dp[i - 1][j - 1] + 1;

如果text1[i - 1] 与 text2[j - 1] 不相同，那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列，取最大的。

既：dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1])

（3）确定 dp 数组初始化

dp[0][0]=0;

（4）确定遍历顺序

从递推公式，可以看出，有三个方向可以推出dp[i][j]，如图：

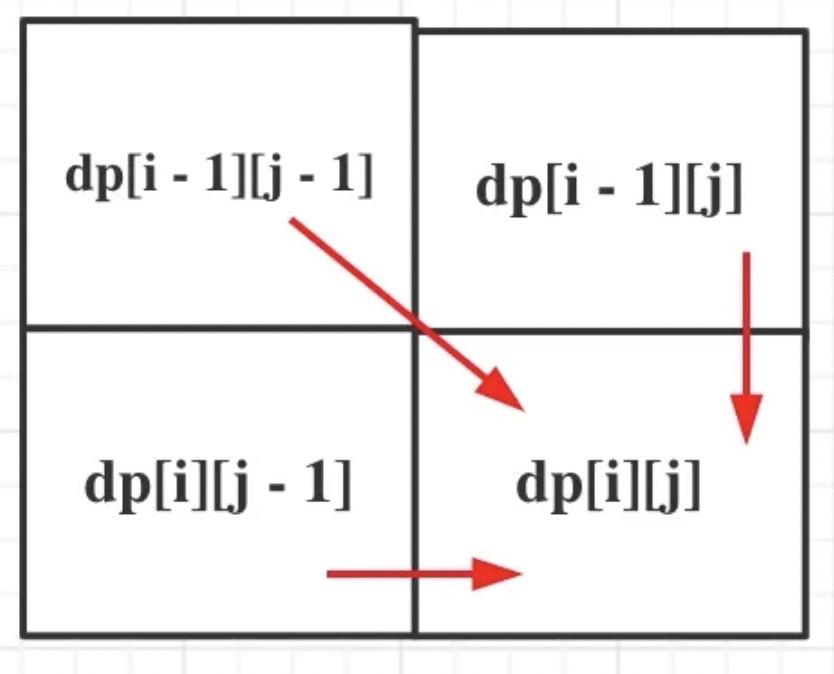
那么为了在递推的过程中，这三个方向都是经过计算的数值，所以要从前向后，从上到下来遍历这个矩阵。

三、代码

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int[][] dp = new int[text1.length() + 1][text2.length() + 1];
        dp[0][0] = 0;
        for (int i = 1; i <= text1.length(); i++) {
            for (int j = 1; j <= text2.length(); j++) {
                if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    // 如果当前位 i,j 不相等
                    // 取 Math.max(dp[i - 1][j], dp[i][j - 1])
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        // 由于不强调顺序，所以最后记录的就是最大值
        return dp[text1.length()][text2.length()];
    }
}

四、总结

该题只要求相对顺序不变，所以比较到最后一位记录的就是最大的长度

以前的题目，强调了相对顺序，所以需要遍历过程中需要记录最大长度

比如：2，5，1，7；

如果不强调顺序，递增的最大长度就是：2，5，7 为3

如果强调相对顺序就是 2，5

五、不相交的线

在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。

现在，可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，这些直线需要同时满足满足：

nums1[i] == nums2[j]

且绘制的直线不与任何其他连线（非水平线）相交。
请注意，连线即使在端点也不能相交：每个数字只能属于一条连线。

以这种方法绘制线条，并返回可以绘制的最大连线数。

该题和上面的求解类似，同样的方法就不再分析了

类似于两个数组，不强调顺序，求相同数字的最大个数

class Solution {
    public int maxUncrossedLines(int[] nums1, int[] nums2) {
        int[][] dp = new int[nums1.length+1][nums2.length+1];
        for(int i=1;i<=nums1.length;i++){
            for(int j=1;j<=nums2.length;j++){
                if(nums1[i-1]==nums2[j-1]){
                    dp[i][j] = dp[i-1][j-1]+1;
                }else{
                    dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);
                }
            }
        }
        return dp[nums1.length][nums2.length];
    }
}

六、判断子序列

给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。

该题和前两道题类似，可以采用同样的方法解题

不过，对于当 s.charAt(i-1)==t.charAt(j-1) 不成立时，dp[i][j]=dp[i][j-1]

意思是，当前j-1位不取

class Solution {
    public boolean isSubsequence(String s, String t) {
        if(s.length()==0){
            return true;
        }
        int[][] dp = new int[s.length()+1][t.length()+1];
        dp[0][0]=0;
        for(int i=1;i<=s.length();i++){
            for(int j=1;j<=t.length();j++){
                if(s.charAt(i-1)==t.charAt(j-1)){
                    dp[i][j]=dp[i-1][j-1]+1;
                }else{
                    dp[i][j]=dp[i][j-1];
                }
                if(dp[i][j]==s.length()){
                    return true;
                }
            }
        }
        return false;
    }
}

七、两个字符串的删除操作

给定两个单词 word1 和 word2，找到使得 word1 和 word2 相同所需的最小步数，每步可以删除任意一个字符串中的一个字符。

该题和上面的题目类似，可以理解为求两个字符串中最长的公共子序列（按顺序，不必连续）

找到最长的公共子序列之后，使两个字符串分别减去最长公共子序列的长度得到的值即是每个字符串需要删除的字符数目

class Solution {
    public int minDistance(String word1, String word2) {
        int[][] dp = new int[word1.length()+1][word2.length()+1];
        int res = 0; 
        for(int i=1;i<=word1.length();i++){
            for(int j=1;j<=word2.length();j++){
                if(word1.charAt(i-1)==word2.charAt(j-1)){
                    dp[i][j] = dp[i-1][j-1]+1;
                }else{
                    dp[i][j] = Math.max(dp[i][j-1],dp[i-1][j]);
                }
            }
        }
        res += word1.length()-dp[word1.length()][word2.length()];
        res += word2.length()-dp[word1.length()][word2.length()];
        return res;
    }
}