LeetCode（LCSி）最长公共子序列&变形应用

Posted 2021-10-15 白鳯

【LeetCode】（LCSி）最长公共子序列&变形应用

文章目录

• • 【LeetCode】（LCSி）最长公共子序列&变形应用
  • • 最长公共子序列★★
    • 不相交的线★★
    • 最长回文子序列★★
    • 两个字符串的删除操作★★

最长公共子序列★★

1143. 最长公共子序列

【题目】

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如，"ace" 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列

提示：

• 1 <= text1.length, text2.length <= 1000
• text1 和 text2 仅由小写英文字符组成。

【示例】

输入：text1 = "abcde", text2 = "ace" 
输出：3  
解释：最长公共子序列是 "ace" ，它的长度为 3 。
------------------------------------------
输入：text1 = "abc", text2 = "abc"
输出：3
解释：最长公共子序列是 "abc" ，它的长度为 3 。
------------------------------------------
输入：text1 = "abc", text2 = "def"
输出：0
解释：两个字符串没有公共子序列，返回 0 。

【解题思路】

dp[i][j]的含义是text1[0...i]与text2[0...j]的最长公共子序列的长度。从左到右，从上到下计算矩阵dp

其状态转移如下：
$$dp[i][j]=\{\begin{array}{l}dp[i-1][j-1]+1,iftext1[i]=text[j]\\ max(dp[i-1][j],dp[i][j-1]),iftext1[i]\ne text[j]\end{array}$$
详细过程如下图所示

其代码实现如下：

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int n1 = text1.length(), n2 = text2.length();
        int[][] dp = new int[n1 + 1][n2 + 2];
        for (int i = 0; i < n1; i++) {
            for (int j = 0; j < n2; j++) {
                if (text1.charAt(i) == text2.charAt(j)) {
                    dp[i + 1][j + 1] = dp[i][j] + 1;
                } else {
                    dp[i + 1][j + 1] = Math.max(dp[i + 1][j], dp[i][j + 1]);
                }
            }
        }
        return dp[n1][n2];
    }
}

---

不相交的线★★

1035. 不相交的线

【题目】

在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。

现在，可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，这些直线需要同时满足满足：

nums1[i] == nums2[j]
且绘制的直线不与任何其他连线（非水平线）相交。
请注意，连线即使在端点也不能相交：每个数字只能属于一条连线。

以这种方法绘制线条，并返回可以绘制的最大连线数。

【示例】

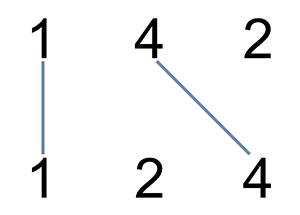
输入：nums1 = [1,4,2], nums2 = [1,2,4]
输出：2
解释：可以画出两条不交叉的线，如上图所示。 
但无法画出第三条不相交的直线，因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。
----------------------------------------------------------------------
输入：nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2]
输出：3

【解题思路】

显然，这就是一道最长公共子序列的问题，只不过换了个说法而已

class Solution {
    public int maxUncrossedLines(int[] nums1, int[] nums2) {
        int m = nums1.length, n = nums2.length;
        int[][] dp = new int[m + 1][n + 1];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (nums1[i] == nums2[j]) {
                    dp[i + 1][j + 1] = dp[i][j] + 1;
                } else {
                    dp[i + 1][j + 1] = Math.max(dp[i + 1][j], dp[i][j + 1]);
                }
            }
        }
        return dp[m][n];
    }
}

---

最长回文子序列★★

516. 最长回文子序列

【题目】

给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度。

子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。

提示：

• 1 <= s.length <= 1000
• s 仅由小写英文字母组成

【示例】

输入：s = "bbbab"
输出：4
解释：一个可能的最长回文子序列为 "bbbb" 。
---------------------------------------
输入：s = "cbbd"
输出：2
解释：一个可能的最长回文子序列为 "bb" 。

【解题思路】

可转化为求原字符串与其逆序字符串的最长公共子序列问题

class Solution {
    public int longestPalindromeSubseq(String s) {
        int n = s.length();
        int[][] dp = new int[n + 1][n + 1];
        //最长公共子序列
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                char a = s.charAt(i);
                char b = s.charAt(n - j - 1);
                if (a == b) {
                    dp[i + 1][j + 1] = dp[i][j] + 1;
                } else {
                    dp[i + 1][j + 1] = Math.max(dp[i + 1][j], dp[i][j + 1]);
                }
            }
        }
        return dp[n][n];
    }
}

---

两个字符串的删除操作★★

583. 两个字符串的删除操作

【题目】

给定两个单词 word1 和 word2，找到使得 word1 和 word2 相同所需的最小步数，每步可以删除任意一个字符串中的一个字符。

提示：

1. 给定单词的长度不超过500。
2. 给定单词中的字符只含有小写字母。

【示例】

输入: "sea", "eat"
输出: 2
解释: 第一步将"sea"变为"ea"，第二步将"eat"变为"ea"

【解题思路】

可先求得其最长的公共子序列，剩余的字符个数就是其需要删除的最少次数

class Solution {
    public int minDistance(String word1, String word2) {
        int m = word1.length(), n = word2.length();
        int[][] dp = new int[m + 1][n + 1];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (word1.charAt(i) == word2.charAt(j)) {
                    dp[i + 1][j + 1] = dp[i][j] + 1;
                } else {
                    dp[i + 1][j + 1] = Math.max(dp[i + 1][j], dp[i][j + 1]);
                }
            }
        }
        return m + n - dp[m][n] * 2;
    }
}