数据结构与算法之深入解析N个数全排列的求解思路与算法示例

Posted 2021-11-23 Forever_wj

一、全排列 I

① 题目描述

• 给定一个不含重复数字，长度为 N 的数组 nums ，返回其所有可能的全排列，可以按任意顺序返回结果。
• 示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

• 示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]

• 示例 3：

输入：nums = [1]
输出：[[1]]

② 算法分析

• 采用分治法把大问题分解成很多的子问题。大问题是所有的排列方法，分解得到的小问题就是以 1 开头的排列，以 2 开头的排列，以 a 开头的排列，以 b 开头的排列…把这些问题继续分解，以 12 开头的排列，以 123 开头的排列…将余下的看成大问题，一直分解下去，直到分解成的子问题只有一个数字或字符的时候，不再分解。
• 因为 1 个数字或字符肯定只有一种排列方式，现在将每个解决了的小问题合并，合并成一个大点的问题，合并之后这个大点的问题也解决了，再将这些大点的问题合并成一个更大的问题，直到最大的问题解决为止。
• 先固定一个字符，然后将固定的字符与它后面的每一个进行交换，一直递归下去，直到固定的字符后面只有一个字符。
• 如下图所示，红色字符是被固定的字符，白色字符的没有被固定的字符，具体做法就是每次将没有固定的第一个字符与其他未固定的字符交换（第 1 个与第 1个交换，第 1 个与第 2 个交换，… 第 1 个与第 n 个交换），直到只剩下一个没有被固定的字符时，输出此时的字符排列，但是输出之后要将字符的位置还原。

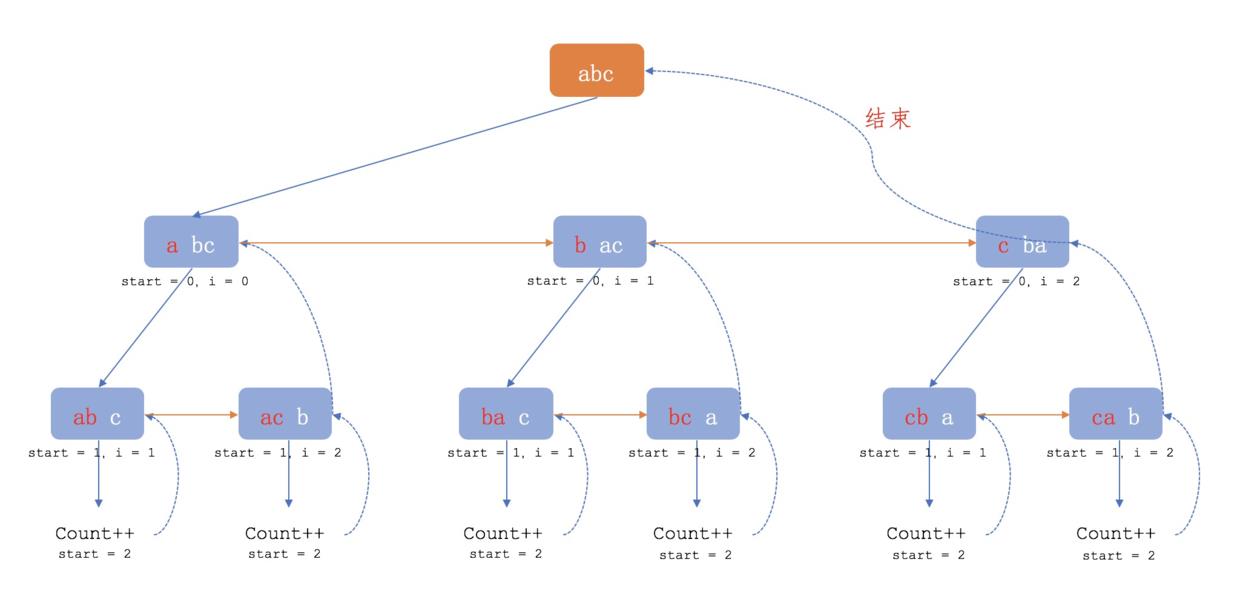
• 全排列可以看做固定前 i 位，对第 i+1 位之后的再进行全排列，比如固定第一位，后面跟着 n-1 位的全排列，那么解决 n-1 位元素的全排列就能解决 n 位元素的全排列。

③ C 算法示例

#include <stdio.h>
#include <string.h>

char temp;
void swapChar(char a[], int i, int k) {
    temp = a[i];
    a[i] = a[k];
    a[k] = temp;
}

void algorithm(char a[], int start, unsigned long count) {
    // 深度控制。此时只剩一个没有固定的字符，直接输出
    if(start == count - 1) {
        puts(a);   return;
    }
    
    for(int i = start; i < count; i++) {
        
        swapChar(a, i, start);  // 交换
        
        algorithm(a, start + 1, count);
        
        swapChar(a, i, start);  // 复原
    }
}

int main() {
    char arr[100] = { 'a', 'b', 'c' };  // gets(a);
    
    algorithm(arr, 0, strlen(arr));
    
    return 0;
}

二、全排列 II

① 题目描述

• 给定一个可包含重复数字的序列 nums ，按任意顺序返回所有不重复的全排列。
• 示例 1：

输入：nums = [1,1,2]
输出：
[[1,1,2],
 [1,2,1],
 [2,1,1]]

• 示例 2：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

② 思路分析

• 这个题目可以看作有 n 个排列成一行的空格，我们需要从左往右依次填入题目给定的 n 个数，每个数只能使用一次，那么很直接的可以想到一种穷举的算法，即从左往右每一个位置都依此尝试填入一个数，看能不能填完这 n 个空格，在程序中可以用“回溯法”来模拟这个过程。
• 定义递归函数 backtrack(idx, perm) 表示当前排列为 perm，下一个待填入的位置是第 idx 个位置（下标从 0 开始），那么整个递归函数分为两个情况：
• • 如果 idx==n，说明已经填完 n 个位置，找到了一个可行的解，将 perm 放入答案数组中，递归结束。
• • 如果 idx<n，我们要考虑第 idx 个位置填哪个数。根据题目要求，我们肯定不能填已经填过的数，因此很容易想到的一个处理手段是我们定义一个标记数组 vis 来标记已经填过的数，那么在填第 idx 个数的时候我们遍历题目给定的 n 个数，如果这个数没有被标记过，我们就尝试填入，并将其标记，继续尝试填下一个位置，即调用函数 backtrack(idx + 1, perm)。搜索回溯的时候要撤销该个位置填的数以及标记，并继续尝试其他没被标记过的数。
• 但题目解到这里并没有满足「全排列不重复」 的要求，在上述的递归函数中我们会生成大量重复的排列，因为对于第 idx 的位置，如果存在重复的数字 i，我们每次会将重复的数字都重新填上去并继续尝试导致最后答案的重复，因此我们需要处理这个情况。
• 要解决重复问题，我们只要设定一个规则，保证在填第 idx 个数的时候重复数字只会被填入一次即可。而在本题解中，我们选择对原数组排序，保证相同的数字都相邻，然后每次填入的数一定是这个数所在重复数集合中「从左往右第一个未被填过的数字」，即如下的判断条件：

if (i > 0 && nums[i] == nums[i - 1] && !vis[i - 1]) {
    continue;
}

• 这个判断条件保证了对于重复数的集合，一定是从左往右逐个填入的。
• 假设有 3 个重复数排完序后相邻，那么一定保证每次都是拿从左往右第一个未被填过的数字，即整个数组的状态其实是保证了 [未填入，未填入，未填入] 到 [填入，未填入，未填入]，再到 [填入，填入，未填入]，最后到 [填入，填入，填入] 的过程的，因此可以达到去重的目标。

③ C 算法示例

int* vis;

void backtrack(int* nums, int numSize, int** ans, int* ansSize, int idx, int* perm) {
    if (idx == numSize) {
        int* tmp = malloc(sizeof(int) * numSize);
        memcpy(tmp, perm, sizeof(int) * numSize);
        ans[(*ansSize)++] = tmp;
        return;
    }
    for (int i = 0; i < numSize; ++i) {
        if (vis[i] || (i > 0 && nums[i] == nums[i - 1] && !vis[i - 1])) {
            continue;
        }
        perm[idx] = nums[i];
        vis[i] = 1;
        backtrack(nums, numSize, ans, ansSize, idx + 1, perm);
        vis[i] = 0;
    }
}

int cmp(void* a, void* b) {
    return *(int*)a - *(int*)b;
}

int** permuteUnique(int* nums, int numsSize, int* returnSize, int** returnColumnSizes) {
    int** ans = malloc(sizeof(int*) * 2001);
    int* perm = malloc(sizeof(int) * 2001);
    vis = malloc(sizeof(int) * numsSize);
    memset(vis, 0, sizeof(int) * numsSize);
    qsort(nums, numsSize, sizeof(int), cmp);
    *returnSize = 0;
    backtrack(nums, numsSize, ans, returnSize, 0, perm);
    *returnColumnSizes = malloc(sizeof(int) * (*returnSize));
    for (int i = 0; i < *returnSize; i++) {
        (*returnColumnSizes)[i] = numsSize;
    }
    return ans;
}

• 时间复杂度：O(n×n!)，其中 n 为序列的长度。
• 空间复杂度：O(n)。