数据结构与算法之深入解析“下一个排列”的求解思路与算法示例

Posted 2022-02-12 Serendipity·y

一、题目要求

• 整数数组的一个排列，就是将其所有成员以序列或线性顺序排列。
• 例如，arr = [1,2,3] ，以下这些都可以视作 arr 的排列：[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。
• 整数数组的下一个排列是指其整数的下一个字典序更大的排列。更正式地，如果数组的所有排列根据其字典顺序从小到大排列在一个容器中，那么数组的下一个排列就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列，那么这个数组必须重排为字典序最小的排列（即，其元素按升序排列）。
• • 例如，arr = [1,2,3] 的下一个排列是 [1,3,2] 。
• • 类似地，arr = [2,3,1] 的下一个排列是 [3,1,2] 。
• • 而 arr = [3,2,1] 的下一个排列是 [1,2,3]，因为 [3,2,1] 不存在一个字典序更大的排列。
• 给你一个整数数组 nums ，找出 nums 的下一个排列。
• 必须原地修改，只允许使用额外常数空间。
• 示例 1：

输入：nums = [1,2,3]
输出：[1,3,2]

• 示例 2：

输入：nums = [3,2,1]
输出：[1,2,3]

• 示例 3：

输入：nums = [1,1,5]
输出：[1,5,1]

• 提示：
• • 1 <= nums.length <= 100
• • 0 <= nums[i] <= 100

二、思路分析

• “下一个排列”的定义是：给定数字序列的字典序中下一个更大的排列。如果不存在下一个更大的排列，则将数字重新排列成最小的排列（即升序排列）。我们可以将该问题形式化地描述为：给定若干个数字，将其组合为一个整数。如何将这些数字重新排列，以得到下一个更大的整数如果没有更大的整数，则输出最小的整数。
• 题目要求实现一个算法，将给定数字序列重新排列成字典序中下一个更大的排列。以数字序列 [1,2,3] 为例，其排列按照字典序依次为：[1,2,3]、[1,3,2]、[2,1,3]、[2,3,1]、[3,1,2]、[3,2,1]，这样，排列 [2,3,1] 的下一个排列即为 [3,1,2]。特别的，最大的排列 [3,2,1] 的下一个排列为最小的排列 [1,2,3]。那么，如何得到这样的排列顺序呢？
• • 我们希望下一个数比当前数大，这样才满足“下一个排列”的定义。因此只需要将后面的「大数」与前面的「小数」交换，就能得到一个更大的数。比如 123456，将 5 和 6 交换就能得到一个更大的数 123465。
• • 还希望下一个数增加的幅度尽可能的小，这样才满足“下一个排列与当前排列紧邻“的要求，为了满足这个要求，就需要：
• • • 在尽可能靠右的低位进行交换，需要从后向前查找；
• • • 将一个 尽可能小的「大数」 与前面的「小数」交换。比如 123465，下一个排列应该把 5 和 4 交换而不是把 6 和 4 交换；
• • • 将「大数」换到前面后，需要将「大数」后面的所有数重置为升序，升序排列就是最小的排列。以 123465 为例：首先按照上一步，交换 5 和 4，得到 123564；然后需要将 5 之后的数重置为升序，得到 123546。显然 123546 比 123564 更小，123546 就是 123465 的下一个排列。

三、求解算法

① 两遍扫描

• 注意到下一个排列总是比当前排列要大，除非该排列已经是最大的排列。我们希望找到一种方法，能够找到一个大于当前序列的新序列，且变大的幅度尽可能小。具体地：
• • 需要将一个左边的「较小数」与一个右边的「较大数」交换，以能够让当前排列变大，从而得到下一个排列。
• • 同时要让这个「较小数」尽量靠右，而「较大数」尽可能小。当交换完成后，「较大数」右边的数需要按照升序重新排列。这样可以在保证新排列大于原来排列的情况下，使变大的幅度尽可能小。
• 以排列 [4,5,2,6,3,1] 为例：
• • 能找到的符合条件的一对「较小数」与「较大数」的组合为 2 与 3，满足「较小数」尽量靠右，而「较大数」尽可能小。
• • 当完成交换后排列变为 [4,5,3,6,2,1]，此时可以重排「较小数」右边的序列，序列变为 [4,5,3,1,2,6]。
• 具体地，这样描述该算法，对于长度为 n 的排列 a：
• • 首先从后向前查找第一个顺序对 (i,i+1)，满足 a[i]<a[i+1]。这样「较小数」即为 a[i]。此时 [i+1,n) 必然是下降序列。
• • 如果找到了顺序对，那么在区间 [i+1,n) 中从后向前查找第一个元素 j 满足 a[i]<a[j]。这样「较大数」即为 a[j]。
• • 交换 a[i] 与 a[j]，此时可以证明区间 [i+1,n) 必为降序，可以直接使用双指针反转区间 [i+1,n) 使其变为升序，而无需对该区间进行排序。

• C++ 示例：

class Solution 
public:
    void nextPermutation(vector<int>& nums) 
        int i = nums.size() - 2;
        while (i >= 0 && nums[i] >= nums[i + 1]) 
            i--;
        
        if (i >= 0) 
            int j = nums.size() - 1;
            while (j >= 0 && nums[i] >= nums[j]) 
                j--;
            
            swap(nums[i], nums[j]);
        
        reverse(nums.begin() + i + 1, nums.end());
    
;

• Java 示例：

class Solution 
    public void nextPermutation(int[] nums) 
        int i = nums.length - 2;
        while (i >= 0 && nums[i] >= nums[i + 1]) 
            i--;
        
        if (i >= 0) 
            int j = nums.length - 1;
            while (j >= 0 && nums[i] >= nums[j]) 
                j--;
            
            swap(nums, i, j);
        
        reverse(nums, i + 1);
    

    public void swap(int[] nums, int i, int j) 
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    

    public void reverse(int[] nums, int start) 
        int left = start, right = nums.length - 1;
        while (left < right) 
            swap(nums, left, right);
            left++;
            right--;
        
    

② 标准的“下一个排列”算法

• 标准的“下一个排列”算法可以描述为：
• • 从后向前查找第一个相邻升序的元素对 (i,j)，满足 A[i] < A[j]，此时 [j,end) 必然是降序；
• • 在 [j,end) 从后向前查找第一个满足 A[i] < A[k] 的 k，A[i]、A[k] 分别就是上文所说的「小数」、「大数」；
• • 将 A[i] 与 A[k] 交换；
• • 可以断定这时 [j,end) 必然是降序，逆置 [j,end)，使其升序；
• • 如果在步第一步找不到符合的相邻元素对，说明当前 [begin,end) 为一个降序顺序，则直接跳到第四步。
• 以求 12385764 的下一个排列为例：

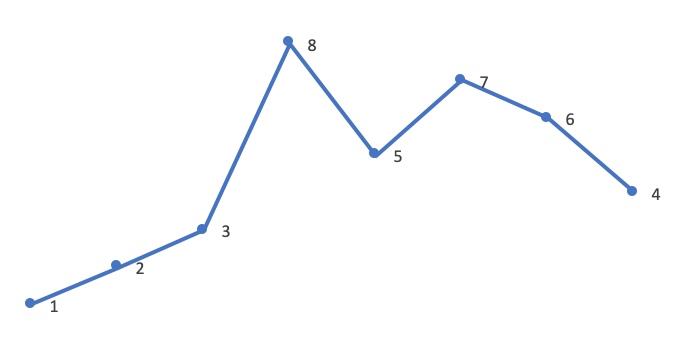
• 首先从后向前查找第一个相邻升序的元素对 (i,j)，这里 i=4，j=5，对应的值为 5，7：

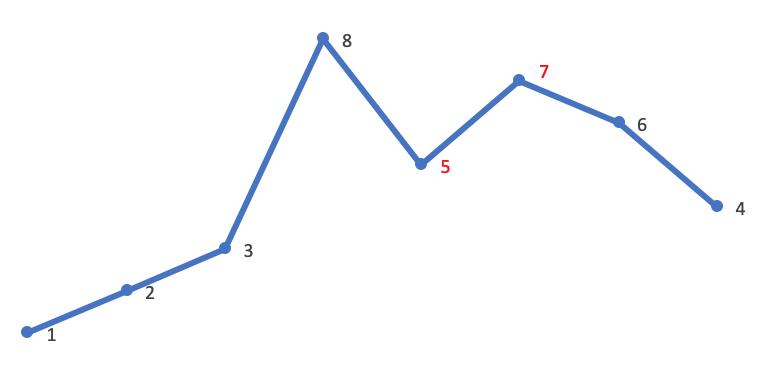
• 然后在 [j,end) 从后向前查找第一个大于 A[i] 的值 A[k]，这里 A[i] 是 5，故 A[k] 是 6：

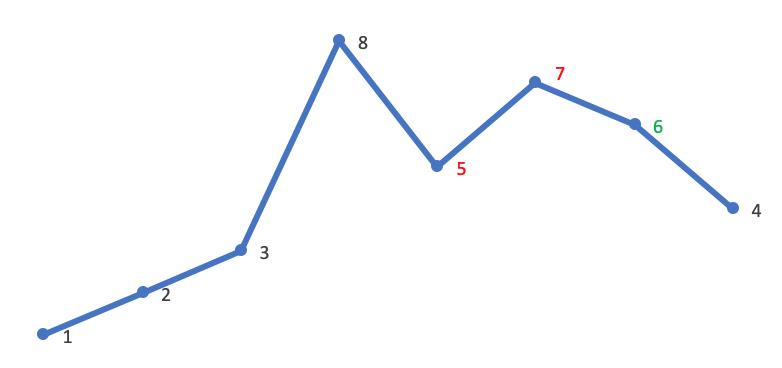
• 将 A[i] 与 A[k] 交换，这里交换 5、6：

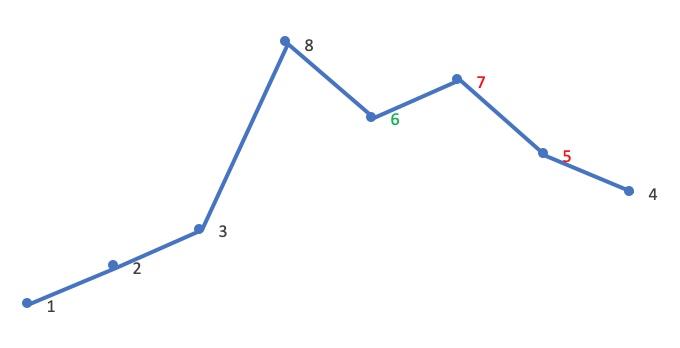
• 这时 [j,end) 必然是降序，逆置 [j,end)，使其升序，这里逆置 [7,5,4]：

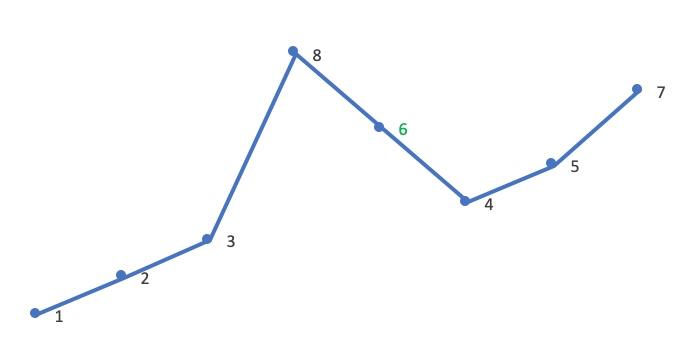
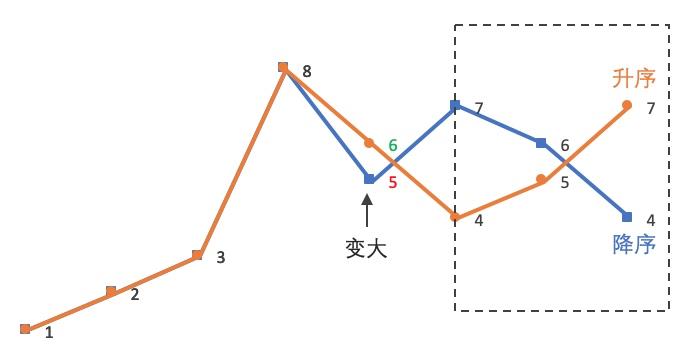
• 因此，12385764 的下一个排列就是 12386457。最后再对比一下这两个相邻的排列（橙色是蓝色的下一个排列）：

• 示例：

class Solution 
    public void nextPermutation(int[] nums) 
        int len = nums.length;
        for (int i = len - 1; i > 0; i--) 
                if (nums[i] > nums[i - 1]) 
                    Arrays.sort(nums, i, len);
                    for (int j = i; j <len; j++) 
                        if (nums[j] > nums[i - 1]) 
                            int temp = nums[j];
                            nums[j] = nums[i - 1];
                            nums[i - 1] = temp;
                            return;
                        
                    
                
            
    	Arrays.sort(nums);
		return;  
    
 

func nextPermutation(nums []int) 
	if len(nums) <= 1 
		return
	

	i, j, k := len(nums)-2, len(nums)-1, len(nums)-1

	// find: A[i]<A[j]
	for i >= 0 && nums[i] >= nums[j] 
		i--
		j--
	

	if i >= 0  // 不是最后一个排列
		// find: A[i]<A[k]
		for nums[i] >= nums[k] 
			k--
		
		// swap A[i], A[k]
		nums[i], nums[k] = nums[k], nums[i]
	

	// reverse A[j:end]
	for i, j := j, len(nums)-1; i < j; i, j = i+1, j-1 
		nums[i], nums[j] = nums[j], nums[i]