数据结构与算法之深入解析“排列序列”的求解思路与算法示例

Posted 2022-02-18 Serendipity·y

一、题目要求

• 给出集合 [1,2,3,…,n]，其所有元素共有 n! 种排列。
• 按大小顺序列出所有排列情况，并一一标记，当 n = 3 时, 所有排列如下：
• • “123”
• • “132”
• • “213”
• • “231”
• • “312”
• • “321”
• 给定 n 和 k，返回第 k 个排列。
• 示例 1：

输入：n = 3, k = 3
输出："213"

• 示例 2：

输入：n = 4, k = 9
输出："2314"

• 示例 3：

输入：n = 3, k = 1
输出："123"

• 提示：
• • 1 <= n <= 9
• • 1 <= k <= n!

二、求解算法

① 深度优先遍历 + 剪枝

• 容易想到，使用同“全排列”的回溯搜索算法，依次得到全排列，输出第 k 个全排列即可，具体可参考：【数据结构与算法】之深入解析N个数全排列的求解思路与算法示例。事实上，我们不必求出所有的全排列。
• 所求排列 一定在叶子结点处得到，进入每一个分支，可以根据已经选定的数的个数，进而计算还未选定的数的个数，然后计算阶乘，就知道这一个分支的 叶子结点 的个数：
• • 如果 k 大于这一个分支将要产生的叶子结点数，直接跳过这个分支，这个操作叫「剪枝」；
• • 如果 k 小于等于这一个分支将要产生的叶子结点数，那说明所求的全排列一定在这一个分支将要产生的叶子结点里，需要递归求解。

• 以示例 2：输入: n=4，k=9，使用「回溯 + 剪枝」的思想得到输出 “2314”：

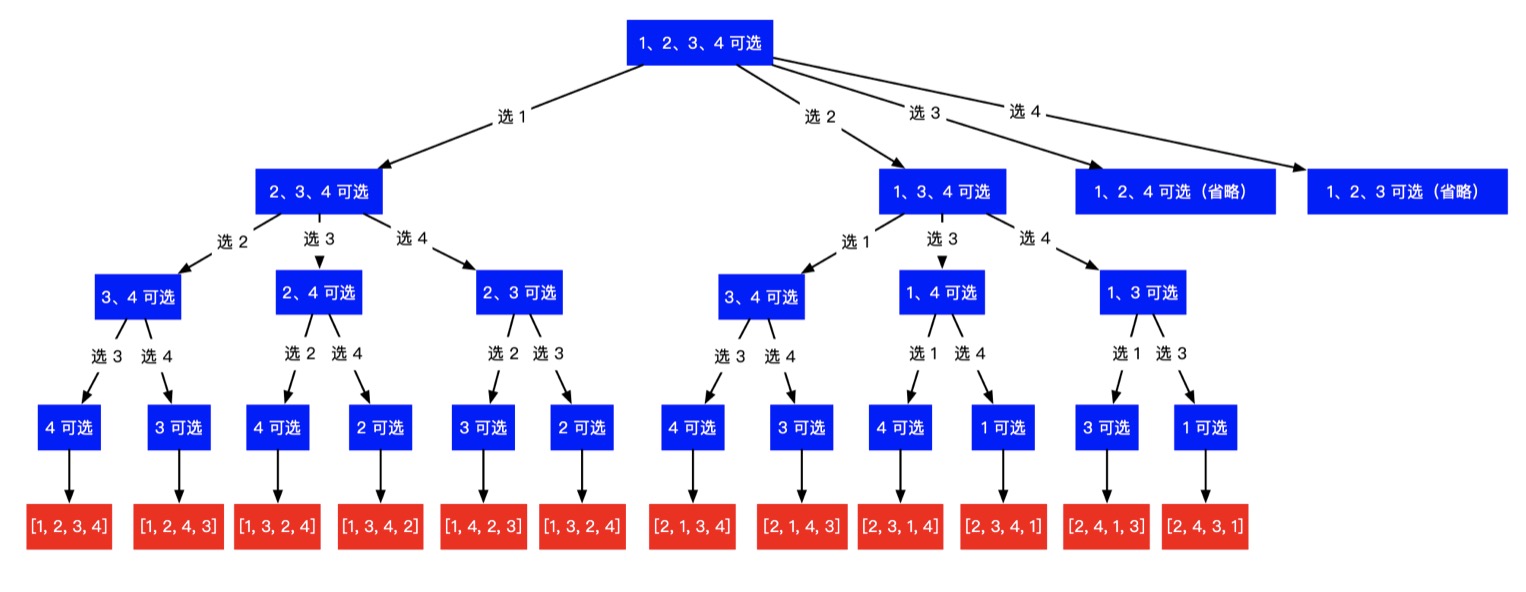
• 所求排列一定在叶子结点处得到：

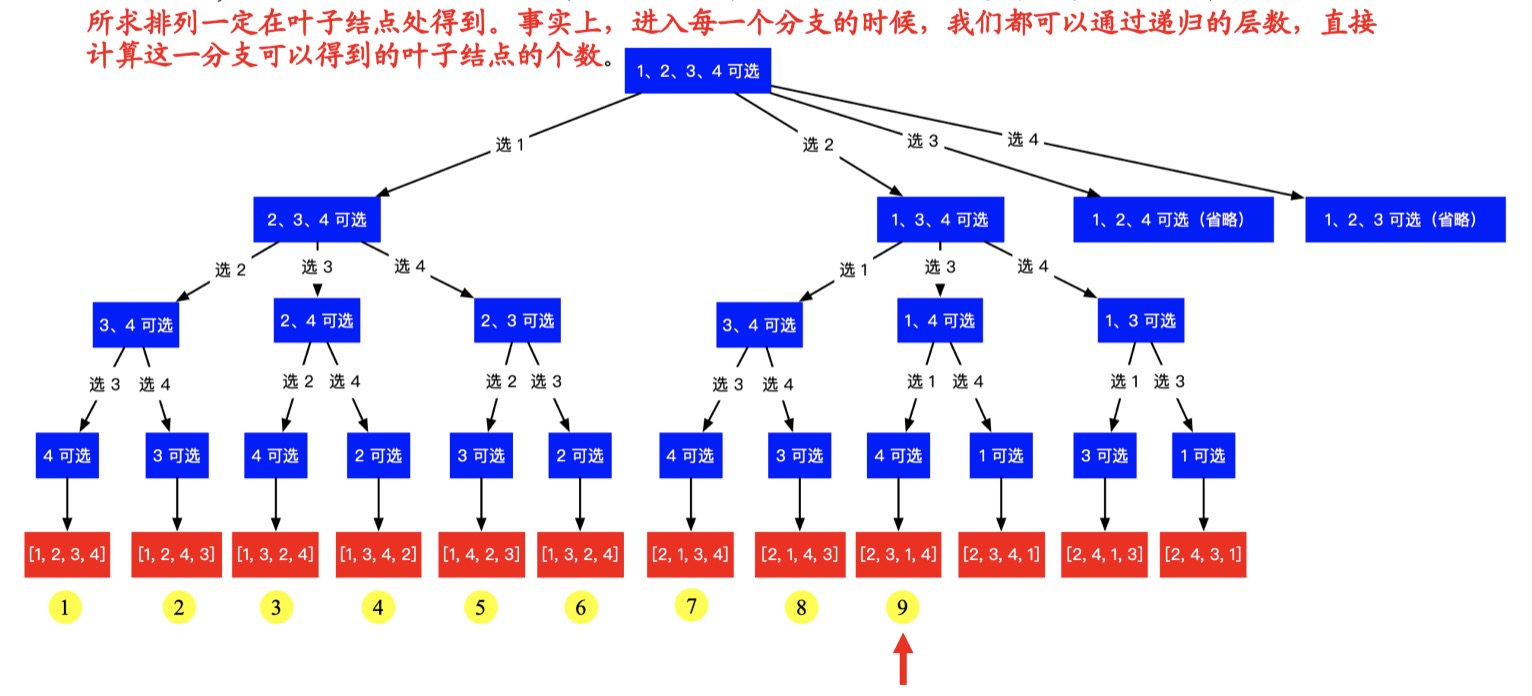
• 第一层，以 1 开头：

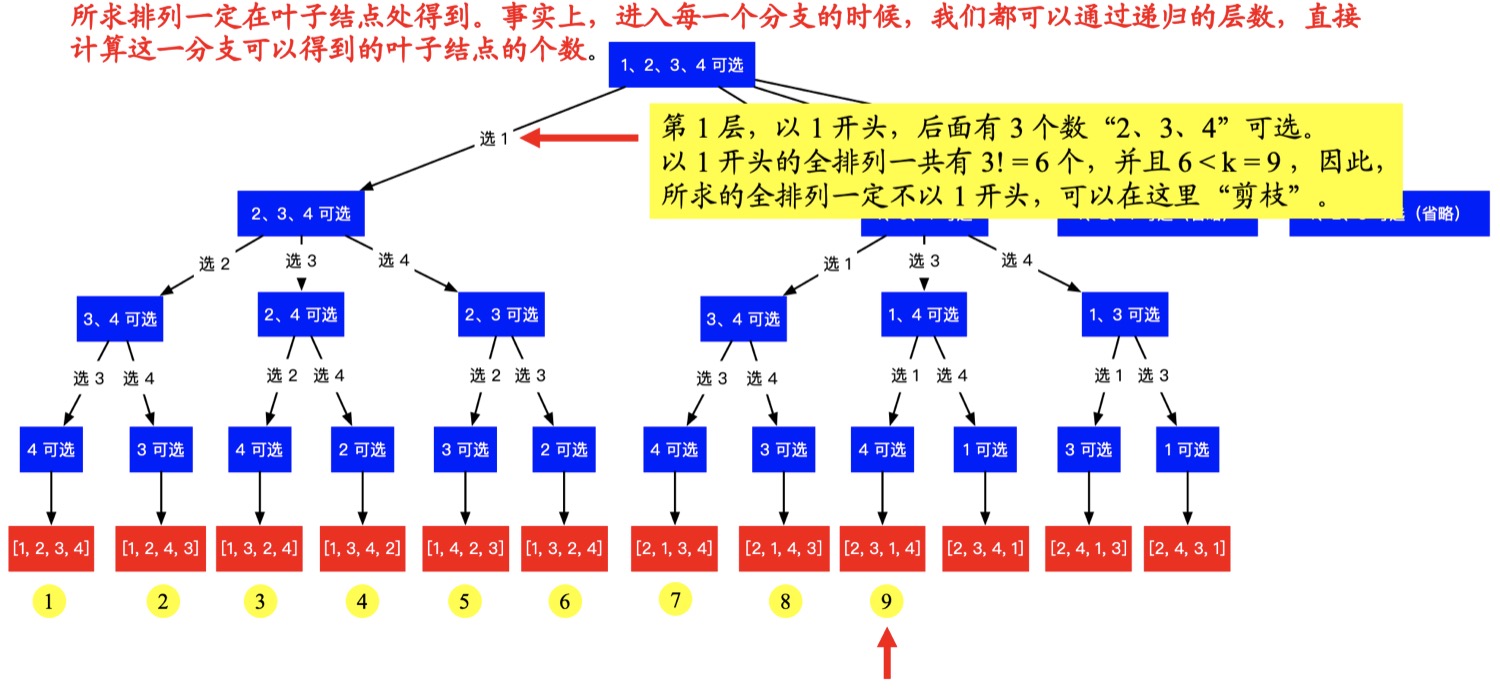
• 第一层，以 2 开头：

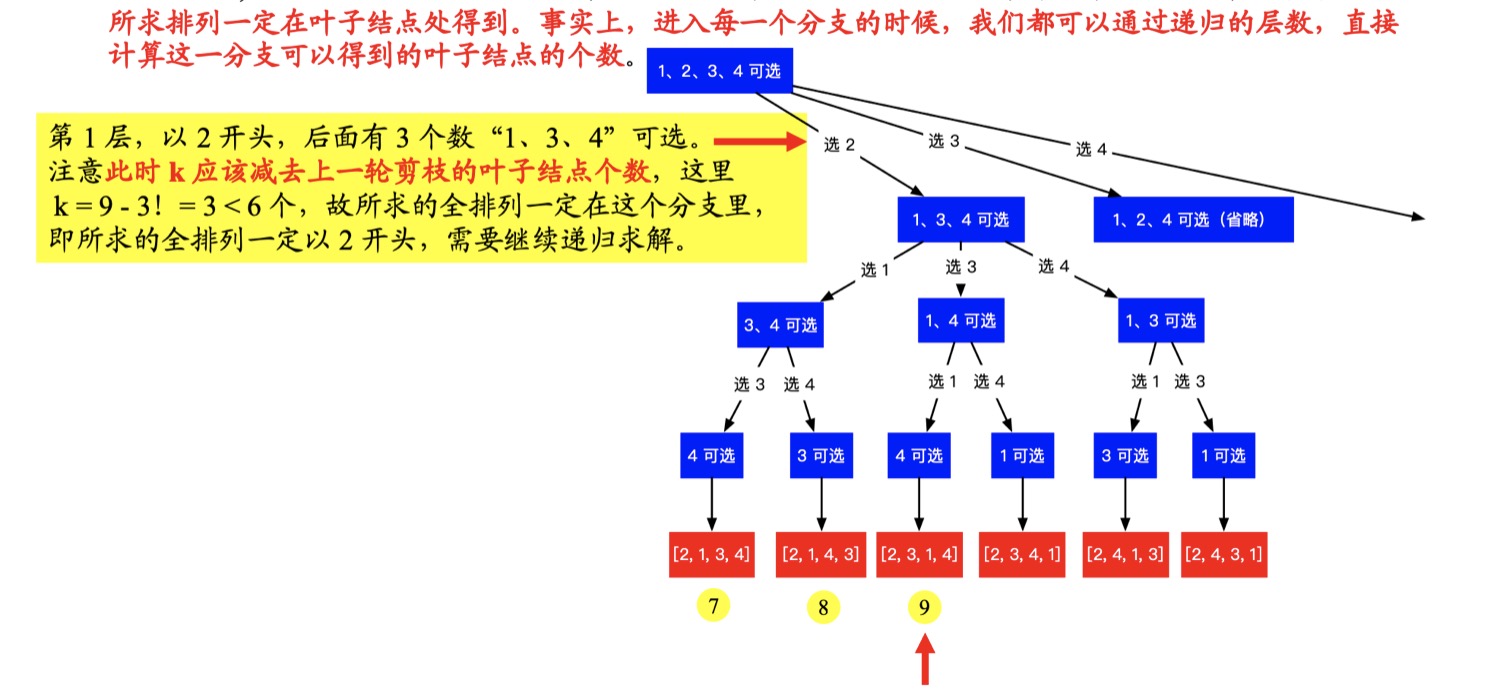
• 第二层，以 1 开头：

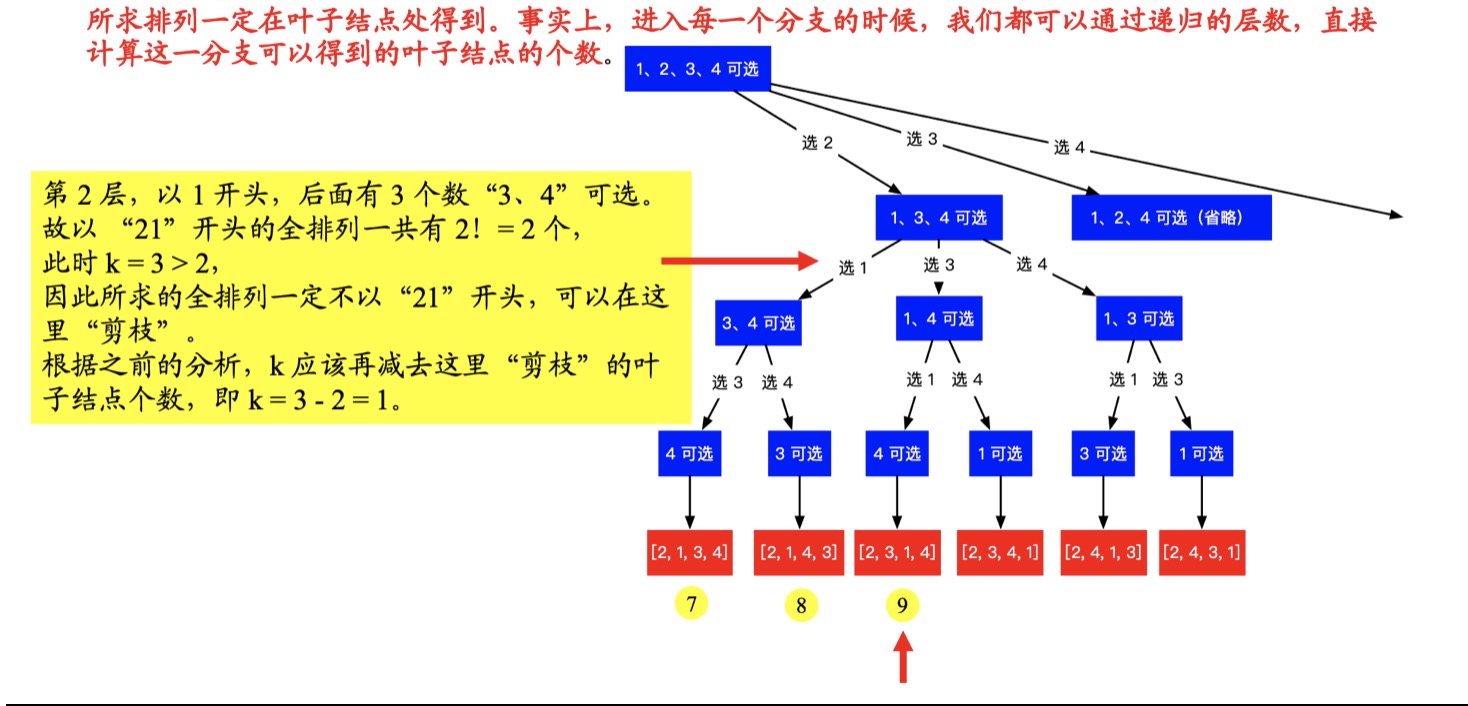
• 第三层，以 231 开头：

• 第四层，以 2314 开头：

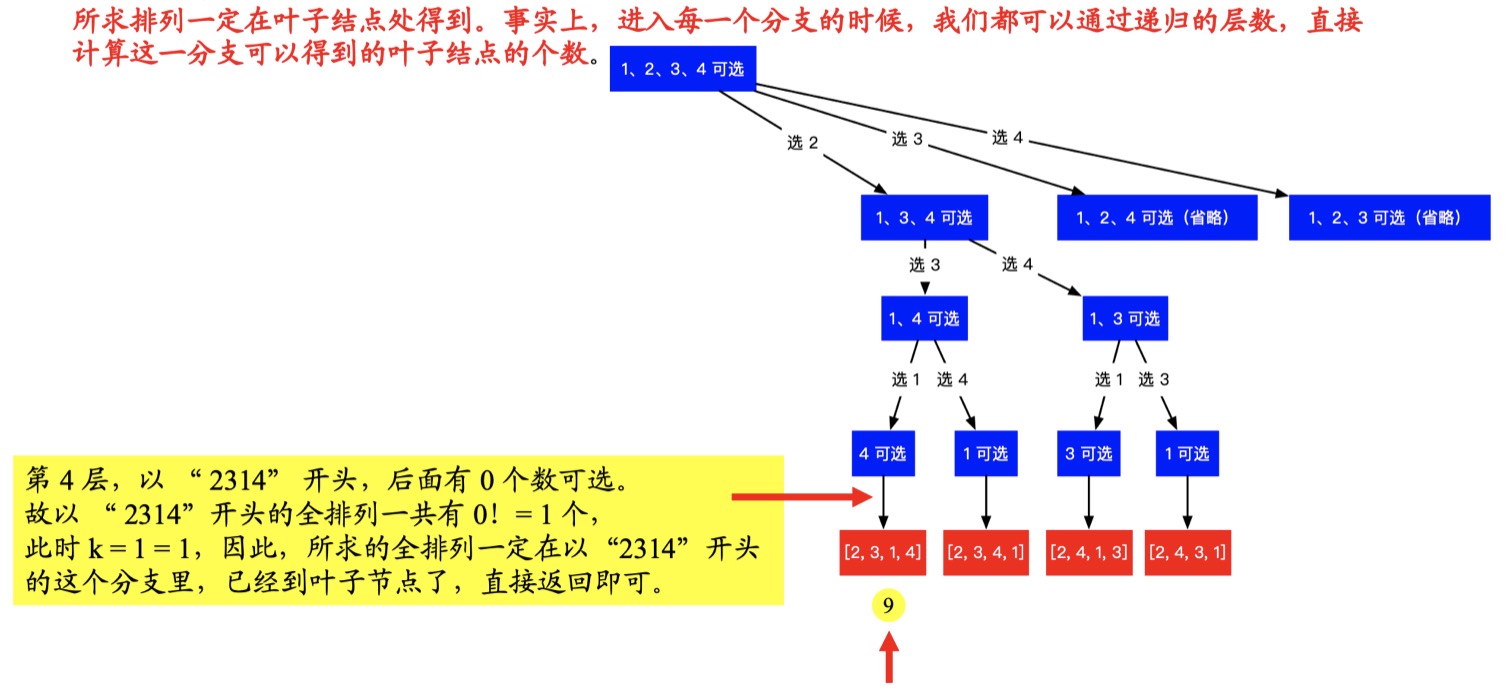
• 注意：
• • 计算阶乘的时候，可以使用循环计算。注意：0!=1，它表示了没有数可选的时候，即表示到达叶子结点了，排列数只剩下 1 个；
• • 题目中说「给定 n 的范围是 [1,9]」，可以把从 0 到 9 的阶乘计算好，放在一个数组里，可以根据索引直接获得阶乘值；
• • 编码的时候，+1 还是 −1 ，大于还是大于等于，这些不能靠猜。常见的做法是：代入一个具体的数值，认真调试。
• Java 示例：

import java.util.Arrays;

public class Solution 

    /**
     * 记录数字是否使用过
     */
    private boolean[] used;

    /**
     * 阶乘数组
     */
    private int[] factorial;

    private int n;
    private int k;

    public String getPermutation(int n, int k) 
        this.n = n;
        this.k = k;
        calculateFactorial(n);

        // 查找全排列需要的布尔数组
        used = new boolean[n + 1];
        Arrays.fill(used, false);

        StringBuilder path = new StringBuilder();
        dfs(0, path);
        return path.toString();
    


    /**
     * @param index 在这一步之前已经选择了几个数字，其值恰好等于这一步需要确定的下标位置
     * @param path
     */
    private void dfs(int index, StringBuilder path) 
        if (index == n) 
            return;
        

        // 计算还未确定的数字的全排列的个数，第 1 次进入的时候是 n - 1
        int cnt = factorial[n - 1 - index];
        for (int i = 1; i <= n; i++) 
            if (used[i]) 
                continue;
            
            if (cnt < k) 
                k -= cnt;
                continue;
            
            path.append(i);
            used[i] = true;
            dfs(index + 1, path);
            // 注意 1：不可以回溯（重置变量），算法设计是「一下子来到叶子结点」，没有回头的过程
            // 注意 2：这里要加 return，后面的数没有必要遍历去尝试了
            return;
        
    

    /**
     * 计算阶乘数组
     *
     * @param n
     */
    private void calculateFactorial(int n) 
        factorial = new int[n + 1];
        factorial[0] = 1;
        for (int i = 1; i <= n; i++) 
            factorial[i] = factorial[i - 1] * i;
        
    

② 有序数组（链表）模拟

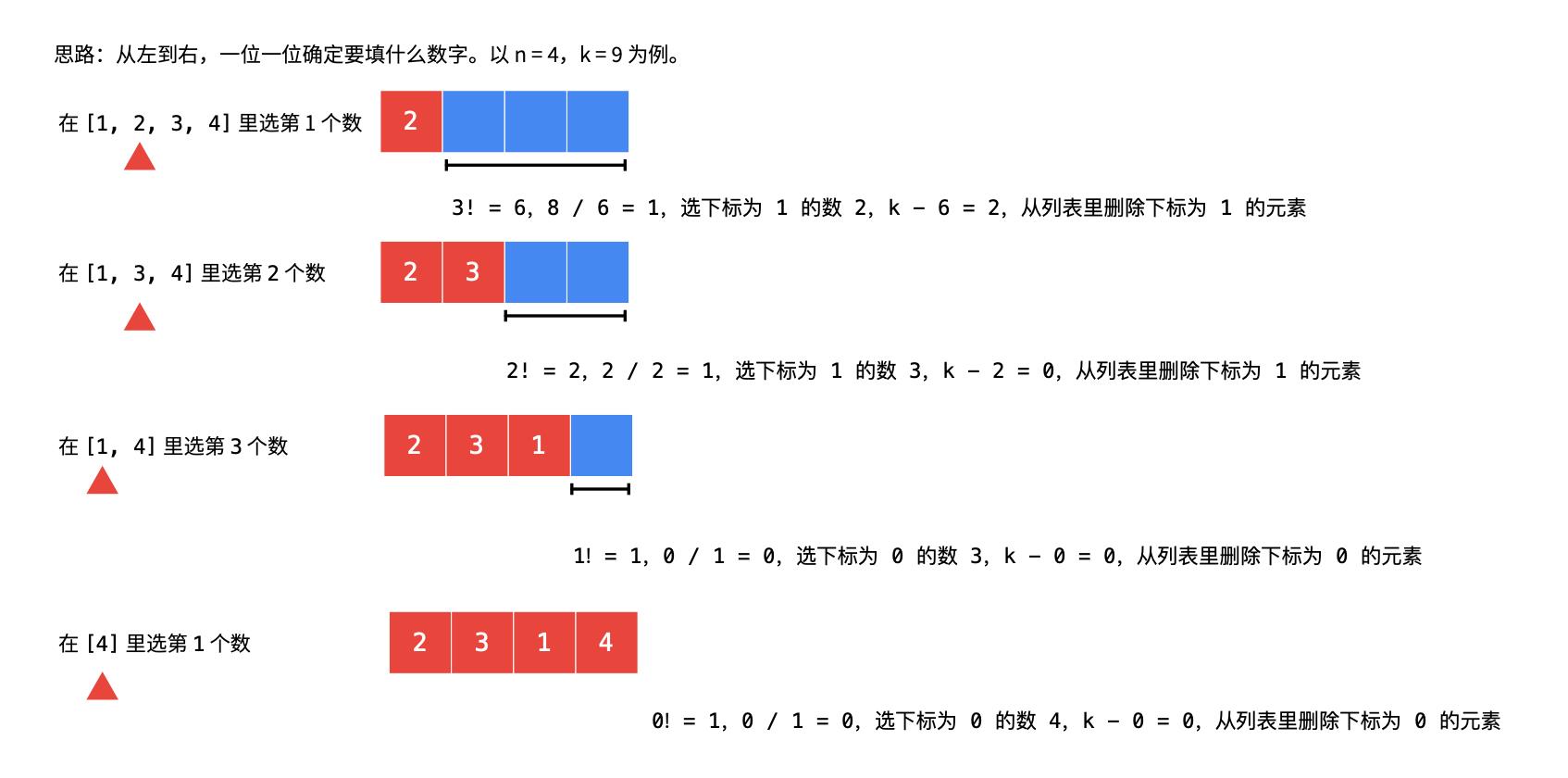
• 以 n = 4，k = 6，为例，现在确定第 1 个数字填啥。如果第 k 个数恰好是后面的数字个数的阶乘，那么第 1 个数字就只能填最小的 1。

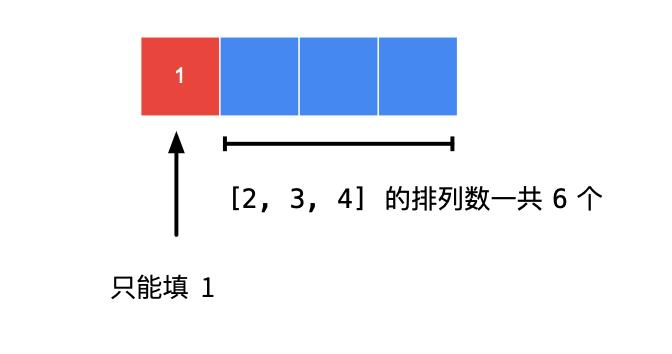
• 如果 n = 4，k = 16，现在确定第 1 个数字填啥，如果 k > 后面的数字个数的阶乘，数一数，可以跳过几个阶乘数：

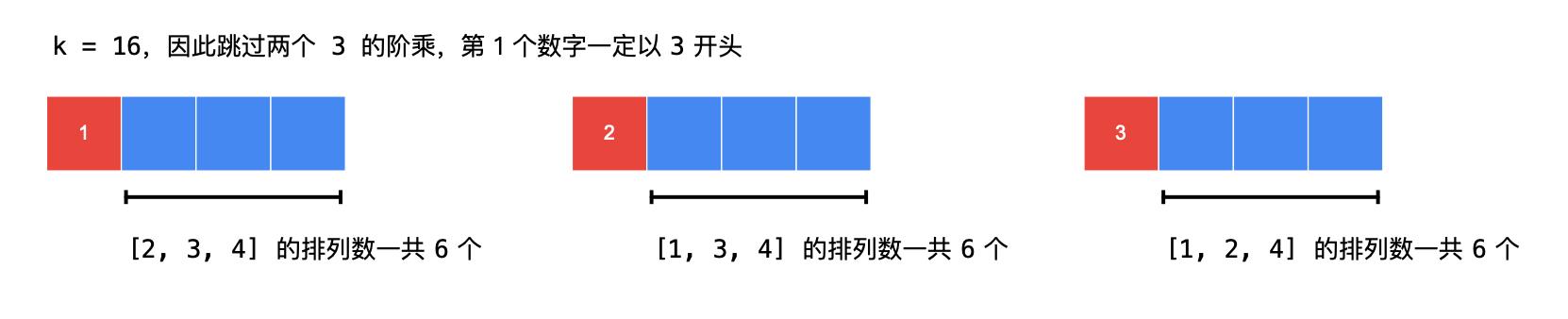
• 算法流程设计：
• • 把候选数放在一个有序列表里，从左到右根据「剩下的数的阶乘数」确定每一位填谁，公式 k / (后面几位的阶乘数) 的值 恰好等于候选数组的下标；
• • 选出一个数以后，k 就需要减去相应跳过的阶乘数的倍数；
• • 已经填好的数需要从候选列表里删除，注意保持列表的有序性（因为排列的定义是按照字典序）；
• • 由于这里考虑的是下标，第 k 个数，下标为 k - 1，一开始的时候，k–。
• 每次选出一个数，就将这个数从列表里面拿出。这个列表需要支持频繁的删除操作，因此使用双链表。在 Java 中 LinkedList 就是使用双链表实现的。
• 示例 2 如下：

• Java 示例：

import java.util.LinkedList;
import java.util.List;

public class Solution 

    public String getPermutation(int n, int k) 
        // 注意：相当于在 n 个数字的全排列中找到下标为 k - 1 的那个数，因此 k 先减 1
        k --;

        int[] factorial = new int[n];
        factorial[0] = 1;
        // 先算出所有的阶乘值
        for (int i = 1; i < n; i++) 
            factorial[i] = factorial[i - 1] * i;
        

        // 这里使用数组或者链表都行
        List<Integer> nums = new LinkedList<>();
        for (int i = 1; i <= n; i++) 
            nums.add(i);
        

        StringBuilder stringBuilder = new StringBuilder();

        // i 表示剩余的数字个数，初始化为 n - 1
        for (int i = n - 1; i >= 0; i--) 
            int index = k / factorial[i] ;
            stringBuilder.append(nums.remove(index));
            k -= index * factorial[i];
        
        return stringBuilder.toString();