数据结构和算法二叉树详解,动图+实例
Posted Linux猿
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构和算法二叉树详解,动图+实例相关的知识,希望对你有一定的参考价值。
🎈 作者:Linux猿
🎈 简介:CSDN博客专家🏆,华为云享专家🏆,Linux、C/C++、面试、刷题、算法尽管咨询我,关注我,有问题私聊!
🎈 关注专栏:图解数据结构和算法(优质好文持续更新中……)🚀
🎈 欢迎小伙伴们点赞👍、收藏⭐、留言💬
目录
二叉树是数据结构和算法中很重要的一部分,树中最典型的就数二叉树了,下面就来详细讲解下。
🍓一、什么是二叉树
二叉树(Binary tree)是一种每个节点最多有两个孩子节点的树,左右孩子节点不能随意颠倒。如下图所示:

搞错了,重来,应该是这样的,如下所示:
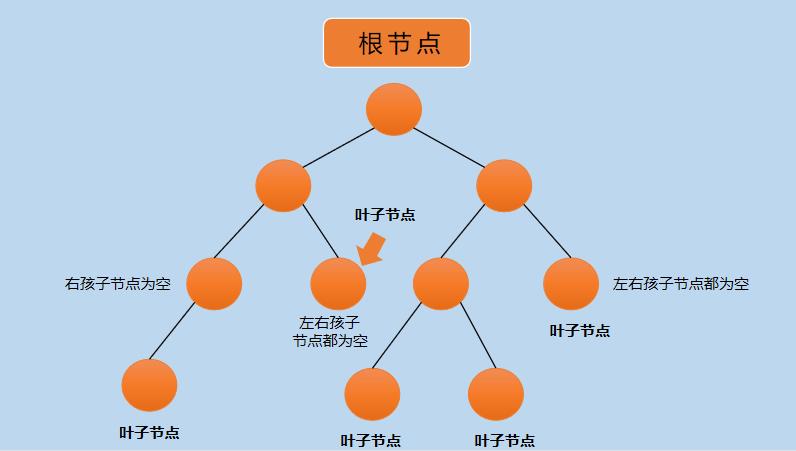
在上图中,二叉树每个节点最多有两个孩子节点,可以为空,可以只有一个左孩子或右孩子。
🔶🔶🔶🔶🔶 我是分割线 🔶🔶🔶🔶🔶
🍓二、二叉树特性
✨2.1 概念
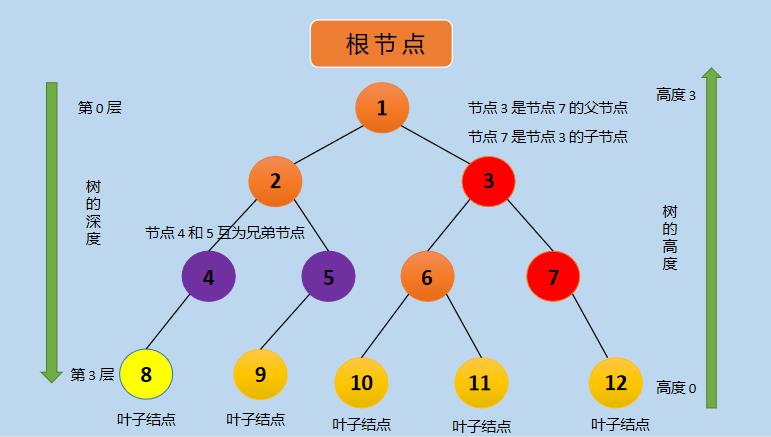
叶子节点:在一棵树中,没有孩子节点(节点度为 0)的节点称为叶子节点;
树的深度:树的深度是从根节点到最下面一层的叶子节点的层数,根节点的深度为 0 (这里不同的教程可能有差异,这里以维基百科为准);
树的高度:树的高度是从最下面一层的叶子节点到根节点的层数为高度,最下面一层的叶子节点高度为 0;
父节点/父亲节点:如果一个节点有子节点,则当前节点为子节点的父节点,根节点没有父节点;
子节点/孩子节点:与父节点相连的下一层节点为该父节点的子节点;
兄弟结点:具有相同父节点的节点,互为兄弟节点;
下面来看一张图来理解下,如下所示:
✨2.2 定理
(1)二叉树第 i 层上的节点数目最多为 2^(i-1) (i >= 1);
(2)深度为 k 的二叉树至多有 (2^k) -1 个节点 (k ≥ 1);
(3)包含 n 个节点的二叉树的高度至少为 log2(n+1);
(4)在任意一棵二叉树中,若叶子结点的个数为 N0,度为 2 的节点数为 N2,则 N0 = N2+1;
其中,第 4 条经常在考试中考到。
🔶🔶🔶🔶🔶 我是分割线 🔶🔶🔶🔶🔶
🍓三、二叉树存储
✨3.1 链式存储
typedef struct BiTNode
{
Type data;
struct BiTNode *left; // 指向左孩子
struct BiTNode *right; // 指向右孩子
}BiTNode,*BiTree;上面的结构体表示的二叉树节点中的任意节点的存储,其中:
(1)data : 表示节点存储的数据;
(2)left :指向当前节点的左孩子,如果没有则为空(NULL/nullptr);
(3)right:指向当前节点的右孩子,如果没有则为空(NULL/nullptr);
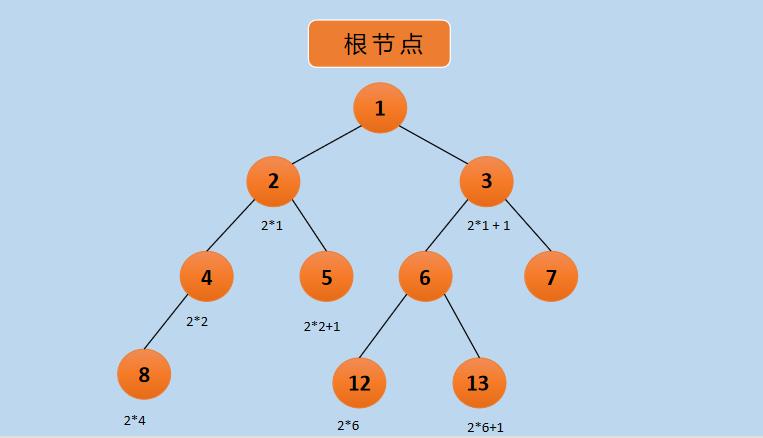
✨3.2 顺序存储
#define SIZE 1000 // 节点数
typedef Type BiTree[SIZE];上面表示的是二叉树的顺序存储结构,其中:
(1)SIZE:表示节点总数;
(2)BiTree[SIZE] :表示存储节点的数组,使用下标标识节点,一般根节点存储在下标为 1 的结点(便于计算父节点和子节点),假设父节点的下标为 i,左孩子节点则为 i*2,右孩子节点为 i*2 + 1,如下图所示:
🔶🔶🔶🔶🔶 我是分割线 🔶🔶🔶🔶🔶
🍓四、二叉树遍历
二叉树有四种遍历方法,分别是:前序遍历、中序遍历、后续遍历、层次遍历。遍历是将树的所有节点访问且仅访问一次。其中,前序遍历、中序遍历、后续遍历是按照访问根节点顺序的不同来区分的。
层次遍历是从上到下从左往右进行遍历。
✨4.1 前序遍历
前序遍历先访问根节点,然后,再以同样的方式访问左子树和右子树,直到遍历完所有节点。具体步骤如下所示:
(1)访问根节点;
(2)遍历左子树;
(3)遍历右子树;
🚩4.1.1 动图演示
下面来看一下动图演示,如下所示:
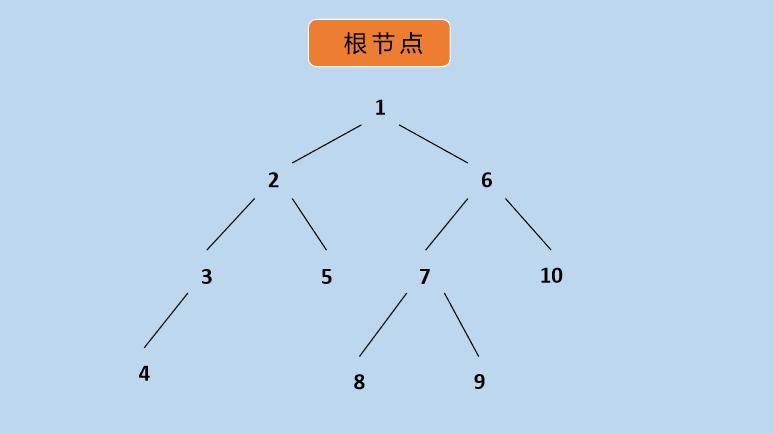
上图中,序号表示前序遍历访问的节点顺序,颜色也是按照这个顺序依次变化的。一定要记住:根->左->右。
🚩4.1.2 代码实现
这里列出前序遍历的两种实现,分别是递归版本和非递归版本,递归版本代码简洁,更好理解一些,非递归版本需要使用一个栈来模拟递归过程,原理都是一样的。
(1)递归版本
// 存储树的单个节点
struct Node {
int data; // 存储节点数据
struct Node *left; // 左孩子节点
struct Node *right; // 右孩子节点
};
// 前序遍历
void preOrder(Node *root){
if(root != NULL){ // 节点非空
cout<<root->data<<endl; //1.访问根节点
preOrder(root->left); //2.遍历左子树
preOrder(root->right); //3.遍历右子树
}
}(2)非递归版本
// 树的单个节点
struct Node {
int data; // 存储节点数据
struct Node *left; // 左孩子节点
struct Node *right; // 右孩子节点
};
// 前序遍历 非递归版本
void preOrder(Node *root)
{
stack<Node*> s; // 栈,用来模拟递归
if(root != NULL) { // 判断根节点是否为空
s.push(root);
}
while (!s.empty()) {
Node *p = s.top(); // 从栈里取出下一个要访问的节点
s.pop(); // 从栈中删除
if (p != NULL) {
cout << p->data <<endl;
if(p->right != NULL)
s.push(p->right); //先放右子树,因为是栈,先放进去的后访问
if(p->left != NULL)
s.push(p->left);
}
}
}如果有不理解栈的同学,可以看这篇讲解栈和队列的文章:
✨4.2 中序遍历
中序遍历先访问左子树,然后,访问根节点,最后,遍历右子树,直到遍历完所有节点。具体步骤如下所示:
(1)遍历左子树;
(2)访问根节点;
(3)遍历右子树;
🚩4.2.1 动图演示
下面来看一下动图演示如下所示:
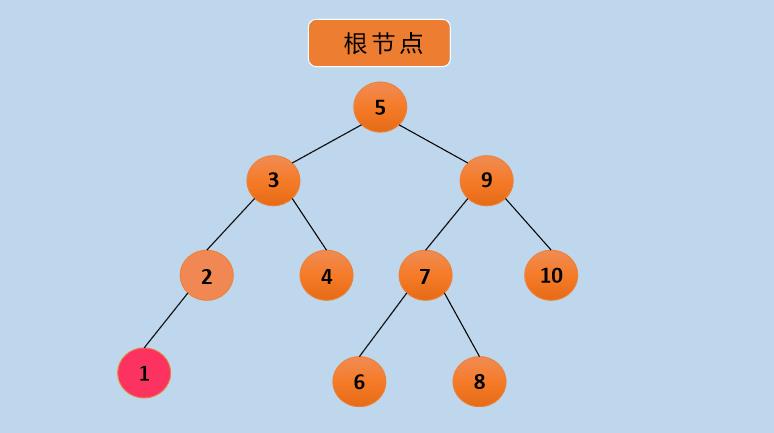
同样,上图中的序号即是中序遍历访问顺序,颜色也会相应变化。一定要记住:左->根->右。
🚩4.2.2 代码实现
这里同样也列出中序遍历的两种实现,分别是递归版本和非递归版本。
(1)递归版本
// 树的单个节点
struct Node {
int data; // 存储节点数据
struct Node *left; // 左孩子节点
struct Node *right; // 右孩子节点
};
// 中序遍历 递归版本
void inOrder(Node *root)
{
if(root != NULL) { // 判断是否为空
inOrder(root->left); // 递归遍历左子树
cout << root->data <<endl; // 访问节点
inOrder(root->right); // 递归遍历右子树
}
}(2)非递归版本
// 中序遍历 非递归版本
void inOrder(Node *root)
{
stack<Node *> s; // 栈,模拟递归
while (root != NULL || !s.empty()) {
if (root != NULL) { //1.遍历左子树
s.push(root);
root = root->left;
} else {
root = s.top();
cout << root->data <<endl; //2.访问节点
s.pop(); // 将访问过的节点从栈中删除
root = root->right; //3.遍历右子树
}
}
}✨4.3 后续遍历
前序遍历先访问根节点,然后,再以同样的方式访问左子树和右子树,直到遍历完所有节点。具体步骤如下所示:
(1)访问根节点;
(2)遍历左子树;
(3)遍历右子树;
🚩4.3.1 动图演示
下面来看一下动图演示,如下所示:
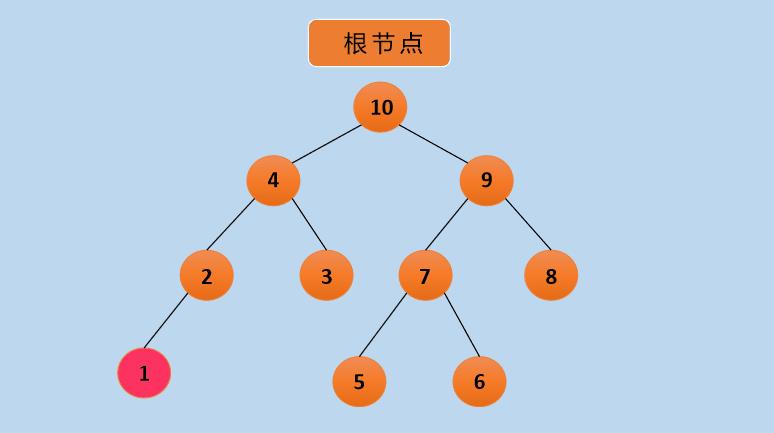
后序遍历相对于前序和中序而言,更难理解一些,一定要记住:左->右->根。
🚩4.3.2 代码实现
(1)递归版本
// 树的单个节点
struct Node {
int data; // 存储节点数据
struct Node *left; // 左孩子节点
struct Node *right; // 右孩子节点
};
// 后续遍历 递归版本
void postOrder(Node *root)
{
if(root != NULL) { // 判断是否为空
postOrder(root->left); // 遍历左子树
postOrder(root->right); // 遍历右子树
cout << root->data <<endl; // 访问节点
}
}(2)非递归版本
// 树的单个节点
struct Node {
int data; // 存储节点数据
struct Node *left; // 左孩子节点
struct Node *right; // 右孩子节点
};
// 后序遍历 非递归版本
void postOrder(Node* root){
Node* curt = root;
Node* pos = NULL;
stack<Node*> s; // 栈,用于模拟递归
while (curt || !s.empty()) {
while (curt) {
s.push(curt);
curt = curt->left;
}
Node* top = s.top();
if(top->right == NULL || top->right == pos) {
cout<<top->data<<endl;
pos = top;
s.pop();
} else {
curt = top->right;
}
}
}✨4.4 层次遍历
二叉树层次遍历的顺序是按照树的深度,从上到下,从左到右进行遍历的。
🚩4.4.1 非递归版本
// 树的单个节点
struct Node {
int data; // 存储节点数据
struct Node *left; // 左孩子节点
struct Node *right; // 右孩子节点
};
// 层次遍历 非递归版本
void levelTraversal(Node* root)
{
queue<Node*> q; // 队列
q.push(root);
while (!q.empty()) { // 非空才循环
Node* curt = q.front(); // 取出最前面的元素
q.pop(); // 删除访问的元素
cout<<curt->data<<endl; // 访问当前元素
if (curt->left) // 判断左孩子
q.push(curt->left);
if(curt->right)
q.push(curt->right); // 判断右孩子
}
}🚩4.4.2 动图演示
下面来看一下层次遍历的动图演示,如下所示:
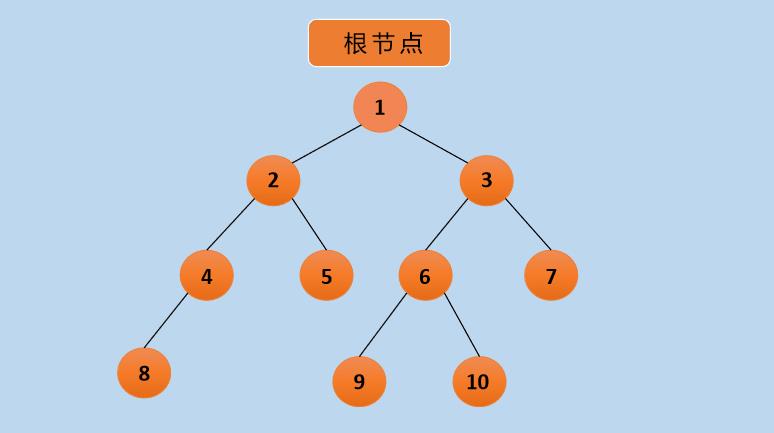
层次遍历是按照由上到下,由左到右进行遍历,正好符合广度优先搜索的思路。
🍓五、特殊二叉树
在众多的二叉树中,有写二叉树具有一些独特的特性,这样的二叉树有:满二叉树和完全二叉树,下面就来看一下。
✨5.1 满二叉树
满二叉树除了叶子节点外,非叶子节点都有两个孩子节点,如下所示:
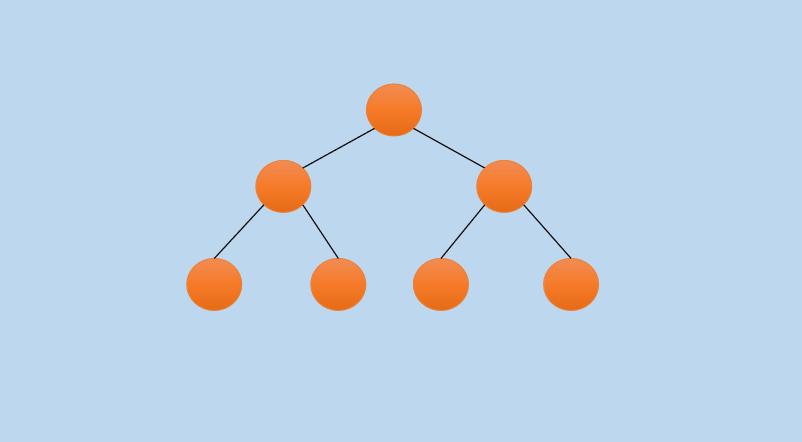
上图是一个深度为 3 的满二叉树,可以看到,除叶子节点外,非叶子节点都有两个孩子。
✨5.2 完全二叉树
完全二叉树是除了最后一层外,其它层的节点数都有两个孩子节点,如下图所示:
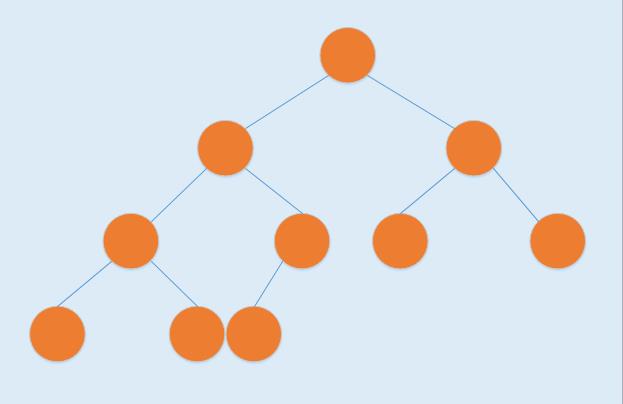
🍓六、实战演练
✨6.1 求二叉树深度
假设有一二叉树,如下所示:
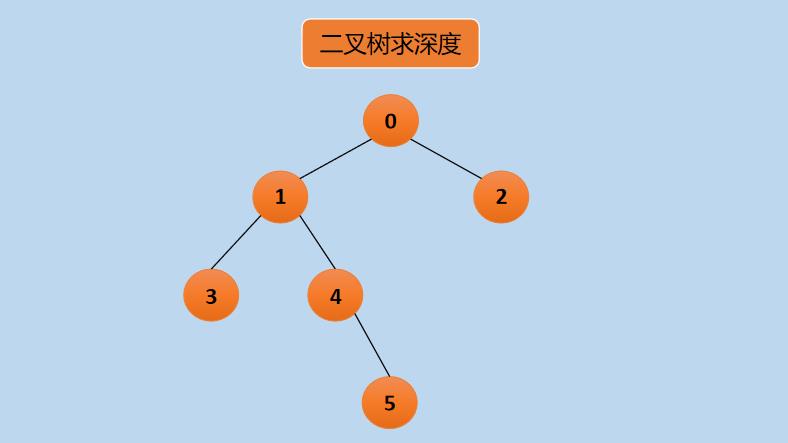
🚩6.1.1 递归版本
代码实现(递归版本)
#include <iostream>
using namespace std;
// 二叉树节点存储
typedef struct BiTNode
{
int data;
struct BiTNode *left; // 指向左孩子
struct BiTNode *right; // 指向右孩子
}BiTNode,*BiTree;
// 求二叉树深度
int binaryTreeDepth(BiTree root)
{
if(root == nullptr) // 空的话返回 0
return 0;
else {
int leftDepth = binaryTreeDepth(root->left); // 求左子树的深度
int rightDepth = binaryTreeDepth(root->right); // 求右子树的深度
return max(leftDepth, rightDepth) + 1;
}
}
int main() {
// 创建一个二叉树
BiTNode * root = new(BiTNode);
BiTNode * node1 = new(BiTNode);
BiTNode * node2 = new(BiTNode);
BiTNode * node3 = new(BiTNode);
BiTNode * node4 = new(BiTNode);
BiTNode * node5 = new(BiTNode);
root->left = node1;
root->right = node2;
node1->left = node3;
node1->right = node4;
node4->left = nullptr;
node4->right = node5;
node2->left = nullptr;
node2->right = nullptr;
node3->left = nullptr;
node3->right = nullptr;
node5->left = nullptr;
node5->right = nullptr;
// 调用求二叉树深度
cout<<"Binary Tree Depth = "<<binaryTreeDepth(root)-1<<endl; // 减 1 是因为从 0 开始计算的深度
}🚩6.1.2 非递归版本
代码实现(非递归)
#include <iostream>
#include <queue>
using namespace std;
// 二叉树节点存储
typedef struct BiTNode
{
int data;
struct BiTNode *left; // 指向左孩子
struct BiTNode *right; // 指向右孩子
}BiTNode,*BiTree;
// 求二叉树深度 递归版本
int binaryTreeDepth(BiTree root)
{
if(root == nullptr) // 空的话返回 0
return 0;
else {
int leftDepth = binaryTreeDepth(root->left); // 求左子树的深度
int rightDepth = binaryTreeDepth(root->right); // 求右子树的深度
return max(leftDepth, rightDepth) + 1;
}
}
//求二叉树深度 非递归版本
int binaryTreeDepth(BiTree root)
{
queue<BiTree> q;
if(!root) return 0;
q.push(root);
int depth = 0;
while(!q.empty()) {
int num = q.size();
depth++;
while(num--) {
BiTree curt = q.front();
q.pop();
if(curt->left) q.push(curt->left);
if(curt->right) q.push(curt->right);
}
}
return depth;
}
int main() {
// 创建一个二叉树
BiTNode * root = new(BiTNode);
BiTNode * node1 = new(BiTNode);
BiTNode * node2 = new(BiTNode);
BiTNode * node3 = new(BiTNode);
BiTNode * node4 = new(BiTNode);
BiTNode * node5 = new(BiTNode);
root->left = node1;
root->right = node2;
node1->left = node3;
node1->right = node4;
node4->left = nullptr;
node4->right = node5;
node2->left = nullptr;
node2->right = nullptr;
node3->left = nullptr;
node3->right = nullptr;
node5->left = nullptr;
node5->right = nullptr;
// 调用求二叉树深度
cout<<"Binary Tree Depth = "<<binaryTreeDepth(root)-1<<endl; // 减 1 是因为从 0 开始计算的深度,如果从1开始计算,则不用减 1 操作
}✨6.2 翻转二叉树
假设有一棵二叉树,如下所示:
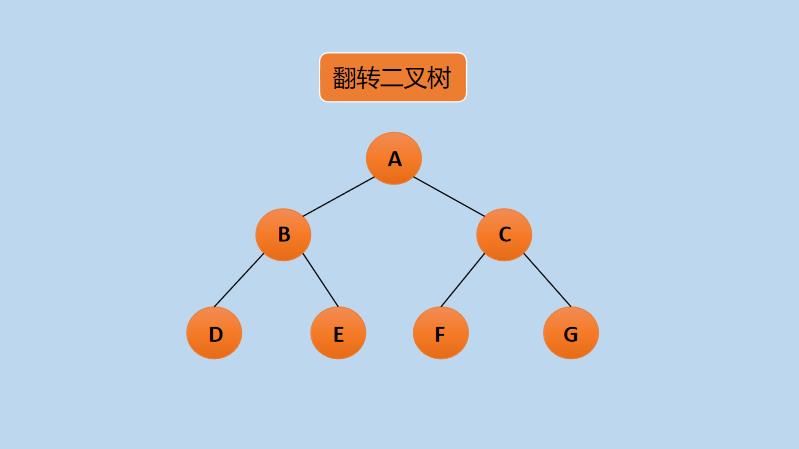
上图中,使用大写字母来标识每一个节点,翻转上图的二叉树后,如下所示:
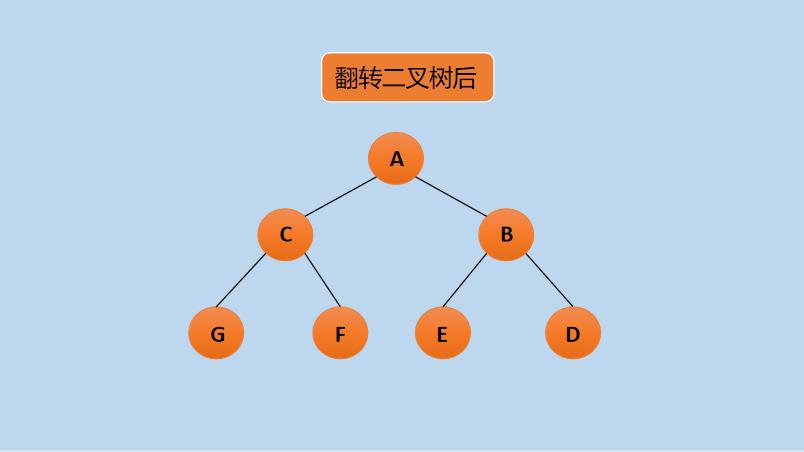
在图中,实现了二叉树的翻转,所谓 “翻转”,实质上是将每个节点的左右孩子节点交换,下面就来看下代码实现,如下所示:
#include <iostream>
using namespace std;
// 二叉树节点存储
typedef struct BiTNode
{
char data;
struct BiTNode *left; // 指向左孩子
struct BiTNode *right; // 指向右孩子
}BiTNode,*BiTree;
class Solution {
public:
BiTNode* invertTree(BiTNode* root) {
if (root == nullptr) {
return nullptr;
}
BiTNode* left = invertTree(root->left); // 递归处理左子树
BiTNode* right = invertTree(root->right); // 递归处理右子树
root->left = right; // 交换当前节点的左右子树
root->right = left;
return root;
}
};
// 前序遍历输出二叉树
void printTree(BiTNode* root)
{
if(root == nullptr)
return;
cout<<root->data<<" ";
if(root->left)
printTree(root->left);
if(root->right)
printTree(root->right);
}
int main()
{
// 创建二叉树
BiTNode* rootA = new(BiTNode);
BiTNode* nodeB = new(BiTNode);
BiTNode* nodeC = new(BiTNode);
BiTNode* nodeD = new(BiTNode);
BiTNode* nodeE = new(BiTNode);
BiTNode* nodeF = new(BiTNode);
BiTNode* nodeG = new(BiTNode);
rootA->left = nodeB;
rootA->right = nodeC;
rootA->data = 'A';
nodeB->left = nodeD;
nodeB->right = nodeE;
nodeB->data = 'B';
nodeC->left = nodeF;
nodeC->right = nodeG;
nodeC->data = 'C';
nodeD->left = nullptr;
nodeD->right = nullptr;
nodeD->data = 'D';
nodeE->left = nullptr;
nodeE->right = nullptr;
nodeE->data = 'E';
nodeF->left = nullptr;
nodeF->right = nullptr;
nodeF->data = 'F';
nodeG->left = nullptr;
nodeG->right = nullptr;
nodeG->data = 'G';
// 翻转前输出
cout<<"翻转前 ";
printTree(rootA);
cout<<endl;
Solution obj;
obj.invertTree(rootA);
// 翻转后输出
cout<<"翻转后 ";
printTree(rootA);
cout<<endl;
return 0;
}
输出结果为:
linuxy@linuxy:~$ ./inverBinary
翻转前 A B D E C F G
翻转后 A C G F B E D
linuxy@linuxy:~$输出的遍历结果是前序遍历的结果,可以看到,将二叉树每个节点的左右子树都翻转了。
🔶🔶🔶🔶🔶 我是分割线 🔶🔶🔶🔶🔶
🍓七、总结
好了,上面就是所有二叉树讲解的所有内容了,在掌握基本的二叉树概念后,还需要多实战,多练习。
关注👇👇👇👇👇👇,获取更多优质内容🤞(比心)!
以上是关于数据结构和算法二叉树详解,动图+实例的主要内容,如果未能解决你的问题,请参考以下文章
❤️《算法和数据结构》小白零基础教学,三十张彩图,C语言配套代码,之 二叉树详解❤️(建议收藏)
❤️《算法和数据结构》小白零基础教学,三十张彩图,C语言配套代码,之 二叉树详解❤️(建议收藏)
八大排序算法——堆排序(动图演示 思路分析 实例代码java 复杂度分析)
二万字《算法和数据结构》三张动图,三十张彩图,C语言基础教学,之 二叉搜索树详解 (建议收藏)