快速了解什么是RSA加密算法

Posted 2021-11-01 小哈里

1、什么是RSA

加密算法有对称加密和非对称加密。

• 对称加密是指发送方和接收方使用相同的一种规则对信息进行处理，因为双方使用的是相同的规则和密钥，所以一旦密钥泄露，那么再强大的加密也将毫无用处。
• 所有后来就有了过度的密钥交换算法和最后的非对称加密，简而言之就是：通信双方通过计算生成出一个相同的共享密钥来进行交换信息。比如RSA就是通过公钥来加密，私钥来解密，这样公钥是公开的，私钥只有自己才有，就避免了规则泄露造成的解密。

区分古典密码学和现代密码的关键特性：

• 古典密码体制中，数据的保密基于加密算法的保密。 现代密码体制中，数据的安全基于密钥而不是算法的保密。

RSA算法的历史：

• RSA 是 1977 年由罗纳德 · 李维斯特（Ron Rivest）、阿迪 · 萨莫尔（Adi Shamir）和伦纳德 · 阿德曼（Leonard Adleman）一起提出的。RSA 就是他们三人姓氏开头字母拼在一起组成的。
• RSA 算法的可靠性由极大整数因数分解的难度决定。 对一极大整数做因数分解愈困难，RSA 算法愈可靠。目前只有短的 RSA 密钥才可能被强力方式解破（目前被破解的最长RSA密钥是768个二进制位。），到 2021 年为止，还没有任何可靠的攻击 RSA 算法的方式。

• RSA算法可以说是地球上最重要的算法之一，是数据通信和网络安全的基石。

2、RSA的原理和实现

背景数学知识（懂的可以跳过）：

• 逆元定义：也叫膜反素数，逆元素是指一个可以取消另一给定元素运算的元素, 比如一个数和其倒数互为乘法逆元ax=1,x=1/a，一个数和其相反数互为加法逆元等等a+x=0,x=-a。
  模意义下的逆元：因为任何数与1的乘积均为其本身，所以a%p意义下的乘法逆元为x满足ax%p==1。 $$ax\equiv 1(modp)$$
  逆元可以由费马小定理（p为质数），或者扩展欧几里得求。
• 欧拉函数：给定一个正整数n,求1-n中与n互质的数的个数，记作f(n)。
• 欧拉定理：

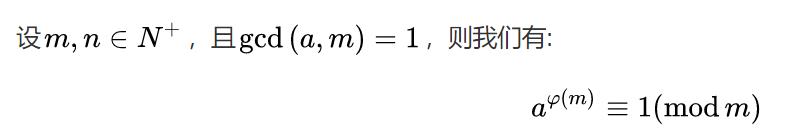
RSA的原理：

python代码