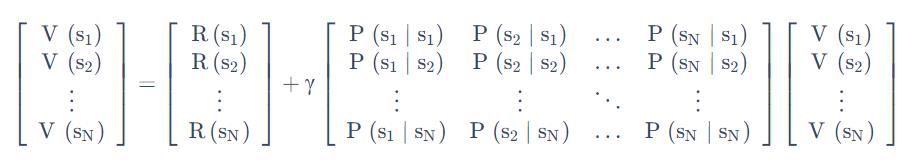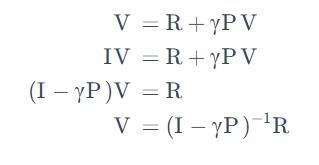强化学习笔记：马尔可夫过程 &马尔可夫奖励过程

Posted 2021-10-31 UQI-LIUWJ

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了强化学习笔记：马尔可夫过程 &马尔可夫奖励过程相关的知识，希望对你有一定的参考价值。

1 马尔可夫性质（Markov Property）

我们设状态的历史为 $h_{t}=\left\{s_{1}, s_{2}, s_{3}, \ldots, s_{t}\right\}$ （包含了之前的所有状态）

如果一个状态转移是符合马尔可夫性质的，也就是满足如下条件：

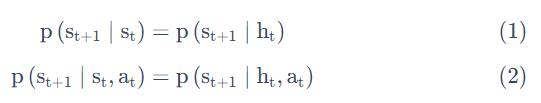
也就是说，从当前状态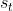转移到状态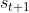的概率，就直接等于它之前所有的状态转移到状态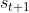的概率。

换句话说，如果一个过程满足马尔可夫性质，那么就是说，这个过程未来状态和过去状态是独立的。未来的状态只取决于现在的状态。

2 马尔可夫链（Markov Chain）

这个图里面有四个状态，这四个状态从s1,s2,s3,s4 之间互相转移。转移概率就是边的权重。

2.1 状态转移矩阵

我们可以用状态转移矩阵来描述转移概率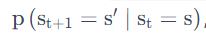

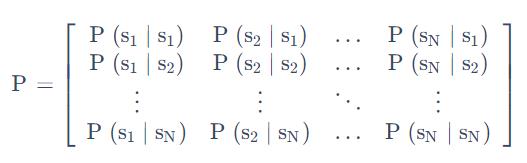
它每一行其实描述了是从一个节点到达所有其它节点的概率。

3 马尔可夫链

上图是一个马尔可夫链的例子，我们这里有七个状态。比如说从 s1 开始到s2 ，它有 0.4 的概率，然后它有 0.6 的概率继续停留在它当前的状态。

所以给定了这个状态转移的马尔可夫链后，我们可以对这个链进行采样，这样就会得到一串的轨迹。

4 马尔可夫奖励过程（Markov Reward Process）

马尔可夫奖励过程(Markov Reward Process, MRP) 是马尔可夫链再加上了一个奖励函数。

在 MRP 中，转移矩阵和状态都是跟马尔可夫链一样的，多了一个奖励函数(reward function)

这里是我们刚才看的马尔可夫链，如果把奖励也放上去的话，就是说到达每一个状态，我们都会获得一个奖励。

这里我们可以设置对应的奖励，比如说到达 s1 状态的时候，可以获得 5 的奖励，到达 s7 的时候，可以得到 10 的奖励，其它状态没有任何奖励。

因为这里状态是有限的，所以我们可以用向量R=[5,0,0,0,0,0,10] 来表示这个奖励函数，这个向量表示了每个点的奖励大小。

4.1 return &value function

4.1.1 horizon

一个回合的长度（每个回合最大的时间步数），它是由有限个步数决定的。

4.1.2 return

把奖励进行折扣后所获得的收益。Return 可以定义为奖励的逐步叠加

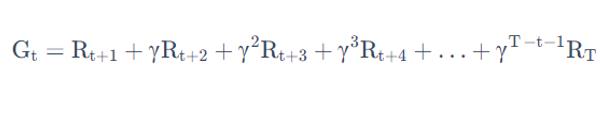
越往后得到的奖励，折扣得越多。这说明我们其实更希望得到现有的奖励，未来的奖励就要把它打折扣。

4.1.3 state value function

当我们有了 return 过后，就可以定义一个状态的价值了，就是 state value function。

对于 MRP，state value function 被定义成是 return 的期望

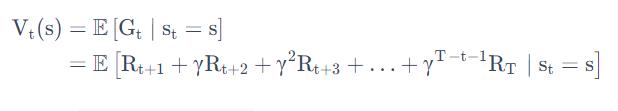
Gt 是之前定义的 discounted return，我们这里取了一个期望，期望就是说从这个状态开始，你有可能获得多大的价值。

这个期望也可以看成是对未来可能获得奖励的当前价值的一个表现，就是当你进入某一个状态过后，你现在就有多大的价值。

这里的Value值怎么计算呢？我们看后面的4.4

4.2 为什么return有折扣因子？

有些马尔可夫过程是带环的，它并没有终结，我们想避免这个无穷的奖励。（到某一个时刻T之后，reward接近于0，轨迹停止）
我们对未来的评估不一定是准确的，我们不一定完全信任我们的模型。因为这种不确定性，所以我们对未来的预估增加一个折扣。我们想把这个不确定性表示出来，希望尽可能快地得到奖励，而不是在未来某一个点得到奖励。
如果这个奖励是有实际价值的，我们可能是更希望立刻就得到奖励，而不是后面再得到奖励（现在的钱比以后的钱更有价值）。【类比：通货膨胀，现在是10块钱和十年后的10块钱】
有些时候可以把这个系数设为 0，γ=0：我们就只关注了它当前的奖励。我们也可以把它设为 1，γ=1：对未来并没有折扣，未来获得的奖励跟当前获得的奖励是一样的。

Discount factor 可以作为强化学习 agent 的一个超参数来进行调整，然后就会得到不同行为的 agent。

4.3 马尔科夫奖励过程举例

和4开篇说的例子是一样的：进入第一个状态的时候会得到 5 的奖励，进入第七个状态的时候会得到 10 的奖励，其它状态都没有奖励。

我们现在可以计算每一个轨迹得到的奖励，比如我们对于这个s4,s5,s6,s7 轨迹的奖励进行计算，这里折扣系数是 0.5。

在 4 的时候，奖励为零。

下一个状态s5 的时候，因为我们已经到了下一步了，所以我们要把 s5 进行一个折扣，s5 本身也是没有奖励的。

然后是到 s6，也没有任何奖励，折扣系数应该是。

到达s7 后，我们获得了一个奖励，但是因为s7 这个状态是未来才获得的奖励，所以我们要进行三次折扣。

所以对于这个轨迹，它的 return 就是一个 1.25，类似地，我们可以得到其它轨迹的 return 。

4.4 贝尔曼等式（Bellman Equation）【动态规划方程】

我们前面知道了，一个马尔科夫奖励过程的value function为：

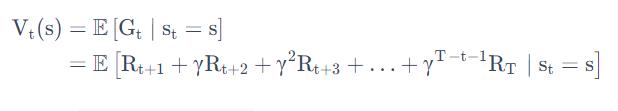
于是我们可以稍微改造一下

整理一下，就有：

这个就是贝尔曼等式，未来打了折扣的奖励加上当前立刻可以得到的奖励，就组成了这个 Bellman Equation。

        假设有一个马尔可夫转移矩阵是右边这个样子，Bellman Equation 描述的就是当前状态到未来状态的一个转移。

        假设我们当前是在s1，那么它只可能去到三个未来的状态：有 0.1 的概率留在它当前这个位置，有 0.2 的概率去到s2 状态，有 0.7 的概率去到s4 的状态

        所以我们要把这个转移乘以它未来的状态的价值，再加上它的 immediate reward 就会得到它当前状态的价值。

4.4.1 矩阵形式理解贝尔曼等式&贝尔曼等式的解析解

我们可以把 Bellman Equation 写成一种矩阵的形式

对于第i行，有：

也即：

当我们把 Bellman Equation 写成矩阵形式后，可以直接求解：

于是我们得到了一组解析解：

我们可以通过矩阵求逆把这个 V 的这个价值直接求出来。但是一个问题是这个矩阵求逆的过程的复杂度是 O(N^3)。这导致处理大矩阵的时候是非常困难的。

所以这种通过解析解去求解的方法只适用于很小量的 MRP。