测试简单混沌电路系统的低频特性

Posted 2021-10-23 卓晴

 

§01 简单混沌电路

---

  在 测试简易混沌振荡电路一些因素的影响 中对于 两个晶体管组成的混沌电路 的多个因素进行测量，比如工作电压、晶体管型号、耦合电阻R3的范围等。为了能够对于混点信号进行测量与分析，下面对于该信号的频率范围进行测试。

一、混沌电路

1、建立混沌电路

（1）电路图

  下面给出了前面实验中使用到的混沌电路图。它的工作的基本频率是在相移单管正弦振荡器的基础上。

▲ 图1.1.1 双晶体管混沌电路图

2、电路元器件参数

（1）电容

  为了获得低频信号，将其中的电容容量增加。下面以下电容来实现$C_1,C_2,C_3,C_4$。

▲ 图1.1.2 电路中的C1 ~ C4电容

  使用SmartTweezer测量上面个电容的容量：

【表1-1-2-1 电路中的电容参数】

C1	C2	C3	C4
211.8nF	218.3nF	217.7nF	84.48nF

（2）晶体管

【表1-1-2-2 电路中的晶体管】

序号	hFE	Vbe	I
1	332	655mV	2.1mA
2	339	649mV	2.1mA

（3）电阻

【表1-1-2-3 电路中的电阻】

R1	R2	R3	R4
5051	5027	9920	9847

3、面包板上电路

  在面包板上搭建测试电路。

▲ 图1.1.3 面包板上的搭建的测试电路

二、测量电路

1、电路振荡信号

• 工作电压： +9V。

（1）振荡波形

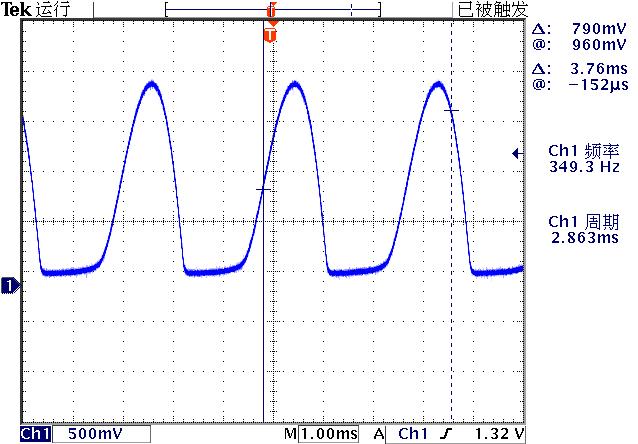
▲ 图1.2.1 Q1的c信号波形

（2）振荡频率

  振荡频率：349.07Hz。

2、工作电压与频率

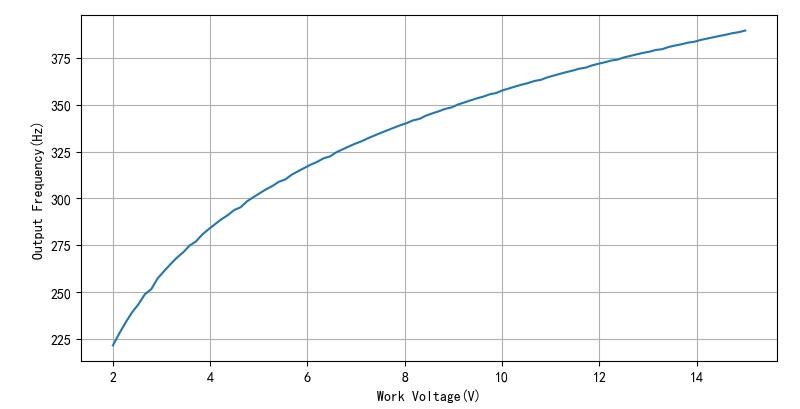
▲ 图1.2.2 工作电压与振荡频率

3、不同工作下Q1输入电阻

测量方法：

工作电压：+5V
测量方法：SmartTweezer
耦合方式：10uF耦合

（1）测量不同频率下的输入电阻

不同的测量频率：

100Hz：2.712k
120Hz：2.602k
1000Hz：224.3Ω
10kHz：9.642Ω

 

§02 理论分析

---

一、相移RC网络

1、等效电路

  下面是移相RC网络等效电路图，产生振荡的条件是$U_c$的相位与$U_{rb}$之间相移 180°。

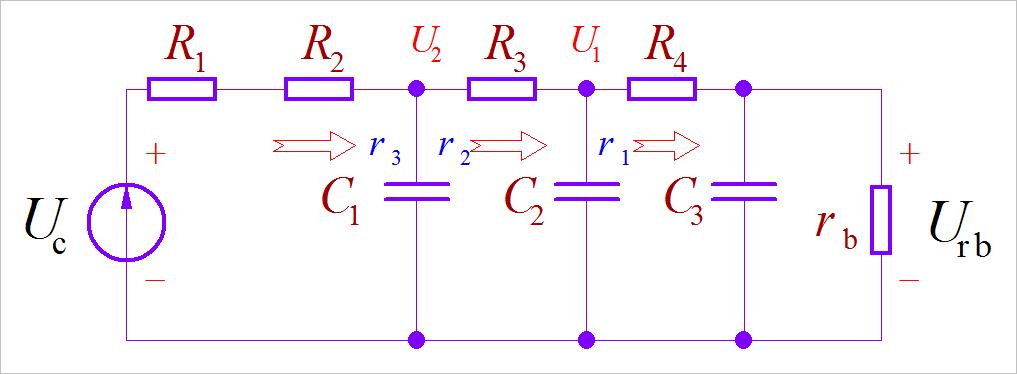
▲ 图2.1.1 相移电阻电容网络

2、传递函数

  使用前面电路中的参数计算 $U_C,U_{rb}$之间的电路传递函数。

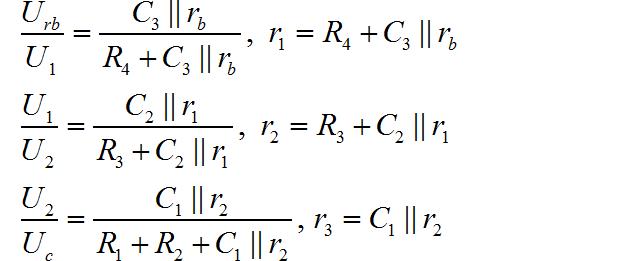
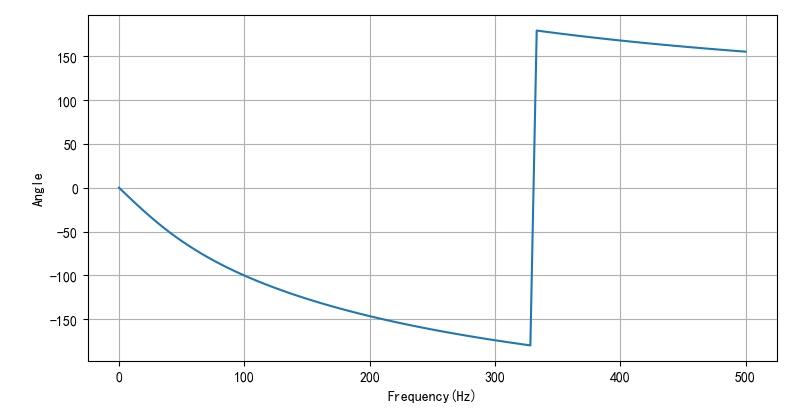
▲ 图2.1.2 不同频率与相位
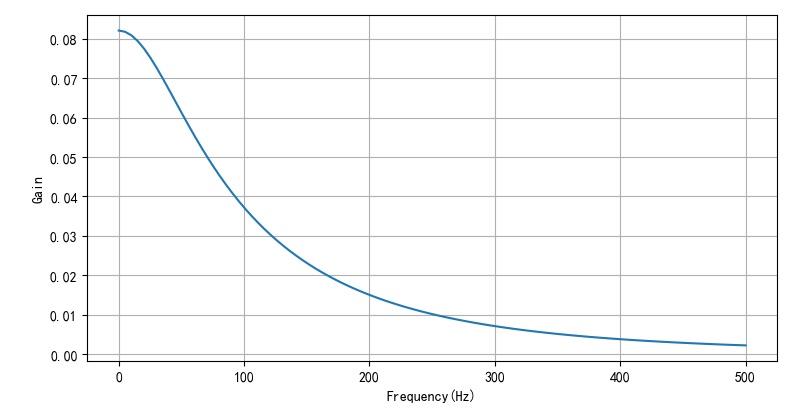
▲ 图2.1.3 不同频率与增益

3、数值求解

相移180度参数：

频率（Hz）：329.0Hz
Gain：0.00585； 171

二、电路参数扫描

1、Q1输入电阻rb

  对于不同rb 对于振荡频率的影响。

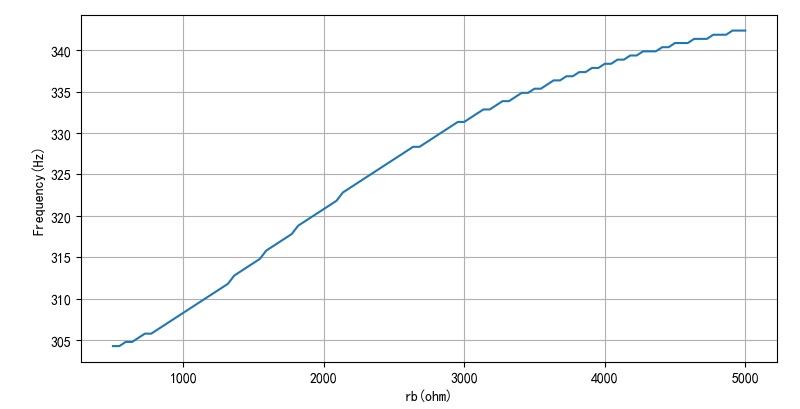
▲ 图2.2.1 不同的Q1的输入电阻对于振荡频率影响

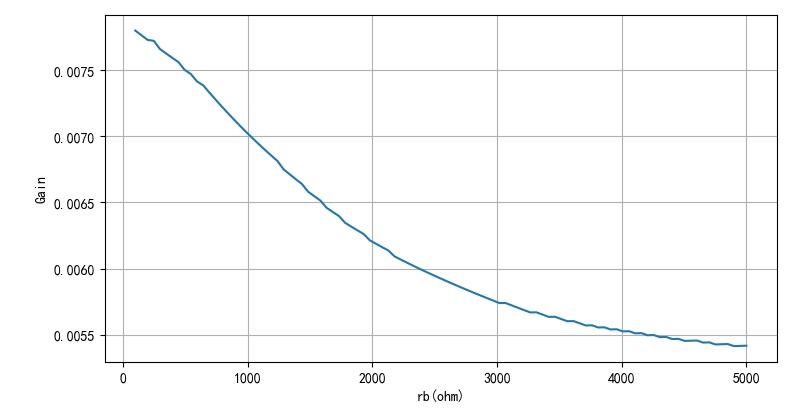
▲ 图2.2.2 不同的Q1的输入电阻对于增益的影响

  上面的计算结果与通常情况下前面测试的结果正好相反。

 

§03 搭建混沌电路

---

一、电路搭建

▲ 图3.1.1 面包板上的搭建的测试电路

二、测量波形

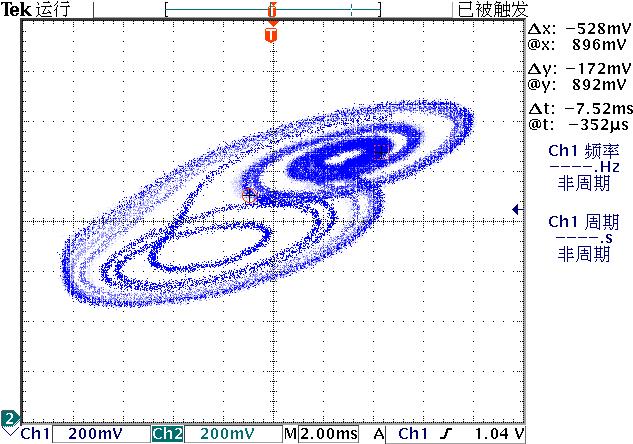
▲ 图3.2.1 Q1集电极以及C1上的电压轨迹

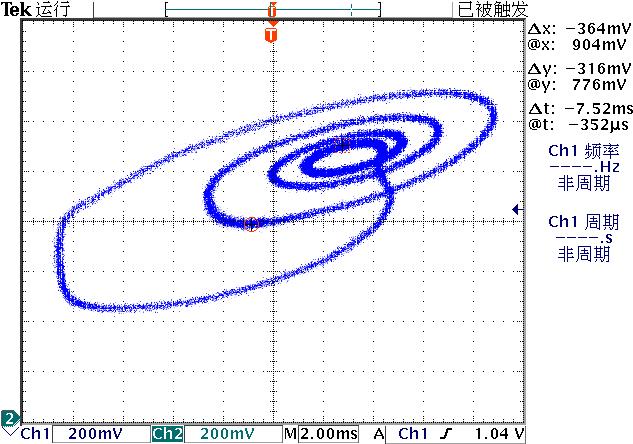
▲ 图3.2.2 Q1集电极以及C1上的电压轨迹

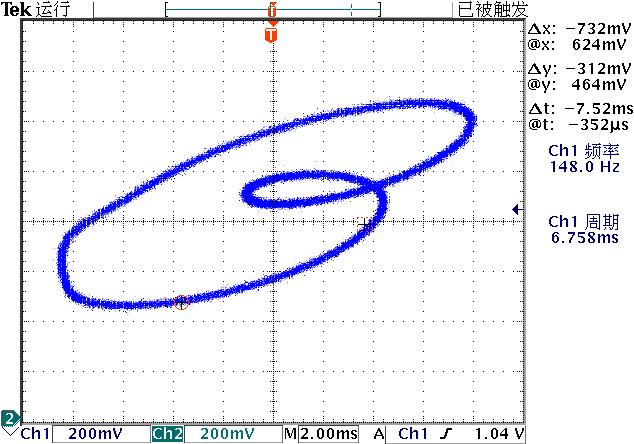
▲ 图3.2.3 Q1集电极以及C1上的电压轨迹

 

※ 测试结论 ※

---

  修改了双晶体管混沌电路参数，电路的振荡频率降低到300Hz左右。

  通过理论分析，测试了电路参数与振荡频率之间的关系。

---

■ 相关文献链接:

• 测试简易混沌振荡电路一些因素的影响
• 两个晶体管组成的混沌电路

● 相关图表链接:

• 图1.1.1 双晶体管混沌电路图
• 图1.1.2 电路中的C1 ~ C4电容
• 表1-1-2-1 电路中的电容参数
• 表1-1-2-2 电路中的晶体管
• 表1-1-2-3 电路中的电阻
• 图1.1.3 面包板上的搭建的测试电路
• 图1.2.1 Q1的c信号波形
• 图1.2.2 工作电压与振荡频率
• 图2.1.1 相移电阻电容网络
• 图2.1.2 不同频率与相位
• 图2.1.3 不同频率与增益
• 图2.2.1 不同的Q1的输入电阻对于振荡频率影响
• 图2.2.2 不同的Q1的输入电阻对于增益的影响
• 图3.1.1 面包板上的搭建的测试电路
• 图3.2.1 Q1集电极以及C1上的电压轨迹
• 图3.2.2 Q1集电极以及C1上的电压轨迹
• 图3.2.3 Q1集电极以及C1上的电压轨迹

#!/usr/local/bin/python
# -*- coding: gbk -*-
#============================================================
# TEST2.PY                     -- by Dr. ZhuoQing 2021-10-03
#
# Note:
#============================================================
from headm import *
P = lambda x,y : x*y/(x+y)
#------------------------------------------------------------
R1 = 5.1e3
R2 = 5.1e3
R3 = 10.0e3
R4 = 10.0e3
rb = 2.7e3
c1 = 0.22e-6
c2 = 0.22e-6
c3 = 0.22e-6
def F(omiga, r=rb, flag=0):
    C1 = 1/(1j * 2 * pi * omiga * c1)
    C2 = 1/(1j * 2 * pi * omiga * c2)
    C3 = 1/(1j * 2 * pi * omiga * c3)
#------------------------------------------------------------
    r1 = R4 + P(C3,r)
    r2 = R3 + P(C2, r1)
    r3 = P(C1, r2)
    Urb_1 = P(C3, rb) / r1
    U1_2 = P(C2, r1) / r2
    U2_c = r3/(R1+R2+r3)
    Fomiga = Urb_1 * U1_2 * U2_c
    if flag > 0:
        printff(abs(Urb_1), abs(U1_2), abs(U2_c), abs(Fomiga))
    return Fomiga
#------------------------------------------------------------
def rb_arg(r):
    fdim = linspace(0.01, 500, 1000)
    fabs = [abs(F(o,r)) for o in fdim]
    fangle = [angle(F(o,r))*180/pi for o in fdim]
    fid = [(lambda x: 0 if x < 100 else 1)(abs(a-b)) for a,b in zip(fangle[:-1], fangle[1:])].index(1)
    freq180 = fdim[fid]
    angle180 = angle(F(freq180, r))*180/pi
    abs180 = abs(F(freq180, r))
    return freq180, angle180, abs180
#------------------------------------------------------------
rbdim = linspace(100, 5000, 100)
fdim = []
adim = []
gdim = []
for r in rbdim:
    f, a, g = rb_arg(r)
    fdim.append(f)
    adim.append(a)
    gdim.append(g)
plt.plot(rbdim, gdim)
plt.xlabel("rb(ohm)")
plt.ylabel("Gain")
plt.grid(True)
plt.tight_layout()
plt.show()
#------------------------------------------------------------
#------------------------------------------------------------
'''
plt.plot(fangle)
plt.xlabel("n")
plt.ylabel("delta")
plt.grid(True)
plt.tight_layout()
plt.show()
'''
#------------------------------------------------------------
'''
plt.plot(fdim, fangle)
plt.xlabel("Frequency(Hz)")
plt.ylabel("Gain")
plt.grid(True)
plt.tight_layout()
plt.show()
'''
#------------------------------------------------------------
printf('\\a')
#------------------------------------------------------------
#        END OF FILE : TEST2.PY
#============================================================