京东物流-三维装箱(记录)
Posted _WILLPOWER_
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了京东物流-三维装箱(记录)相关的知识,希望对你有一定的参考价值。
前言
就只水了个初赛,复赛必须要用Java写,就放弃了,这里记录一下写的东西。
队友:
思禾
OuJiang2021
背景
随着国民经济的快速发展,我国物流行业的业务需求量越来越多。如图1-1所示,根据国家统计局官方数据表明,2016-2021上半年全国社会物流总费用都呈现了增长的趋势,这即是国家国力提升,国民生活素质的不断提高的表现,同时也体现了中国的物流业发展的日益强大。今天的中国的物流业已经建立起世界领先的快递物流体系,与以往科技含量较低的行业状况相比,目前物流行业信息化程度增强,物流集成化和自动化水平有较大提升,但是在对物品进行装箱打包的问题有的企业还是在采用凭借人工方式进行装车配送,由于订单数量的庞大和时限要求,操作人员都是凭借以往经验进行装载,难以保证配送车辆的满载,同时人工装载劳动强度大,装载过程耗费时间长,货物被反复取出装载的现象较为普遍,容易造成货物的破损,进一步增加企业成本。因此在包裹的打包环节,选取合适的包装耗材非常重要。在庞大的包裹基数下,单个包裹耗材成本的略微降低,能带来极大的经济效益和社会效益。

装箱问题可追溯到 1831 年高斯研究布局问题,属于复杂组合优化问题,是 NPC 问题。在 1980 年前,多数研究针对一维、二维装箱问题,1980年后,随着低维装箱问题研究成果积累和计算机技术发展,三维装箱问题逐渐成为学术界热门方向。三维装箱问题在物资装载、物流等行业都有应用。
研究三维装箱问题,能够提高车辆运输的效率,减少车辆的浪费,降低物流的成本,如果在此基础上实现自动化装箱将大大减少企业物流的成本,提升企业的盈利能力,同时其能够减少物流垃圾的产生,减少污染物的排放,因此对三维装箱问题的研究具有十分重要的经济价值。
方法
问题分析
问题一:
根据题目我们需要在提供的订单数据中选择合适的耗材去做出合适的装配方案,并且目标是要用的耗材数量越少,并且耗材的大小越小越好。
这里就牵涉到二个必须考虑的问题:
1、 选择多大的箱子来装物品
2、 物品应该如何放入箱子
问题二:
问题二需要自己给出10种优化的耗材尺寸,要解决这个问题,我们就必须要根据所有订单,给出合适的耗材尺寸,让在物品装箱的时候能够有更大的空间利用率;针对此题,我们考虑了两种方法:
第一个方法就是将在第一题装完一个箱子后,将最终整个箱子的实物品空间坐标得到,然后在得到所有1000个订单的数据后,将1000组数据的体积给求出,由小到大排列,然后分为10组,每组100个数据,在每组中将长宽高分别想加求平均,得到10组长宽高,这样得出10个箱子的优化尺寸;
方法概述
第一版本
为了快速将题给过一遍,我们先没有考虑到袋子的使用,因为袋子的可变换性很强,一开始考虑到袋子的使用会让整个程序显得复杂,会拖慢整个做题的进度,因此我们首先考虑的是直接用箱子,并且在选择箱子的时候,我们暂时选择的是最大的箱子。那么选箱子的问题我们就暂时不考虑,就专注于如何将物品放入箱子,对于这个问题,我们是暂时不考虑物品的旋转问题,按照常规的堆叠操作现将整个流程过一遍,这里采用的是将物品按照y->x->z的顺序,依次放入物品。先朝着y轴放置物品,当y轴上物品y坐标大于箱子的y坐标的时候,那么物品向x轴进行拓展,然后物品再次向y轴拓展,一直到当x轴上物品x坐标大于箱子的x坐标的时候,这个时候又向z轴进行拓展,直至将一个订单中的物品全部装入箱子即可。
第二版本
在能够正常进行工作后,我们在第一版baseline的基础上,加了装箱策略。在进行装配之前,我们首先将所有的箱子的体积算出,然后将箱子的体积由小到大进行排序。然后在拿到一个订单后,我们首先将所有物品的体积算出求和,然后在箱子集合中,拿到体积大于所有物品体积之和的箱子集合2,在箱子集合2中从小到大拿出箱子来装一个订单的所有物品,当拿出的箱子不能够装下的时候就在箱子集合2中拿出下一个箱子,直到能够装下所有物品。
第三章 实验结果
装箱结果分析与验证
下面图一是我们在进行装箱后的仿真结果图。
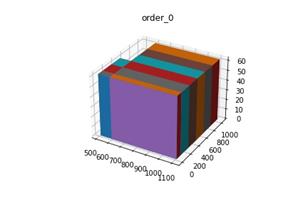
为了更加明确的表明我们的装箱顺序,这里我只拿取了订单0中的数据进行分析,因为后面的装箱步骤和前面没有任何变化,因此,取一个订单进行阐述可能会得到更好的描述结果。
由上图可以看到,我们主要采用的装箱方式为先向y轴进行拓展,直到y轴已经不能拓展位置,这时我们在进行z轴拓展,下图二显示了我们在x方向不够然后向z轴拓展的示意图。
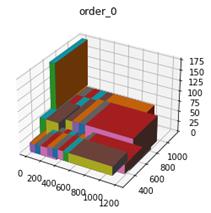
由此,我们依次按照这种y-x-z在y-x-z的顺序向后继续进行,当当前选择的这一个箱子不够用即不能在继续装下任何一个商品时,我们就在拿一个箱子进行装然后按照这种同样的方法进行装,当然若一个箱子能装下所有的SKU那当然最好,下图3显示了一个箱子装满的情况。

上面图三显示了一个箱子将所有当前订单的所有SKU装完的情况,由图三,我们可以看到,该装箱效果还是比较理想,如果箱子选的合理,刚好他的高度方向不能拓展的话,那么该箱子的空间利用率总体来说还是挺大的,其唯一没有利用到的空间就是在进行y向x再向z拓展时,没有选择一个恰好能填补当前轴大小的SKU,但是对于这种空间浪费我们认为在一定条件下是允许的,因为在实际装箱中,我们也不能百分百的的将整个箱子空间利用率占用完,而是只能尽可能大的去利用这个箱子。还有一部分就是在上图3中的顶部,我们直观的这样看过去。感觉上面部分空闲了很大一部分空间,其实实际上并非如此,这里呈现这个原因的主要原因是应为使用的绘图工具为python的matplotlib库进行绘制的,这在绘制的时候,它为了使我们看的更直观,它软件上将z轴正对我们的这一部分给放大了,因此,给我门的感受就像是上部分空闲很大,但实际上,若选箱恰当,它上部分空闲空间只有在想x轴拓展时因为没有SKU而空闲的这一小部分,因此,从整体上来看,我们这样的装箱效果还是蛮理想的。
由上面的仿真结果来看,我们的采取的这种装箱效果满足实际的装箱需求,同时也满足大赛题目要求,并且通过绘图方式,我们可以直观清晰的看到我们的这种装箱方式,结果准确。
总结与展望.
总结
如上所述,本算法主要分为选箱策略、装箱策略、防重叠策略三个部分组成。大体上通过体积计算进行箱子选型,并通过采用体积优先且按照从零点开始放置SKU的方式进行放置,在放置过程中,采用X-Y-Z轴的放置方式进行层次放置策略,且为了保证最大化利用放置空间,预设将相同SKU放置在一起,同时,采用饱和最大一轴的策略来避免SKU放置重叠,即若当前轴放置有多种SKU,那么在迭代到下一轴的放置时,选择当前SKU叠放中最大的下一轴坐标为初始坐标。
本算法生成的装箱结果,获得有效成绩,且由上面的仿真结果来看,我们的采取的这种装箱效果能够满足实际的装箱需求,同时也满足大赛题目要求。
展望
通过本算法虽然能够获得一个较有策略的装箱结果,但从算法步骤和优化策略上看还有较大发展空间:
- 首先在箱子选型中,本算法只考虑了当前单中SKU集体体积这一维度,但是由于体积由SKU长宽高的三个维度共同作用,所以在考虑上还不够全面,后期将会考虑引入一个多方维度(如箱子是否接近SKU长宽高比例等)的衡量函数来对不同箱子对当前单的一个评分再进行选择。
- 在装箱算法上,我们目前按体积最大优先这种贪心策略作为装箱的主要策略,但是缺少了对SKU数量的一个评价,后期可能会尝试引入多个装箱策略,甚至考虑诸如遗传算法,模拟退火算法等组合优化算法来进行放置,甚至会考虑多次回溯的方式来进行对空间的最大利用。
- 在细节处理上,在一轴向另一轴扩展的时候,本算法直接采用饱和最高的坐标点的方式,相对来说有一段空间浪费较大,后期在此处还应该结合SKU三维旋转和重叠面判断的方式进行优化,应该尽量充分利用细隙。
- 在箱体设计上也是本算法后期的一大优化点,在全局上对所有订单的SKU按照前面的优化思路进行装箱之后对于每一个订单应该会有一个较为合适的装箱结果,对所有订单在所用体积以及箱子的长宽高进行数据统计,再尝试以某种策略进行箱体设计。
总之,本算法还有很大的发展空间,对于装箱此类的NP-hard问题,我们只有不断地迭代才能收敛到全局最优,希望后期继续发展,交出更满意地答卷。
代码
#%%
from concurrent.futures import ThreadPoolExecutor
from concurrent.futures import ProcessPoolExecutor
from os import stat, terminal_size
from numpy import string_, zeros
import pandas as pd
import copy
duiwu = '老欧这把能行吧'
xiangzi = '普通京东2号20版平台纸箱'
wenti = '1'
#%%
dingdan = './订单数据.csv'
haocai = './耗材数据.csv'
haocai1 = './缩减耗材数据.csv'
sku = './sku数据.csv'
shili = './用户提交订单数据示例.csv'
data_Dingdan = pd.read_csv(dingdan)
data_Sku = pd.read_csv(sku)
data_Df = pd.read_csv(shili, nrows=0)
#全局变量maxx, maxz为每次拓展的时候要拓展的最大边
maxx = 0
maxz = 0
#%%
#处理箱子,由小到大,并且将耗材的名称作为行的索引
data_Haocai = pd.read_csv(haocai)
data_Haocai1 = pd.read_csv(haocai1)
data_Haocai.set_index(['耗材名称'], inplace=True)
m = []
for i in range(data_Haocai.shape[0]):
m.append(data_Haocai.iloc[i]['长']*data_Haocai.iloc[i]['宽']*data_Haocai.iloc[i]['高'])
data_Haocai['vol'] = m
data_Haocai.sort_values(by='vol', inplace=True)
data_Haocai1.set_index(['耗材名称'], inplace=True)
m = []
for i in range(data_Haocai1.shape[0]):
m.append(data_Haocai1.iloc[i]['长']*data_Haocai1.iloc[i]['宽']*data_Haocai1.iloc[i]['高'])
data_Haocai1['vol'] = m
data_Haocai1.sort_values(by='vol', inplace=True)
#%%
#输入分别为 原点, 箱子长宽高的列表, 物品的长宽高列表
def FitBox(yuandian:list, boxInfo:list, itemInfo:list):
status = True
global maxx
global maxz
#原点+物品大小即判断边界
sum = []
for i in range(len(yuandian)):
sum.append(yuandian[i] + itemInfo[i])
rx, ry, rz = copy.deepcopy(yuandian)
sx, sy, sz = copy.deepcopy(yuandian)
nx, ny, nz = sum
ix, iy, iz = itemInfo
bx, by, bz = boxInfo
#每次进来就是在对y的拓展,因此更新y坐标
ry = ry + iy
#如果拓展后的y比箱子的y大
if(ny > by):
#起始原点向x方向进行拓展,必须是原起始原点x+上一列箱子中X的最大值
sx = sx + maxx
#起始原点拓展后y一定是从0开始
sy = 0
#起始原点更新后,将物品箱子的坐标再次进行计算
nx, ny, nz = sx+ix, sy+iy, sz+iz
#返回原点更新 !起始原点和返回原点是不同的
rx, ry, rz = sx, sy, sz
ry = ry + iy
#每次更新y后,新起一列,因此maxx换
maxx = 0
if(nx > bx):
#这里是判断x方向拓展后比箱子的x大,那么就向上进行拓展,因此和上述差不多,但是原始原点x,y是从0开始了
sz = sz + maxz
sx = 0
sy = 0
nx, ny, nz = sx+ix, sy+iy, sz+iz
rx, ry, rz = sx, sy, sz
ry = ry + iy
#每次更新z后,新起一列,因此maxz换
maxz = 0
#如果拓展z后比箱子大,那么这个箱子失败
if(nz > bz):
status = False
#下面是在向y拓展过程中,要更新这一列放入的箱子中最大的X和Z
if(maxx < ix):
maxx = ix
if(maxz < iz):
maxz = iz
#返回状态,物品起始坐标(返回原点),物品终点坐标,原始坐标
return [status, [rx, ry, rz], [nx, ny, nz],[sx, sy, sz]]
# def Process(df:pd.DataFrame):
def Calc(data_Df:pd.DataFrame, data_Dingdan:pd.DataFrame,
data_Haocai:pd.DataFrame,
wenti:str,duiwu:str ):
template = data_Df.to_dict()
template['问题'] = wenti
template['用户名'] = duiwu
template['包裹号'] = 1
#将每个订单分开
group = data_Dingdan.groupby('订单号')
for i in group:
#拿到一个订单
dingdanNum, dingdanDf = i
template['订单号'] = dingdanNum
#将长宽高以及体积加在订单每个sku的后面,方便使用
d, w, h, s = [], [], [], []
for sku in dingdanDf['SKU编码']:
d.append(data_Sku.iloc[sku]['长'])
w.append(data_Sku.iloc[sku]['宽'])
h.append(data_Sku.iloc[sku]['高'])
s.append(d[-1]*w[-1]*h[-1])
dingdanDf['d'], dingdanDf['w'], dingdanDf['h'], dingdanDf['s'] = d, w, h, s
#根据高排序,让低sku先排
dingdanDf.sort_values(by='h', inplace = True)
#总体积
# itemS = (dingdanDf['数量']*dingdanDf['s']).sum()
#在箱子体积够的从小到大来装
fitboxs = data_Haocai[data_Haocai['vol'] > (dingdanDf['数量']*dingdanDf['s']).sum()]
for b in range(fitboxs.shape[0]):
#箱子名字,以及长宽高的列表
#进行初始化,,进入一次,就是选择一次箱子,初始化原点,耗材名称,模板,状态
boxname, boxInfo = fitboxs.iloc[b].name, fitboxs.iloc[b][1:-1].to_list()
yuandian = [0, 0, 0]
temp = copy.deepcopy(template)
temp['耗材名称'] = boxname
templates = []
status = True
for j in range(dingdanDf.shape[0]):
#取出订单中一行
dingdanRow = dingdanDf.iloc[j]
cntRow = dingdanRow['数量']
temp['SKU'] = dingdanRow['SKU编码']
#物品大小
itemInfo = [dingdanRow['d'], dingdanRow['w'], dingdanRow['h']]
for k in range(cntRow):
status, returnYuanDian, returnZuoBiao, oldYuanDian = FitBox(yuandian, boxInfo, itemInfo)
if(status != False):
#如果成功,更新起点,重点
temp['xStart'],temp['yStart'],temp['zStart'] = oldYuanDian
temp['xEnd'],temp['yEnd'],temp['zEnd'] = returnZuoBiao
#更新原点,注意起点和原点不一样
yuandian = returnYuanDian
templates.append(copy.deepcopy(temp))
else:
# 如果失败退出
break
if(status == False):
#失败退出
break
if(status != False):
#如果没有失败,将得到的装箱信息放入数据
data_Df = data_Df.append(templates, ignore_index=True)
print(data_Df)
break
return(data_Df)
#制造模板
#%%
#保存的时候不取计算物品大小的地方
data_Df1 = Calc(data_Df, data_Dingdan,data_Haocai, wenti, duiwu)
data_Df2 = Calc(data_Df, data_Dingdan,data_Haocai1, '2', duiwu)
data_Df3 =copy.deepcopy(data_Df2)
data_Df3['问题'] = 3
data_Df = data_Df1.append(data_Df2)
data_Df = data_Df.append(data_Df3)
data_Df.to_csv('./老欧这把能行吧-订单数据.csv', index=None, encoding='utf-8')
题目

以上是关于京东物流-三维装箱(记录)的主要内容,如果未能解决你的问题,请参考以下文章
三维装箱基于matlab求解三维装箱优化问题含Matlab源码 1194期