Matlab模拟退火+最低水平线解决物流上的二维装箱问题
Posted 玛丽莲茼蒿
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Matlab模拟退火+最低水平线解决物流上的二维装箱问题相关的知识,希望对你有一定的参考价值。
这里的装箱问题和我们在算法上归纳的装箱问题不是一个概念!也就是不同于下面这篇博客里的装箱问题。
一、二维装箱问题描述
只有一个固定长、宽的箱子。我们有多个不同长、宽的物体。求解是否有一个方案能把物体全部放进去,并且求解最省空间的方法。
二、完整代码
2.1 主程序调用及模拟退火部分
clear
clc %%清空环境变量
%
% 可以读取不同的母板尺寸数据以及待排样矩形件的尺寸数量
%
Yuanliao=[25,21]; %设定母板长度和宽度
BC=xlsread('pakagexls.xls','sheet2'); %读取数据
starttime=cputime;
p=size(BC,1);%size(BC,1)返回矩阵BC的行数,size(BC,2)返回列数
cc=randperm(p); %产生一个初始下料序列
xx=[zeros(p,1)';-ones(p,1)']; %生成一个第一行全 0,第二行全-1 的矩阵后面交换所用
plot([0,Yuanliao(1),Yuanliao(1),0,0],[0;0;Yuanliao(2);Yuanliao(2);0],'--*b'); %绘制原料板
tic;
hold on;
rate0=1;
c0=cc;
x0=xx(1,:);
best=1;
t0=1000; %初始温度
tf=1; %结束温度
dt=0.9;
nk=200; %最大迭代次数 200
% for kk=1:5 %循环 5 次,为了使得到的解真是最优的
tk=t0;
while tk>tf
%%% 进入内循环,内循环 200 次
for k=1:nk
c=cc;
x=xx;
jjj=floor(p*rand+1); % 产生一个邻域是的解
iii=floor(p*rand+1); %%%
kk=floor(p*rand+1);
a=c(iii);
c(iii)=c(jjj);
c(jjj)=a;
x(:,kk)=[x(2,kk);x(1,kk)]; %交换被选中的列的第一行和第二行,从而控制下料的横放竖放
[rate,~]=LOW(BC,c,x(1,:),Yuanliao,0);%调用 LOW 函数进行下料的排序返回剩料率,调用函数中 0 是负责画图的选项0 表示不画图1 表示画图
df=exp(-(rate-rate0)/tk);
if rate>rate0
df=exp(-(rate-rate0)/tk);
if df>rand
cc=c;
xx=x;
rate0=rate;
end
else
cc=c;
xx=x;
rate0=rate;
end
if rate0<best %% 更新历史最优值
best=rate0;
c0=cc;
x0=xx;
end
end
tk=tk*dt;
end
disp('箱子总数p');
p
time=cputime-starttime
toc
% end
[rate,R]=LOW(BC,c0,x0(1,:),Yuanliao,1) %利用求的最优解调用 LOW 函数,输出最优剩料率,R 为最后的水平线。并画图。
注意,箱子(母板)的长宽信息通过代码设置,物体的数据通过excel文件读取。在excel文件中有两列,第一列是长第二列是宽。如下图
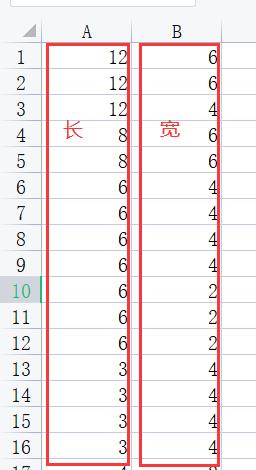
2.2 核心函数部分
function [rate,R]=LOW(BC,c,x,Yuanliao,ifplot)
downloaded_pakage_num=0; %统计放了多少个箱子
p=size(BC,1);
R=[0,0,Yuanliao(1),0];
for i=1:p
if i==1
if x(c(i))==-1
BC(c(i),:)=[BC(c(i),2),BC(c(i),1)];
end
R=[R(1),BC(c(i),2),BC(c(i),1),BC(c(i),2);...
BC(c(i),1),R(2),R(3),R(2)];
S(i,:)=BC(c(i),:);
if ifplot==1
plot([0,S(i,1),S(i,1),0,0],[0,0,S(i,2),S(i,2),0])
hold on;
downloaded_pakage_num=downloaded_pakage_num+1; %!!!!!!!
end
end
if i~=1
if x(i)==-1
BC(c(i),:)=[BC(c(i),2),BC(c(i),1)];
end
k=find(R(:,2)==min(R(:,2)));
[~,k]=sort(R(:,2));
n=size(R,1);
S(i,:)=BC(c(i),:);
for ii=1:size(k,1)
if ((R(k(ii),3)-R(k(ii),1))==BC(c(i),1))&&((Yuanliao(2)- R(k(ii),2))>BC(c(i),2)||(Yuanliao(2)-R(k(ii),2))==BC(c(i),2)) %------------------
R(k(ii),:)=[R(k(ii),1),BC(c(i),2)+R(k(ii),2),BC(c(i),1)+R(k(ii),1),BC(c(i),2)+R(k(ii),2)];
if ifplot==1
plot([R(k(ii),1),R(k(ii),3),R(k(ii),3),R(k(ii),1),R(k(ii),1)],...
[R(k(ii),2)-S(i,2),R(k(ii),2)- S(i,2),R(k(ii),4),R(k(ii),4),R(k(ii),2)-S(i,2)])
hold on;
downloaded_pakage_num=downloaded_pakage_num+1; %!!!!!!!
end
break;
elseif ((R(k(ii),3)-R(k(ii),1))>BC(c(i),1))&&((Yuanliao(2)- R(k(ii),2))>BC(c(i),2)||(Yuanliao(2)-R(k(ii),2))==BC(c(i),2))
R(n+1,:)=[BC(c(i),1)+R(k(ii),1),R(k(ii),2),R(k(ii),3),R(k(ii),4)] ;
R(k(ii),:)=[R(k(ii),1),BC(c(i),2)+R(k(ii),2),BC(c(i),1)+R(k(ii),1),BC(c(i),2)+R(k(ii),2)];
if ifplot==1
plot([R(k(ii),1),R(k(ii),3),R(k(ii),3),R(k(ii),1),R(k(ii),1)],...
[R(k(ii),2)-S(i,2),R(k(ii),2)-S(i,2),R(k(ii),4),R(k(ii),4),R(k(ii),2)-S(i,2)])
hold on;
downloaded_pakage_num=downloaded_pakage_num+1; %!!!!!!!
end
break;
end
if ((R(k(ii),3)-R(k(ii),1))==BC(c(i),2))&&((Yuanliao(2)-R(k(ii),2))>BC(c(i),1)||(Yuanliao(2)-R(k(ii),2))==BC(c(i),1)) %------------------
R(k(ii),:)=[R(k(ii),1),BC(c(i),1)+R(k(ii),2),BC(c(i),2)+R(k(ii),1),BC(c(i),1)+R(k(ii),2)];
if ifplot==1
plot([R(k(ii),1),R(k(ii),3),R(k(ii),3),R(k(ii),1),R(k(ii),1)],...
[R(k(ii),2)-S(i,1),R(k(ii),2)-S(i,1),R(k(ii),4),R(k(ii),4),R(k(ii),2)-S(i,1)])
hold on;
downloaded_pakage_num=downloaded_pakage_num+1; %!!!!!!!
end
break;
elseif ((R(k(ii),3)-R(k(ii),1))>BC(c(i),2))&&((Yuanliao(2)-R(k(ii),2))>BC(c(i),1)||(Yuanliao(2)-R(k(ii),2))==BC(c(i),1))
R(n+1,:)=[BC(c(i),2)+R(k(ii),1),R(k(ii),2),R(k(ii),3),R(k(ii),4)] ;
R(k(ii),:)=[R(k(ii),1),BC(c(i),1)+R(k(ii),2),BC(c(i),2)+R(k(ii),1),BC(c(i),1)+R(k(ii),2)];
if ifplot==1
plot([R(k(ii),1),R(k(ii),3),R(k(ii),3),R(k(ii),1),R(k(ii),1)],...
[R(k(ii),2)-S(i,1),R(k(ii),2)-S(i,1),R(k(ii),4),R(k(ii),4),R(k(ii),2)-S(i,1)])
hold on;
downloaded_pakage_num=downloaded_pakage_num+1; %!!!!!!!
end
break;
end
end
b=unique(R(:,2));
if size(b,1)~=size(R(:,2),1)
for i=1:size(b,1)
t=find(R(:,2)==b(i));
if size(t,1)~=1
for ii=1:size(t,1)-1
if (R(t(ii),3)==R(t(ii+1),1))||(R(t(ii),1)==R(t(ii+1),3))
SS=[min(R(t(ii),1),R(t(ii+1),1)),R(t(ii),2),...
max(R(t(ii),3),R(t(ii+1),3)),R(t(ii),2)];
R(t(ii+1),:)=SS;
R(t(ii),:)=0;
end
end
end
end
end
R(all(R==0,2),:)=[];
end
end
Area=0;
for i=1:size(R,1)
Area=Area+(R(i,3)-R(i,1))*(Yuanliao(2)-R(i,4));
end
rate=Area/(Yuanliao(1)*Yuanliao(2));
downloaded_pakage_num %输出一共放好了多少箱子
2.3 运行结果解析
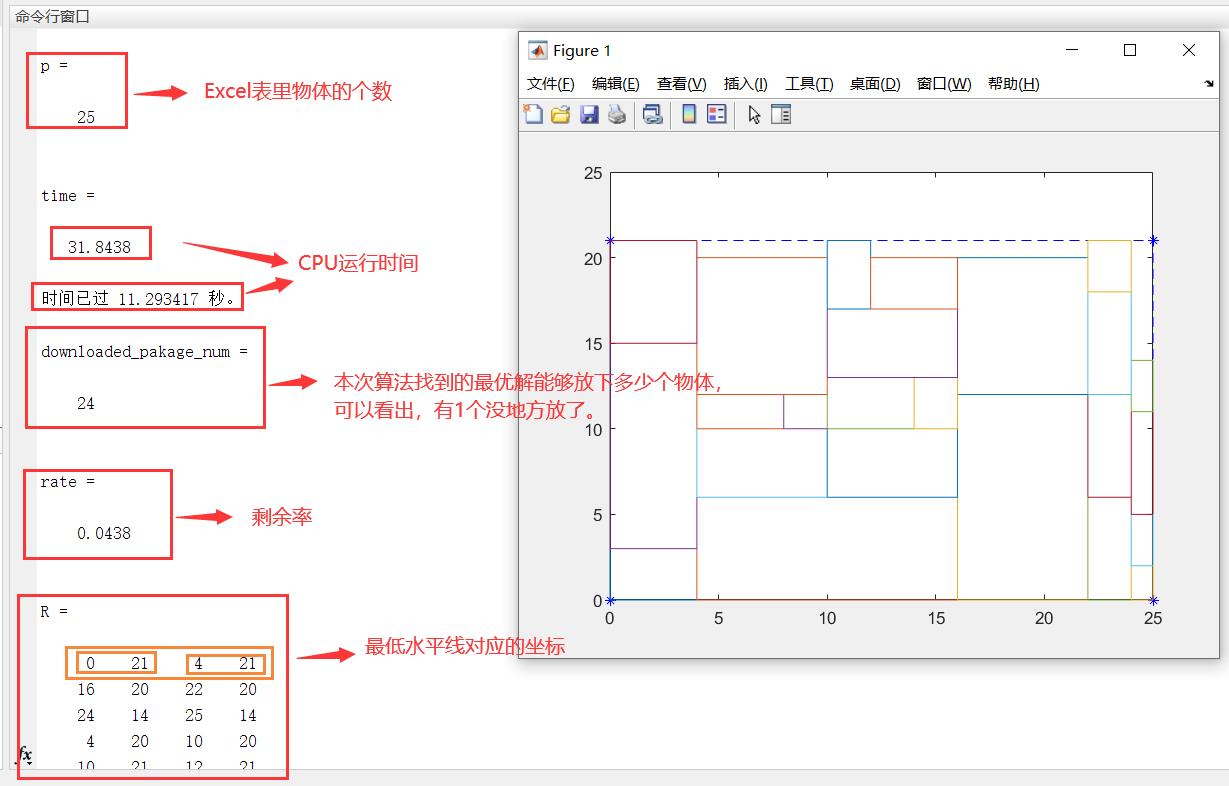
为了方便看懂,对其中某些结果进行解释:
1. 最低水平线。
我们用虚线画出了最低水平线。
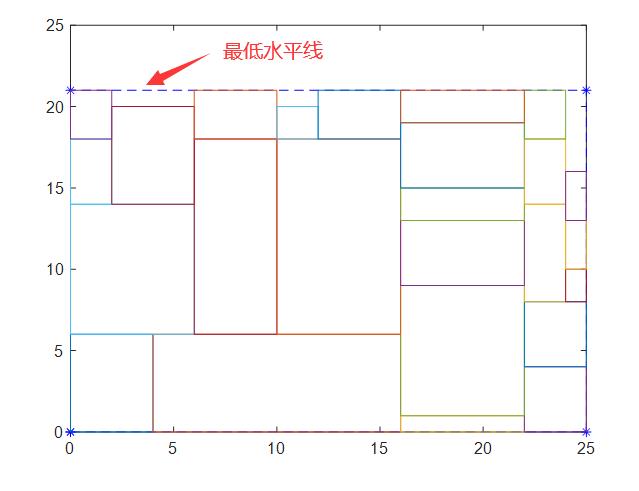
输出的结果R应该是离最低水平线最近的物体的坐标,图中我写的“最低水平线的坐标”是不对的,不想改了。这个R应该一行一行的看,每一行由:x1,y1;x2,y2组成,把(x1,y1)和(x2,y2)连起来便是一条线。
2. 剩余率。
先说容积率,箱子的容积率是所有物体的面积除以箱子最低水平线下的面积。用1减去容积率便是剩余率,越小越好。
3.CPU运行时间
用两种方法给出了CPU运行时间,一般以第二种为准。
以上是关于Matlab模拟退火+最低水平线解决物流上的二维装箱问题的主要内容,如果未能解决你的问题,请参考以下文章
 https://blog.csdn.net/qq_44886213/article/details/124209211?spm=1001.2014.3001.5502
https://blog.csdn.net/qq_44886213/article/details/124209211?spm=1001.2014.3001.5502