龙格库塔法基本C程序

Posted 2021-10-16 bcbobo21cn

数值分析中，龙格－库塔法（Runge-Kutta methods）是用于非线性常微分方程的解的重要的一类隐式或显式迭代法。
龙格-库塔(Runge-Kutta)方法是一种在工程上应用广泛的高精度单步算法，其中包括著名的欧拉法，用于数值求解微分方程。由于此算法精度高，采取措施对误差进行抑制，所以其实现原理也较复杂。

    我还不了解什么是高精度单步算法，只知道是用来求微分方程数值解的；

对于Matlab的Simulink的解法器有如下描述；

    解法器
    针对变步长和定步长分别有不同的解法器。
    变步长模式解法器有：ode45，ode23，ode113，ode15s，ode23s，ode23t，ode23tb和discrete。
    1）ode45：缺省值，四/五阶龙格－库塔法，适用于大多数连续或离散系统，但不适用于刚性（stiff）系统。它是单步解法器，也就是，在计算y(tn)时，它仅需要最近处理时刻的结果y(tn-1)。一般来说，面对一个仿真问题最好是首先试试ode45；
    2）ode23：二/三阶龙格－库塔法，它在误差限要求不高和求解的问题不太难的情况下，可能会比ode45更有效。也是一个单步解法器；

    。。。。。。

    我还不太了解什么是解法器；

下面来看一下龙格库塔基本C程序；VC6.0版本；

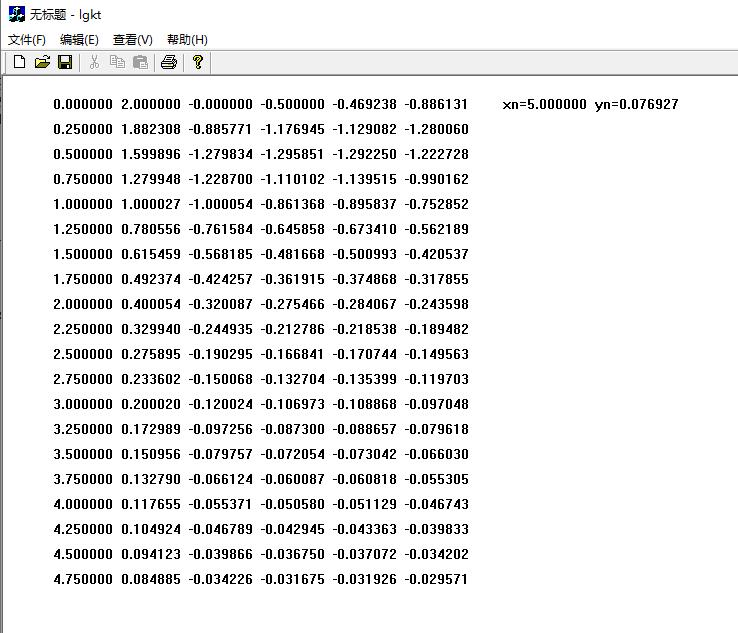
输出如下；我还不理解此程序；

 

代码；

void CLgktView::OnDraw(CDC* pDC)
{
	CLgktDoc* pDoc = GetDocument();
	ASSERT_VALID(pDoc);
	// TODO: add draw code for native data here
	double a,b,x0,y0,k1,k2,k3,k4,h;
	int n,i;
    a=0;
	b=5;
	x0=0;
	y0=2;
	n=20;
	CString str1, str2;
	int row=0;

	for(h=(b-a)/n,i=0;i!=n;i++)
	{
		k1=f(x0,y0);
		k2=f(x0+h/2,y0+k1*h/2);
		k3=f(x0+h/2,y0+k2*h/2);
		k4=f(x0+h,y0+h*k3);
		str1.Format("%lf  %lf  %lf  %lf  %lf  %lf",x0,y0,k1,k2,k3,k4);
		pDC->TextOut(50,20+row*25,str1);
		y0+=h*(k1+2*k2+2*k3+k4)/6;
		x0+=h;
		row=row+1;
	}
	str2.Format("xn=%lf  yn=%lf", x0, y0);
	pDC->TextOut(500,20,str2);
}