C/C++数据结构-完整代码队列Queue（树和二叉树）（二叉树代码实现）

Posted 2021-10-15 蓝盒子itbluebox

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了C/C++数据结构-完整代码队列Queue（树和二叉树）（二叉树代码实现）相关的知识，希望对你有一定的参考价值。

一、树的基本概念

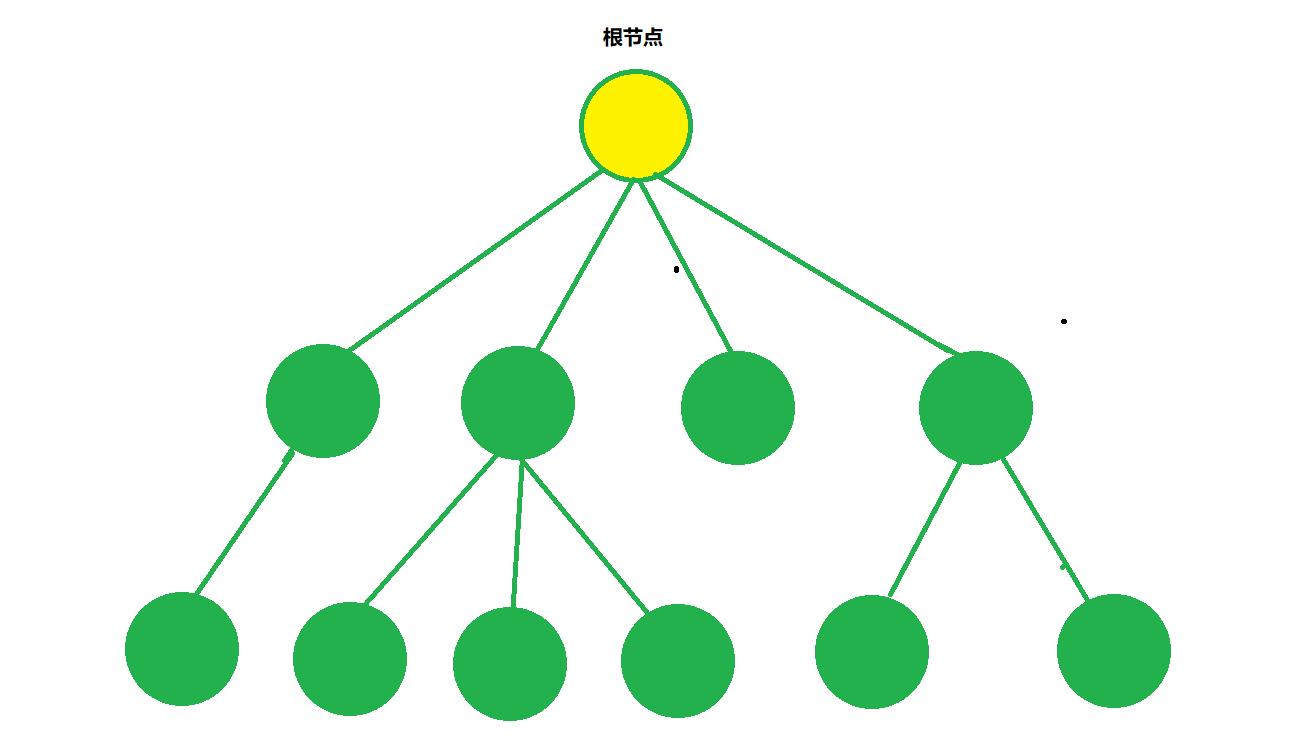
1、树的定义

由一个或多个(n≥0)结点组成的有限集合T ,

有且仅有一个结点称为根( root ) ,

当n>1时，

其余的结点分为m(m≥0)个互不相交的有限集合T1,T2,…，Tm。

每个集合本身又是棵树，被称作这个根的子树。

2、树的结构特点

非线性结构，有一个直接前驱，但可能有多个直接后继( 1:n )
树的定义具有递归性，树中还有树。
树可以为空，即节点个数为0。

3、若干术语

根→即根结点(没有前驱)
叶子→即终端结点(没有后继)
森林→指m棵不相交的树的集合(例如删除A后的子树个数)
有序树→结点各子树从左至右有序，不能互换(左为第一)
无序树→结点各子树可互换位置。
双亲→即上层的那个结点(直接前驱) parent
孩子→即下层结点的子树(直接后继)child-
兄弟→同一双亲下的同层结点(孩子之间互称兄弟) siblinge
堂兄弟→即双亲位于同一层的结点(但并非同一双亲) cousin
祖先→即从根到该结点所经分支的所有结点
子孙→即该结点下层子树中的任一结点
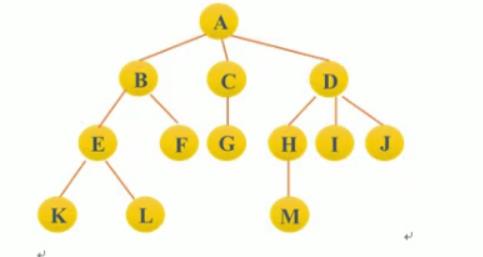
结点→即树的数据元素
结点的度→结点挂接的子树数(有几个直接后继就是几度）
结点的层次→从根到该结点的层数（根结点算第一层)
终端结点→即度为0的结点，即叶子
分支结点→除树根以外的结点（也称为内部结点)
树的度→所有结点度中的最大值( Max{各结点的度})
树的深度(或高度)→指所有结点中最大的层数(Max{各结点的层次})

上图中的结点数 = 13 ，树的度 = 3 ，数的深度 = 4

二、树的表示法

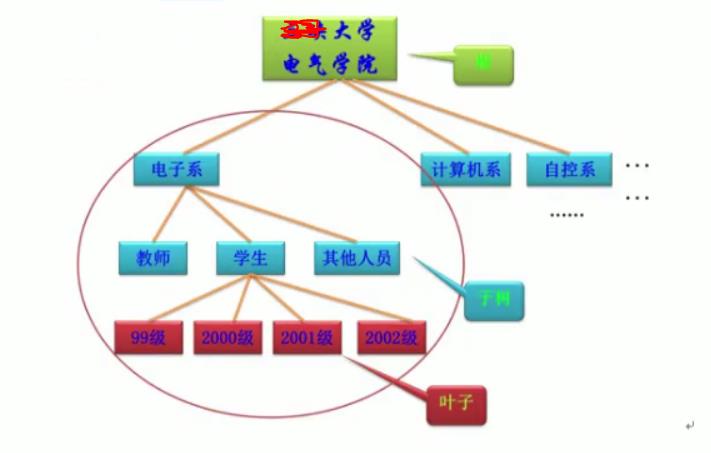
1、图形表示法

事物之问的逻辑关系可以通过数的形式很直观的表示出来，如下图:

2、广义表示法

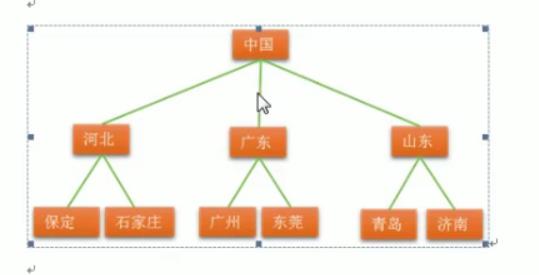
用广义表表示法表示上图:

中国(河北(保定，石家庄),广东(广州，东莞),山东（青岛，济南))

根作为由子树森林组成的表的名宁写在表的左边。

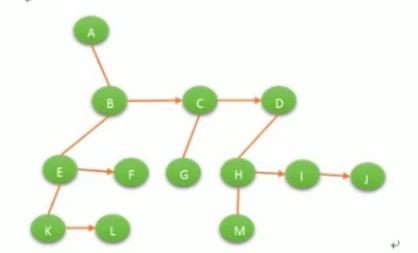
3、左孩子右兄弟表示法

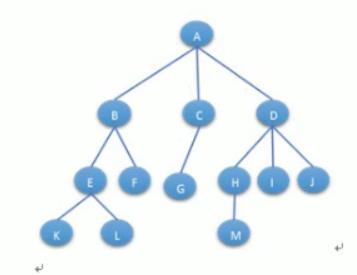
左孩子右兄弟表示法可以将一颗多叉树转化为一颖二叉树:

三、二叉树的概念

1、二叉树的基本概念

（1）定义：

n ( n≥0 )个结点的有限集合，由一个根结点以及两棵互不相交的、分别称为左子树和
右子树的二叉树组成。

（2）逻辑结构：

一对二（1:2）

（3）基本特性

每个结点最多只有两棵子树(丕存在度大于2的结点);

左子树和右子树次序不能颠倒(有序树)

（4）基本形态

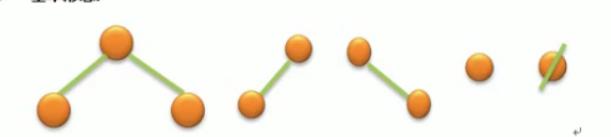
2、二叉树的性质

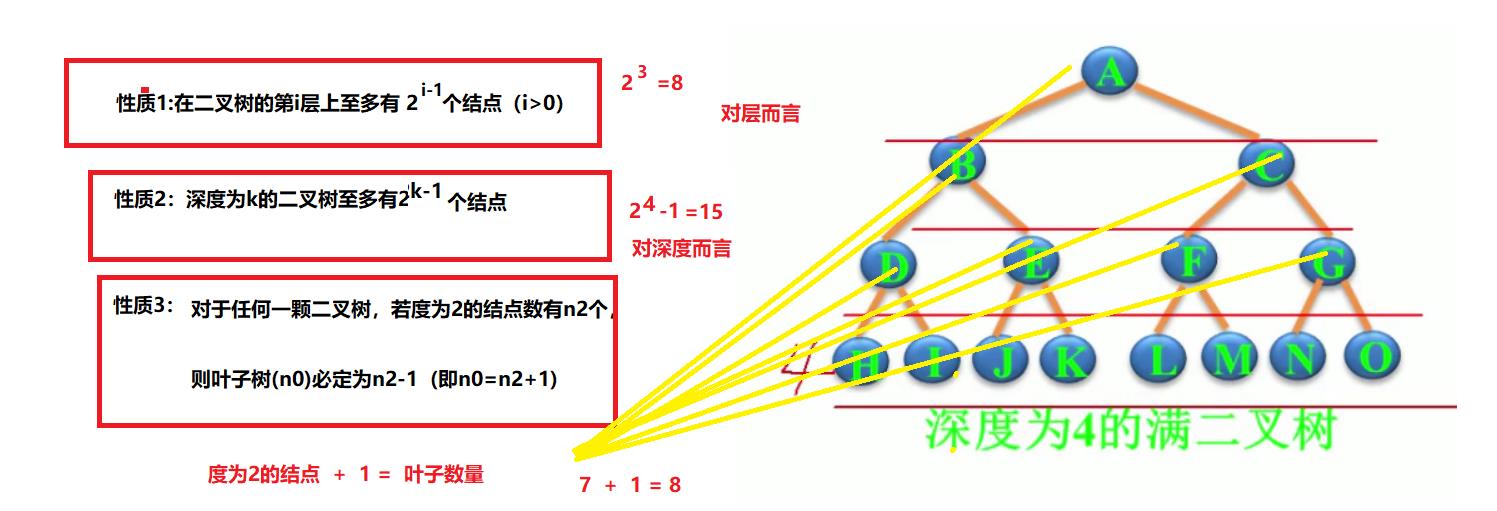
3、满二叉树

特点：每层都有”充满”了结点

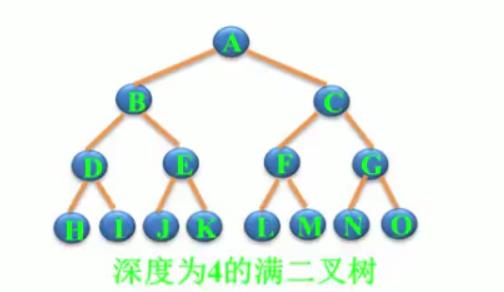
4、完全二叉树

除最后一层外，每一层上的节点均达到最大值；在最后一层上只缺少右边的若干结点

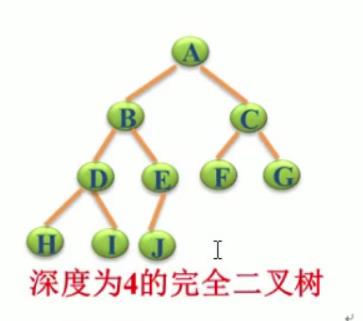
理解：k-1层与满二叉树完全相同，第k层结点尽量靠左

（1）性质4：具有n个结点的完全二叉树的深度必为

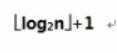
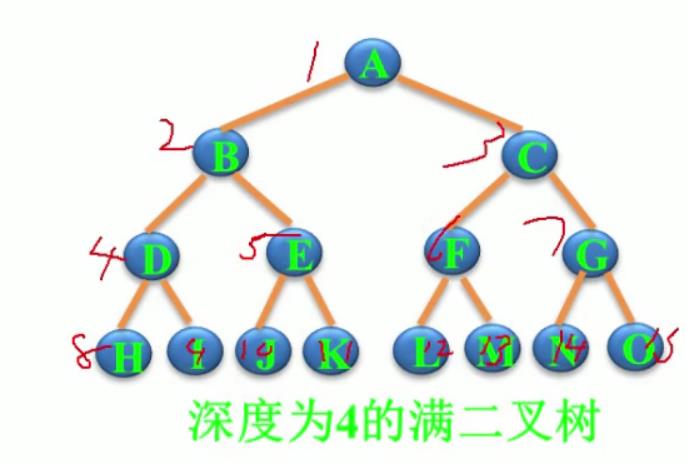
（2）性质5：对完全二叉树，若从上到下，从左到右编号，则编号为i的结点，其左孩子编号为2i，其右孩子编号必为2i+1 ,其双亲的编号必为i/2（i=1时为根除外）

四、二叉树编程

1、二叉树的遍历

（1）遍历定义

指按某条搜索路线遍访每个结点且不重复(又称周游入

（2）遍历用途

它是树结构插入、删除、修改、查找和排序运算的前提，是二叉树一切运算的基础和核
心。

（3）遍历方法

牢记一种约定，对每个结点的查看都是“先左后右”。
限定先左后右，树的遍历有三种实现方案∶

DLR一先序遍历，即先根再左再右
LDR一中序遍历，即先左再根再右
LRD一后序遍历，即先左再右再根

注:"先、中、后”的意思是指访问的结点D是先于子树出现还是后于子树出现。

从递归的角度看，这三种算法是完全相同的，

或者说这三种遍历算法的访问路径是相同的，

只是访问结点的时机不同。

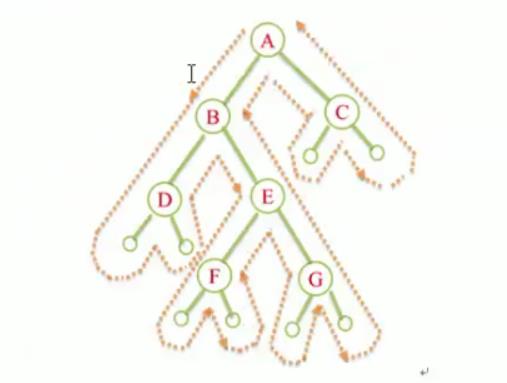
从虚线的出发点到终点的路径上，每个结点经过3次。

第1次经过时访问=先序遍历
第2次经过时访问=中序遍历
第3次经过时访问=后序遍历

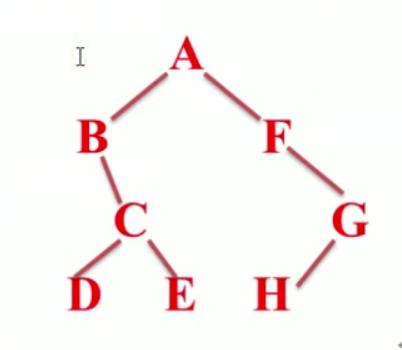
先序遍历：根左右

中序遍历：左根右

后续遍历：左右根

2、二叉树的遍历（代码实现）

（1）先序变量

#include <stdio.h>
#include "string.h"
#include "stdlib.h"
struct BinaryNode{
    char ch;//数据域
    struct BinaryNode * LChild;//左孩子节点
    struct BinaryNode * RChild;//右孩子节点
};
//递归遍历的函数
void recursion(struct BinaryNode * root){
    if(root == NULL){
        return;
    }
    //先序遍历，先根  再左  再右
    printf ("%c ",root->ch);
    recursion (root->LChild);
    recursion (root->RChild);
}

void test01(){

    struct BinaryNode nodeA = {'A',NULL,NULL};
    struct BinaryNode nodeB = {'B',NULL,NULL};
    struct BinaryNode nodeC = {'C',NULL,NULL};
    struct BinaryNode nodeD = {'D',NULL,NULL};
    struct BinaryNode nodeE = {'E',NULL,NULL};
    struct BinaryNode nodeF = {'F',NULL,NULL};
    struct BinaryNode nodeG = {'G',NULL,NULL};
    struct BinaryNode nodeH = {'H',NULL,NULL};

    //建立结点之间的关系

    nodeA.LChild = &nodeB;
    nodeA.RChild = &nodeF;

    nodeB.RChild = &nodeC;

    nodeC.LChild = &nodeD;
    nodeC.RChild = &nodeE;

    nodeF.RChild = &nodeG;
    nodeG.LChild = &nodeH;
    
    //递归遍历
    recursion(&nodeA);
}

int main () {
    test01();
    return 0;
}

运行结果

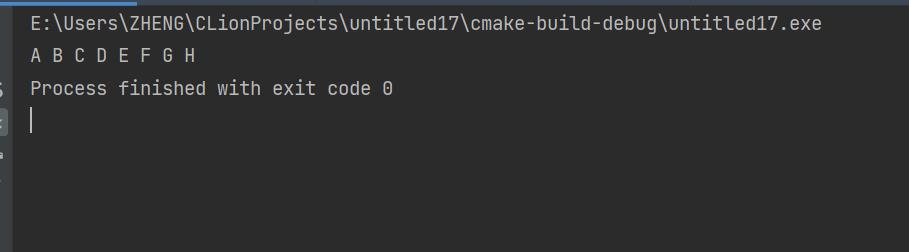
（2）下面代码依次实现中序和后序遍历代码

#include <stdio.h>
#include "string.h"
#include "stdlib.h"
struct BinaryNode{
    char ch;//数据域
    struct BinaryNode * LChild;//左孩子节点
    struct BinaryNode * RChild;//右孩子节点
};
//递归遍历的函数
void preorderRecursion(struct BinaryNode * root){
    if(root == NULL){
        return;
    }
    //先序遍历，先根  再左  再右
    printf ("%c ",root->ch);
    preorderRecursion (root->LChild);
    preorderRecursion (root->RChild);
}
//递归遍历的函数
void inRecursion(struct BinaryNode * root){
    if(root == NULL){
        return;
    }
    //中序遍历，先根  再左  再右
    inRecursion (root->LChild);
	 printf ("%c ",root->ch);
    inRecursion (root->RChild);
}
//递归遍历的函数
void afterRecursion(struct BinaryNode * root){
    if(root == NULL){
        return;
    }
    //中序遍历，先根  再左  再右
    afterRecursion (root->LChild);
    afterRecursion (root->RChild);
	printf ("%c ",root->ch);
}
void test01(){

    struct BinaryNode nodeA = {'A',NULL,NULL};
    struct BinaryNode nodeB = {'B',NULL,NULL};
    struct BinaryNode nodeC = {'C',NULL,NULL};
    struct BinaryNode nodeD = {'D',NULL,NULL};
    struct BinaryNode nodeE = {'E',NULL,NULL};
    struct BinaryNode nodeF = {'F',NULL,NULL};
    struct BinaryNode nodeG = {'G',NULL,NULL};
    struct BinaryNode nodeH = {'H',NULL,NULL};

    //建立结点之间的关系

    nodeA.LChild = &nodeB;
    nodeA.RChild = &nodeF;

    nodeB.RChild = &nodeC;

    nodeC.LChild = &nodeD;
    nodeC.RChild = &nodeE;

    nodeF.RChild = &nodeG;
    nodeG.LChild = &nodeH;
    
    //递归遍历
	
	printf("先序遍历\\n");
    preorderRecursion(&nodeA);
	printf("\\n中序遍历\\n");
	inRecursion(&nodeA);
	printf("\\n后序遍历\\n");
	afterRecursion(&nodeA);
}

int main () {
    test01();
    return 0;
}

运行结果

3、计算二叉树的叶子结点

#include <stdio.h>
#include "string.h"
#include "stdlib.h"
struct BinaryNode{
    char ch;//数据域
    struct BinaryNode * LChild;//左孩子节点
    struct BinaryNode * RChild;//右孩子节点
};
//统计叶子数量的函数
void calculateLeafNum(struct BinaryNode * root, int * num){

    //递归的结束条件
    if(root == NULL){
        return;
    }
    //判断当前节点的左孩子和右孩子是否为空。如果为空数字就累加
    if(root->LChild == NULL && root->RChild == NULL){
        (*num)++;
    }
    calculateLeafNum (root->LChild,num);
    calculateLeafNum (root->RChild,num);


}

void test01(){

    struct BinaryNode nodeA = {'A',NULL,NULL};
    struct BinaryNode nodeB = {'B',NULL,NULL};
    struct BinaryNode nodeC = {'C',NULL,NULL};
    struct BinaryNode nodeD = {'D',NULL,NULL};
    struct BinaryNode nodeE = {'E',NULL,NULL};
    struct BinaryNode nodeF = {'F',NULL,NULL};
    struct BinaryNode nodeG = {'G',NULL,NULL};
    struct BinaryNode nodeH = {'H',NULL,NULL};

    //建立结点之间的关系

    nodeA.LChild = &nodeB;
    nodeA.RChild = &nodeF;

    nodeB.RChild = &nodeC;

    nodeC.LChild = &nodeD;
    nodeC.RChild = &nodeE;

    nodeF.RChild = &nodeG;
    nodeG.LChild = &nodeH;

    //求树中的叶子的数量
    int num = 0;
    calculateLeafNum(&nodeA ,&num);
    printf ("LeafNum=%d",num);

}

int main () {
    test01();
    return 0;
}

4、计算树的深度/高度

int getTreeHeight(struct BinaryNode* root){
    if(root == NULL){
        return  0;
    }
    //求出左子树的高度
    int LHeight = getTreeHeight(root->LChild);
    //计算右子树的高度
    int RHeight = getTreeHeight(root->RChild);

    //取左子树和右子树，中最大的值 +1
    int height = LHeight > RHeight ? LHeight + 1 : RHeight + 1;

    return height;

}

计算相关的所有代码

#include <stdio.h>
struct BinaryNode{
    char ch;//数据域
    struct BinaryNode * LChild;//左孩子节点
    struct BinaryNode * RChild;//右孩子节点
};
//统计叶子数量的函数
void calculateLeafNum(struct BinaryNode * root, int * num){

    //递归的结束条件
    if(root == NULL){
        return;
    }
    //判断当前节点的左孩子和右孩子是否为空。如果为空数字就累加
    if(root->LChild == NULL && root->RChild == NULL){
        (*num)++;
    }
    calculateLeafNum (root->LChild,num);
    calculateLeafNum (root->RChild,num);
}

int getTreeHeight(struct BinaryNode* root){
    if(root == NULL){
        return  0;
    }
    //求出左子树的高度
    int LHeight = getTreeHeight(root->LChild);
    //计算右子树的高度
    int RHeight = getTreeHeight(root->RChild);
    //取左子树和右子树，中最大的值 +1
    int height = LHeight > RHeight ? LHeight + 1 : RHeight + 1;
    return height;
}

void test01(){
    struct BinaryNode nodeA = {'A',NULL,NULL};
    struct BinaryNode nodeB = {'B',NULL,NULL};
    struct BinaryNode nodeC = {'C',NULL,NULL};
    struct BinaryNode nodeD = {'D',NULL,NULL};
    struct BinaryNode nodeE = {'E',NULL,NULL};
    struct BinaryNode nodeF = {'F',NULL,NULL};
    struct BinaryNode nodeG = {'G',NULL,NULL};
    struct BinaryNode nodeH = {'H',NULL,NULL};
    //建立结点之间的关系
    nodeA.LChild = &nodeB;
    nodeA.RChild = &nodeF;

    nodeB.RChild = &nodeC;

    nodeC.LChild = &nodeD;
    nodeC.RChild = &nodeE;

    nodeF.RChild = &nodeG;
    nodeG.LChild = &nodeH;

    //1、求树中的叶子的数量
    int num = 0;
    calculateLeafNum(&nodeA ,&num);
    printf ("LeafNum=%d\\n",num);

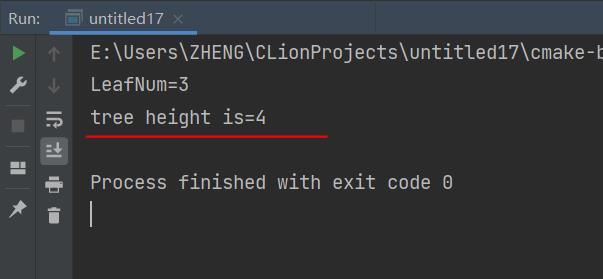
    //2、求树的高度、深度
    int height = getTreeHeight(&nodeA);

    printf ("tree height is=%d\\n",height);
}

int main () {
    test01();
    return 0;
}

5、二叉树的拷贝

struct BinaryNode *  copyBinaryTree(struct BinaryNode* root){

    if(root == NULL){
        return NULL;
    }
    //先拷贝 左子树
    struct BinaryNode * LChild = copyBinaryTree (root->LChild);
    //再拷贝 右子树
    struct BinaryNode * RChild = copyBinaryTree (root->RChild);
    //创建新的节点
    struct BinaryNode * newNode = malloc(sizeof (struct BinaryNode ));
    newNode->LChild = LChild;
    newNode->RChild = RChild;
    //返回给新用户
    newNode->ch = root->ch;
    return newNode;

}

//遍历树
void showBinaryTree(struct BinaryNode * root){

    if(root == NULL){
        return;
    }
    printf ("%c",root->ch);
    showBinaryTree C/C++数据结构-完整代码队列Queue（顺序存储，链式存储）增删改查
 C/C++数据结构-完整代码队列Queue（顺序存储，链式存储）增删改查
 树和二叉树
 5.5树和二叉树——二叉树的层次遍历算法
 树和二叉树的概念
 期末复习笔记——树和二叉树