第2章 逻辑代数基础

Posted 2021-10-15 可能自洽

第2章 逻辑代数基础

一、逻辑代数中的三种基本运算

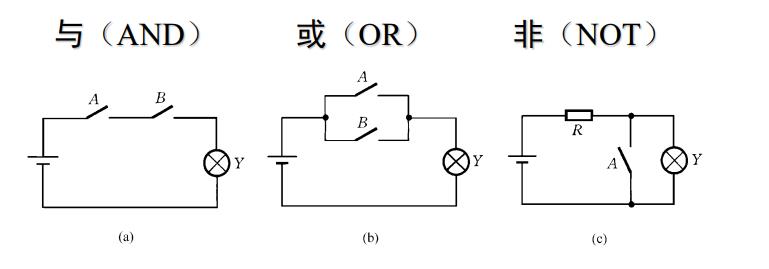
二、逻辑代数的公式

1.基本公式

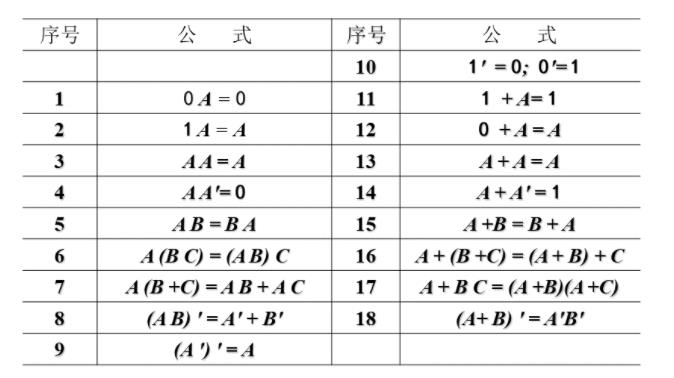
2.常用公式

$A+AB=A$
$A+A^{\prime }B=(A+A^{\prime })(A+B)=A+B$
$AB+A^{\prime }C+BC=AB+A^{\prime }C+(A+A^{\prime })BC=AB+A^{\prime }C$

三、逻辑代数的基本定理

1.反演定理

对任一逻辑式求反
变换顺序： 先括号，然后“乘”，最后“加”
注意事项：不属于单个变量上的反号保留不变

例

1) $Y=A{B}^{\prime }+A^{\prime }B+C$

$Y^{\prime }=\left(A^{\prime }+B\right)\left(A+B^{\prime }\right)C^{\prime }$

2) $Y={\left({\left(A{B}^{\prime }+C\right)}^{\prime }+D\right)}^{\prime }+C$

$Y^{\prime }={\left({\left(\left(A^{\prime }+B\right)C^{\prime }\right)}^{\prime }{D}^{\prime }\right)}^{\prime }{C}^{\prime }$

3) $Y=A(B+C)+CD$

$Y^{\prime }=(A^{\prime }+B^{\prime }{C}^{\prime })(C^{\prime }+D^{\prime })=A^{\prime }{C}^{\prime }+B^{\prime }{C}^{\prime }+A^{\prime }{D}^{\prime }+B^{\prime }{C}^{\prime }{D}^{\prime }=A^{\prime }{C}^{\prime }+B^{\prime }{C}^{\prime }+A^{\prime }{D}^{\prime }$

2.对偶定理

$对偶式：Y^D$
$\bullet \Rightarrow +,+\Rightarrow \bullet ,0\Rightarrow 1,1\Rightarrow 0$

例

$Y=A(B+C),则{\mathrm{Y}}^D=A+BC$
$Y=AB+(C+D{)}^{\prime },则Y^D=(A+B)(CD{)}^{\prime }$

四、逻辑函数

1.表示形式

1.1 真值表

1.2 逻辑表达式

将输入/输出之间的逻辑关系用与/或/非的运算式表示出来

例 写出下面逻辑问题的逻辑表达式和真值表

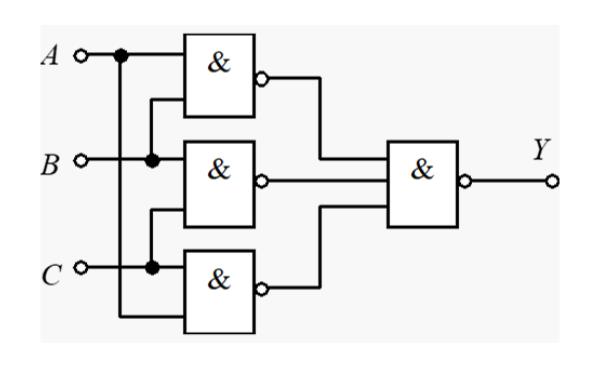
$Y=AB+BC+AC$

1.3 逻辑图

1.4 波形图

1.5 卡诺图

2.逻辑函数表达式的标准形式

2.1 最小项

在一个逻辑函数中，包含全部变量的乘积项称为最小项。( 全部变量以原变量或反变量的形式在乘积项中出现且仅出现一次)

(1) 性质

性质1:在输入变量的任何取值下必有一个且仅有一个最小项的值为1;
性质2:全体最小项之和为‘1’
性质3:任意两个最小项的乘积为‘0’
性质4:具有相邻性的两个最小项之和可以合并成一项并消去一对因子。

(2) 最小项标准表达式

由最小项组成的与或逻辑表达式，称为标准与或表达式，也称为最小项标准表达式。
F = A ′ C + A B ′ = A ′ C ( B + B ′ ) + A B ′ ( C + C ′ ) = A ′ B C + A ′ B ′ C + A B ′ C + A B ′ C ′ = m 3 + m 1 + m 5 + m 4 = ∑ m ( 1 , 3 , 4 , 5 ) \\begin{aligned} F &=A'C+A B' \\\\ &=A'C\\left(B+B'\\right)+A B'\\left(C+C'\\right) \\\\ &=A'BC+A'B'C+AB'C+AB'C' \\\\ &=m_{3}+m_{1}+m_{5}+m_{4} \\\\ &=\\sum m(1,3,4,5) \\end{aligned} F以上是关于第2章 逻辑代数基础的主要内容，如果未能解决你的问题，请参考以下文章

数字电路逻辑设计笔记:逻辑代数基础

高等代数(第四版) 王萼芳课后答案

数字电路再学习之逻辑代数基础

数字逻辑电路（二逻辑代数基础）

20191320《信息安全导论》第四周学习总结

逻辑代数基础（部分）