数字电路逻辑设计笔记:逻辑代数基础
Posted 临风而眠
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数字电路逻辑设计笔记:逻辑代数基础相关的知识,希望对你有一定的参考价值。
数字电路逻辑设计笔记(2):逻辑代数基础
参考教材:《数字电路逻辑设计》欧阳星明 人民邮电出版社
文章目录
§2.1 逻辑代数基础
一.逻辑代数的基本概念
1.逻辑代数
逻辑代数,是英国数学家乔治布尔(Geroge Boole)于1847年首先进行系统论述的,也称布尔代数;后来,美国数学家香农将布尔代数应用于开关矩阵电路中,故又称为开关代数
逻辑变量
逻辑代数中的变量称为逻辑变量,用字母表示
逻辑变量的取值只有逻辑0和逻辑1两种
因此逻辑代数也称为二值代数
逻辑运算
- 两个表示不同逻辑状态的二进制数码之间按照某种因果关系进行的运算
功能描述方法
真值表
- 将输入变量的所有取值组合所对应的输出变量的值全部列出来形成的表格
理论地位:
现实中逻辑命题转化为数字化逻辑描述的桥梁
定义
逻辑真值表,简称真值表,是一种用于描述逻辑函数的全部真伪关系的表格
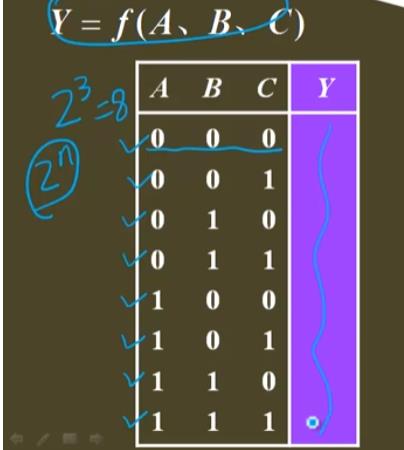
如:三输入一输出逻辑函数对应的真值表
按照二进制数递增顺序排列可以防止漏掉状态
例子

总结

逻辑符号
-
用规定的图形符号来表示
-
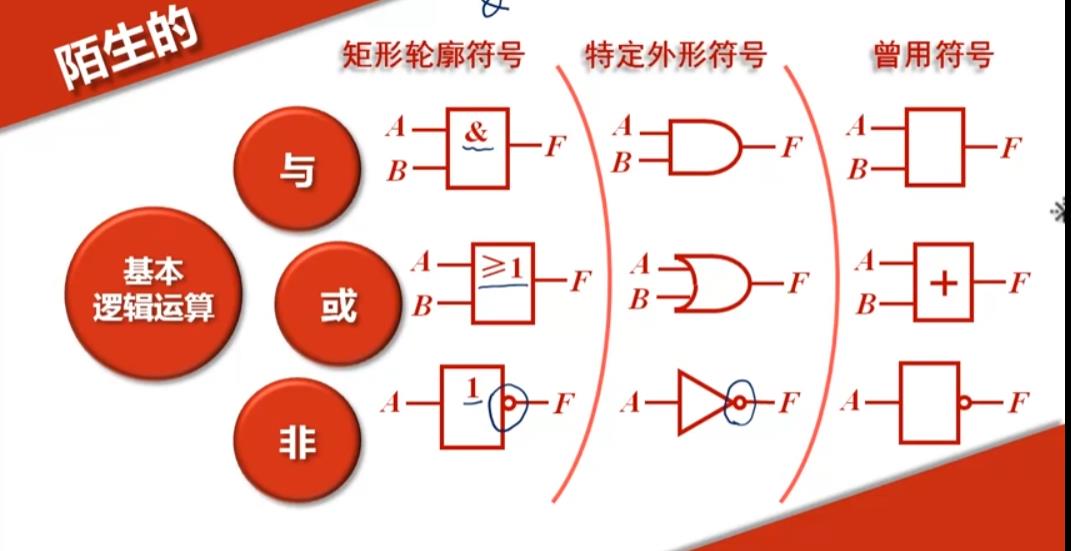
逻辑门符号是怎么来的:[中国大学MOOC 西安工业大学《数字电子技术基础》]
二.基本逻辑运算
基本逻辑运算对应基本的逻辑关系
1.与运算(逻辑乘 AND)
或叫与逻辑
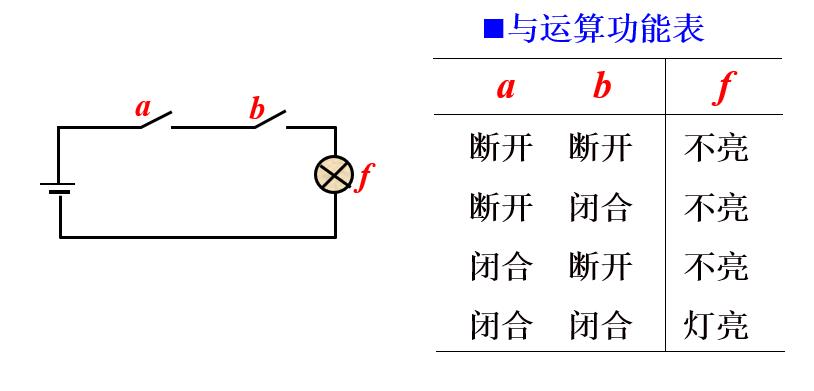
与逻辑:只有决定事件结果的全部条件同时具备时,结果才发生。
比如这个照明电路,决定灯是否能亮的条件就是开关A,B是否闭合
用0、1对条件和结果进行赋值
- a.b
- 0:断开
- 1:闭合
- f
- 0:灯灭
- 1:灯亮
于是可得真值表如下
与运算真值表
| a | b | f |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
与逻辑功能口诀
有0出0,全1出1
与运算表达式
f = a ⋅ b = a b f=a\\cdot b=ab f=a⋅b=ab
符号和代数运算中乘法一样,与运算也称为为逻辑乘法
读作a与b或a乘b
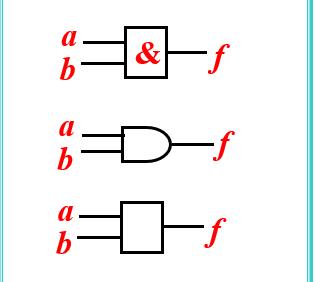
与门逻辑符号
-
表示了输入和输出是与逻辑的关系
-
另一方面也是能够实现与逻辑的电路的符号
- 实现逻辑的电路叫门
- 实现与逻辑的电路就叫与门
- 实现逻辑的电路叫门
2.或运算(逻辑加 OR)
也可叫或逻辑
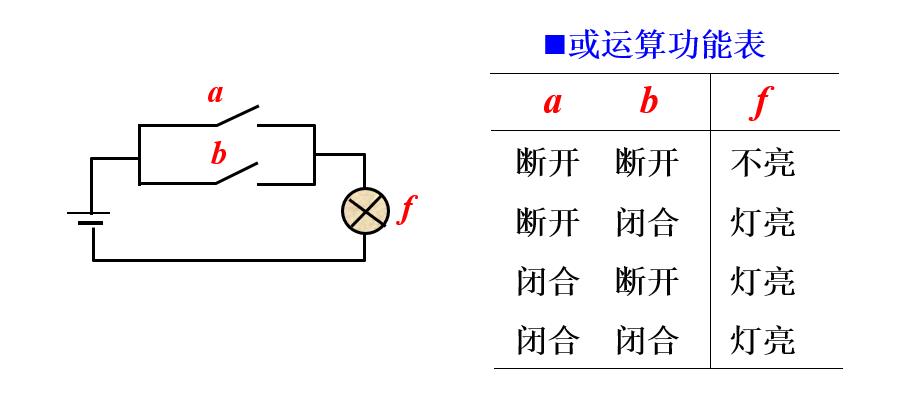
或逻辑:决定事件结果的诸条件中只要有任何一个满足,结果就会发生
仍以照明电路为例:
用0、1对条件和结果进行赋值
- a.b
- 0:断开
- 1:闭合
- f
- 0:灯灭
- 1:灯亮
或运算真值表
| a | b | f |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
或逻辑功能口诀
有1出1,全0出0
或运算表达式
f = a + b f=a+b f=a+b
符号和代数运算中加法一样,或逻辑也称为逻辑加法
读的时候读成加号也没问题 读作a或b a加b 都行
或门逻辑符号
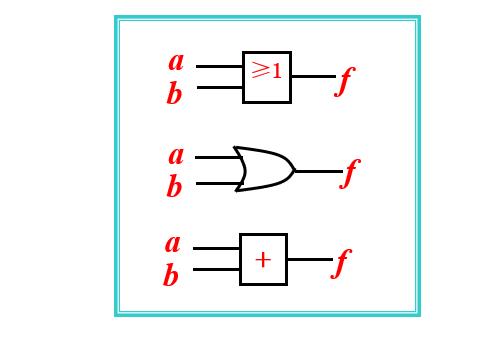
3.非运算(逻辑反 NOT)
也可叫非逻辑
- 只要条件具备了,结果就不会发生;而条件不具备时,结果一定发生
非运算真值表
| a | b |
|---|---|
| 0 | 1 |
| 1 | 0 |
非运算表达式
f = a ‾ f=\\overline{a} f=a
读作F等于A非 或 F等于A反
非门逻辑符号
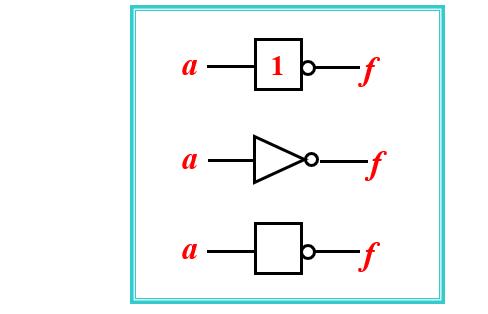
4.总结
- 真值表、运算表达式
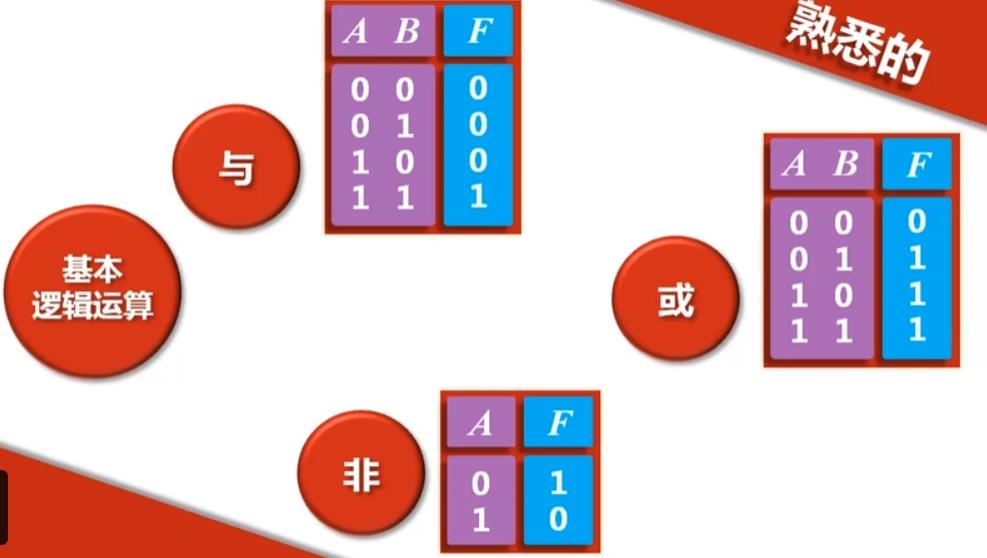
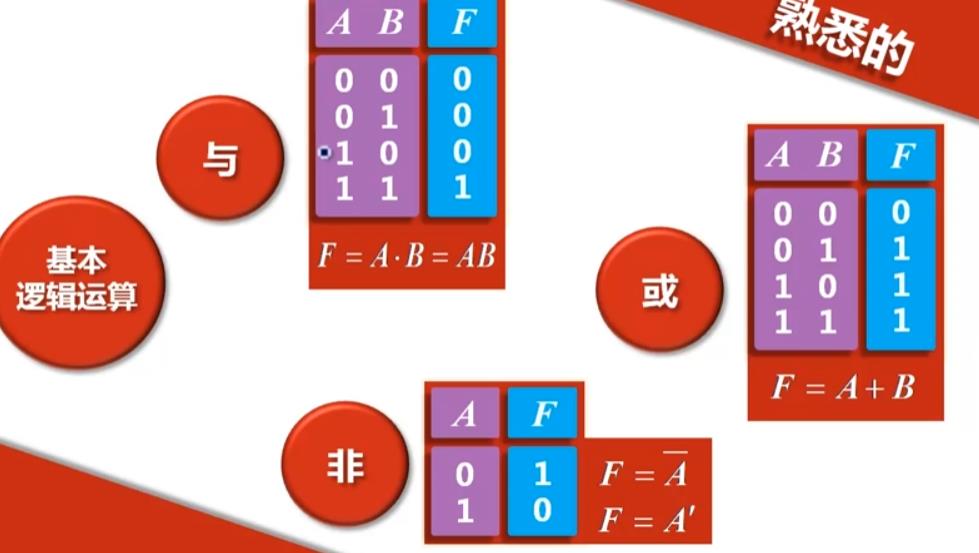
- 逻辑符号
三.复合逻辑运算
是与、或、非三种基本逻辑运算的组合
1.与非运算(NAND)
或叫与非逻辑
先与运算,再非运算
与非逻辑表达式
f = a b ‾ f=\\overline{ab} f=ab
与非逻辑真值表
| a | b | f |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
与非逻辑功能口诀
有0出1,全1出0
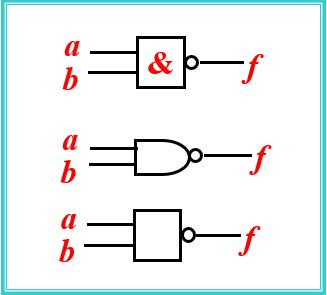
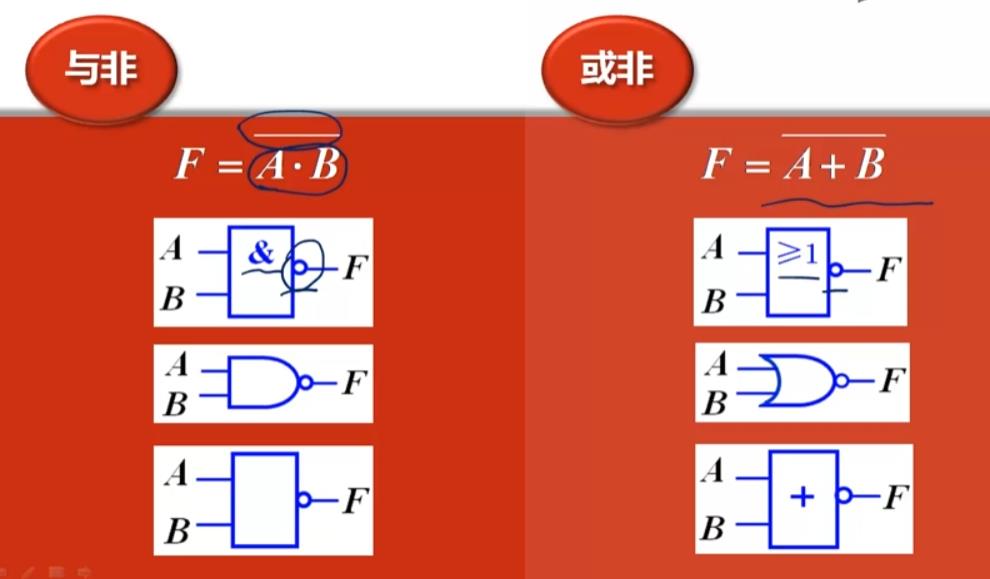
与非门逻辑符号
2.或非逻辑(NOR)
或非逻辑表达式
f = a + b ‾ f=\\overline{a+b} f=a+b
或非逻辑真值表
| a | b | f |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
或非逻辑功能口诀
有1出0,全0出1
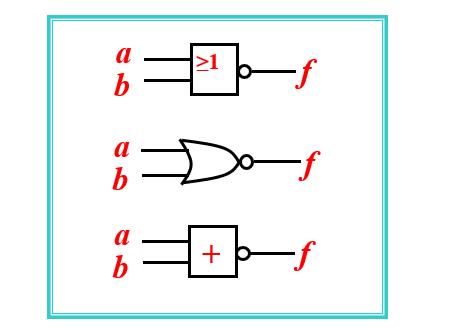
或非门逻辑符号
3.与或非运算(AND-OR-NOT)
与或非逻辑表达式
f = a b + c d ‾ f=\\overline{ab+cd} f=ab+cd
与或非真值表
| ab | cd | f |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
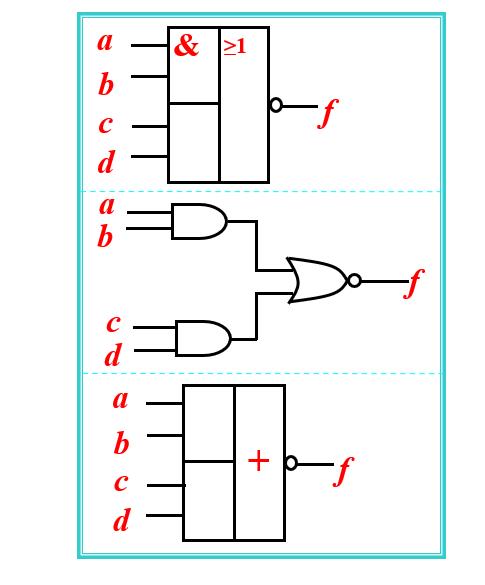
与或非门逻辑符号
4.异或运算(XOR)
异或运算输入的一定是两个变量!
异或逻辑表达式
f = a ⊕ b = a b ‾ + a ‾ b f=a\\oplus b=a\\overline{b}+\\overline{a}b f=a⊕b=ab+ab
a b反加上a反b
异或逻辑真值表
| a | b | f |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
异或逻辑功能口诀
相同为0 ,不同为1
异或门逻辑符号
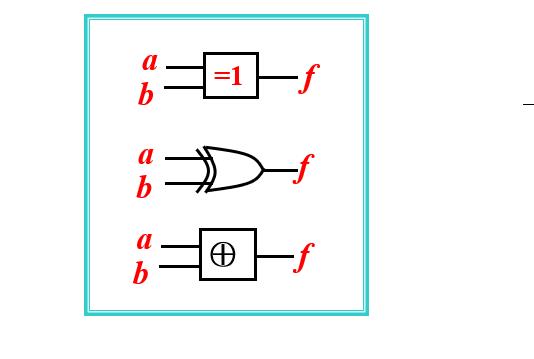
5.同或运算(XNOR)
同或逻辑表达式
f = a ⊙ b = a ‾ ⋅ b ‾ + a b f=a\\odot b=\\overline{a}\\cdot\\overline{b}+ab f=a⊙b=a⋅b+ab
a反b反 加上 ab
同或逻辑真值表
| a | b | f |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
同或逻辑功能口诀
相同为1 ,不同为0
同或门逻辑符号
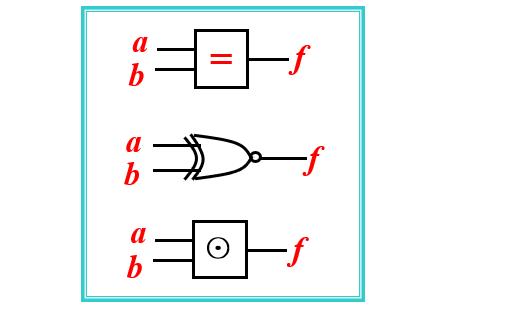
异或和同或互为反运算
A ⊕ B = A ⊙ B ‾ A\\oplus B=\\overline{A\\odot B} A⊕B=A⊙B
A B ˙ = A ⊕ B ‾ A\\dot B=\\overline{A\\oplus B} AB˙=A⊕B
6.总结
与非、或非、与或非
- 有很多现实逻辑命题很复杂,不能简单套用常见的逻辑,要自己去分析,画出真值表

-
利用真值表的整体分析法可以避免复杂的代入运算
- 根据逻辑关系进行整体逆推

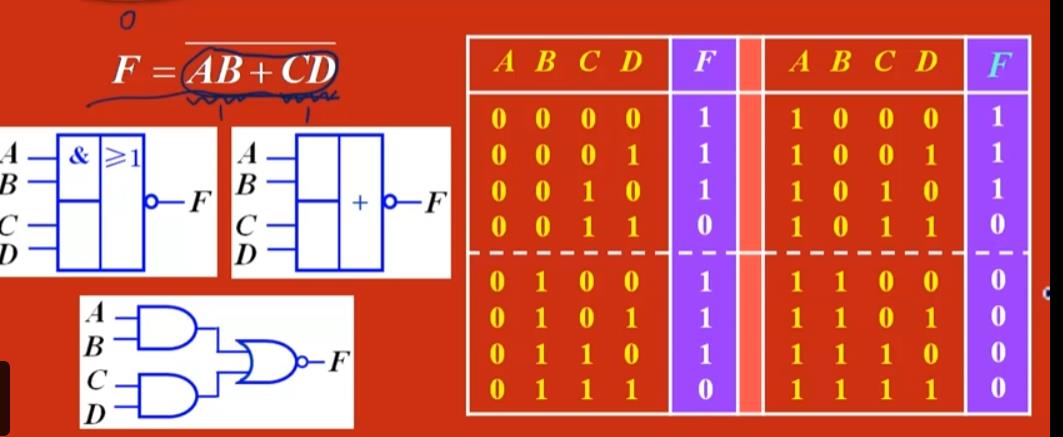
先从F何时为0开始分析
那就是AB+CD为1,也就是AB为1或CD为1 也就是A、B均为1 或者 C、D均为1
这些情况找出来了, 剩下的就是F为1的情况了
异或、同或
表达式

自有表达式 A ⊕ B A\\oplus B A⊕B就读作 A异或B A ⊙ B A\\odot B A⊙B就读作A同或B
组合表达式也要牢记
名称

注意同或只是有时能叫异或非
2输入异或、同或的功能

逻辑门符号
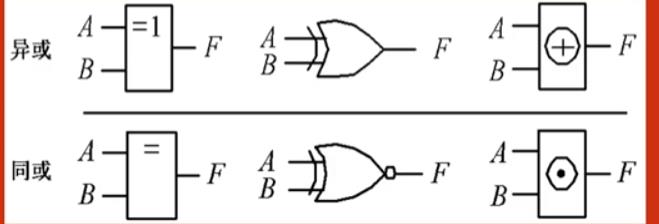
四个结论
-
2输入异或、同或的功能

-
2输入异或、同或的关系
- 互为反函数,即非关系
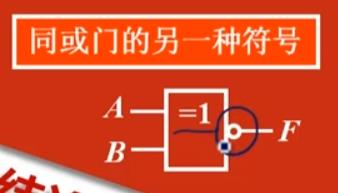
- 同或的另一种逻辑门可以看成异或非
-
n输入异或的功能
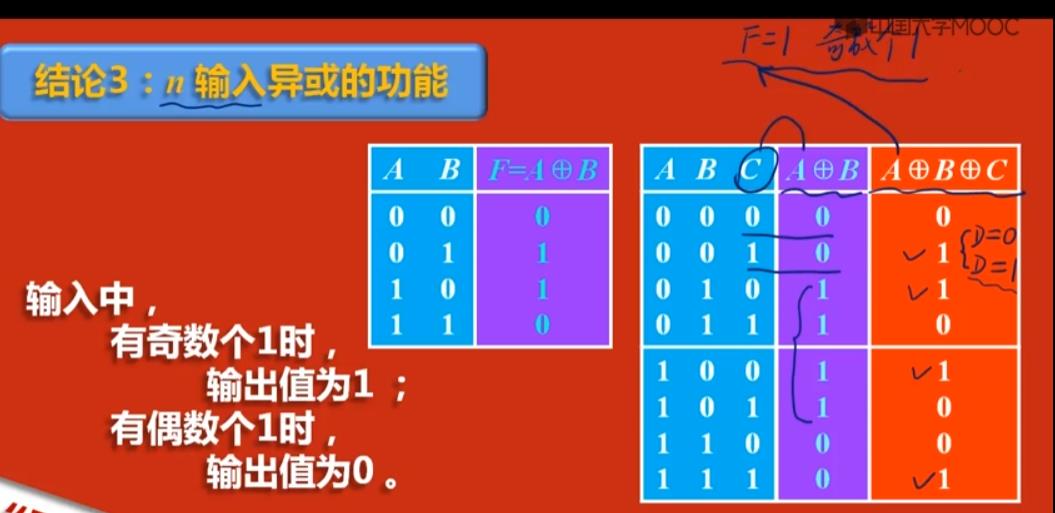
- 检奇/检偶功能
-
n输入异或、同或的关系
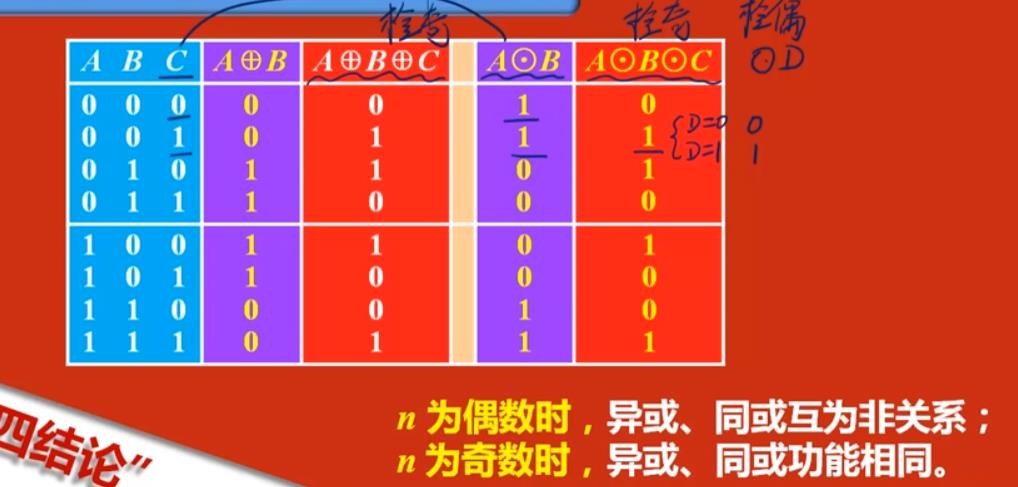
- n为奇数时 异或 同或 都在检验1的个数是否为奇数
- n为偶数时 异或仍然在“检奇” 同或在“检偶”
核心
- n为奇数,同或在“检奇”
- n为偶数,同或在“检偶”
§2.2逻辑代数的基本定律和运算规则
一.逻辑代数的基本定律
重点
①几个简单定律
| 定律 | 公式1 | 公式2 |
|---|---|---|
| 0-1律 |
1
⋅
A
=
A
1\\cdot A=A
1⋅A=A 0 ⋅ A = 0 0\\cdot A=0 0⋅A=0 |
1
+
A
=
1
1+A=1
1+A=1 0 + A = A 0+A=A 0+A=A |
| 重叠律 | A ⋅ A = A A\\cdot A=A A⋅A=A | A + A = A A+A=A A+A=A |
| 互补律 | A ⋅ A ‾ = 0 A\\cdot \\overline {A}=0 A⋅A=0 | A + A ‾ = 1 A+\\overline{A}=1 A+A=1 |
公式1,公式2 互为对偶关系
| 定律 | ||
|---|---|---|
| 还原率 | A = = A \\overset{\\text{=}}{A}=A A==A |
一个变量经过两次求反运算后还原为其本身,故称还原律
②交换律、结合律、分配律
| 定律 | 公式1 | 公式2 |
|---|---|---|
| 交换律 | A ⋅ B = B ⋅ A A\\cdot B=B\\cdot A A⋅B=B⋅A | A + B = B + A A+ B=B+ A A+B=B+A |
| 结合律 | A ⋅ ( B ⋅ C ) = ( A ⋅ B ) ⋅ C A\\cdot (B \\cdot C)=(A\\cdot B)\\cdot C A⋅(B⋅C)=(A⋅B)⋅C | A + ( B + C ) = ( A + B ) + C A+ (B +C)=(A+ B)+ C A+(B+C)=(A+ |