数字电路再学习之逻辑代数基础

Posted 2021-09-25 学工科的皮皮志^_^

文章目录

• 前言
• 一、概述
• 二、逻辑代数中的三种基本运算
• • 1.与门
  • 2.或门
  • 3.非门
  • 4.真值表
  • 5.几种常见的符合逻辑运算
  • 6、异或
  • 7.同或
• 三、逻辑代数中的基本公式和常用公式
• 四、逻辑代数的基本定理
• • 4.1代入定理
  • 4.2 反演定理
  • 4.3对偶定理
• 总结

---

前言

上一讲我们学习了数字电路再学习之（一）数制和码制
今天我们学习逻辑代数基础

一、概述

只有2种对立的逻辑状态时称二值逻辑。

●用字母表示逻辑变量，每个逻辑变量的取值只有0和1两种可能，0和1不表示大小，只表示逻辑状态。

●当两个二进制数码表示不同的逻辑状态时，可以按照指定的某种因果关系进行推理运算，即逻辑运算。

二、逻辑代数中的三种基本运算

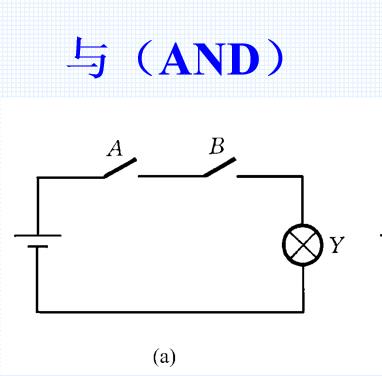
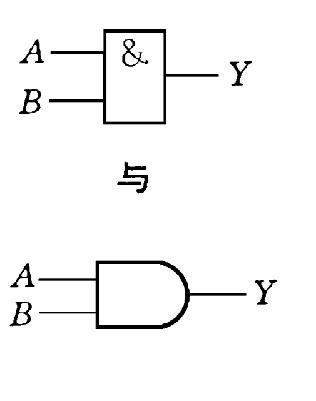
1.与门

2.或门

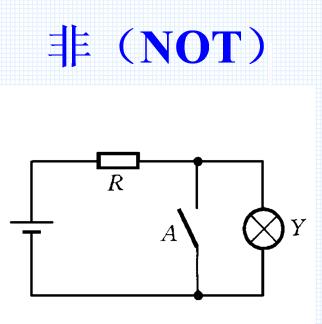
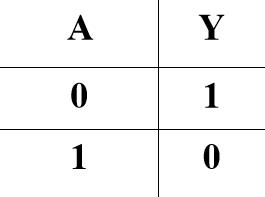
3.非门

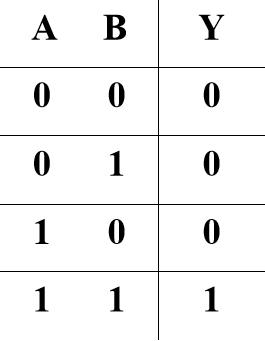
4.真值表

与：
条件同时具备，结果发生
Y=A AND B = A&B=A·B=AB


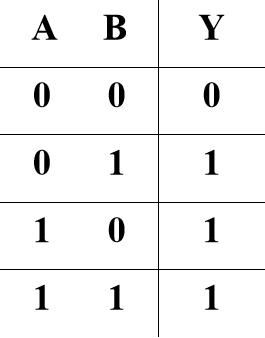
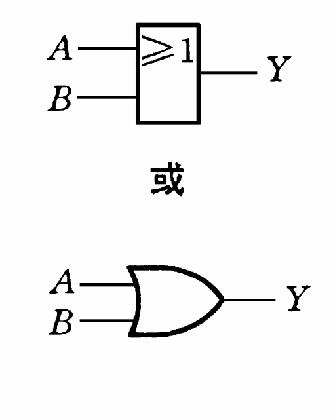
或
条件之一具备，结果发生
Y= A OR B = A+B


非门

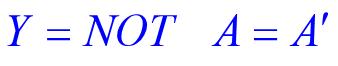
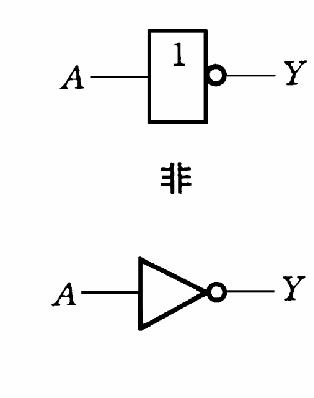
5.几种常见的符合逻辑运算

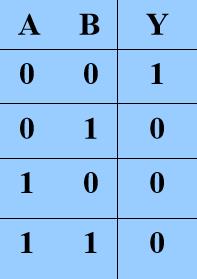
== 与非==

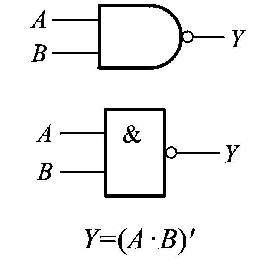
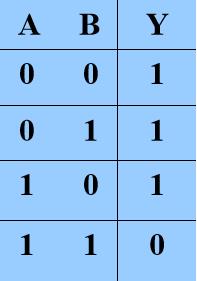
或非

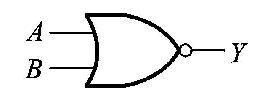
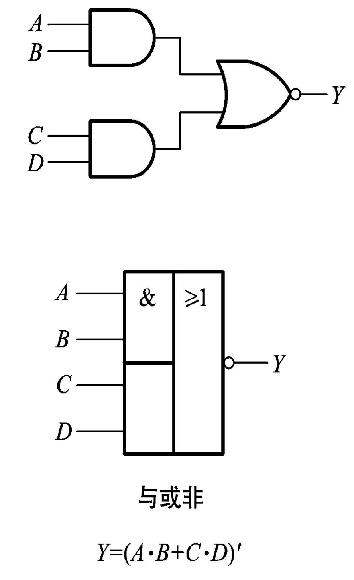
与或非

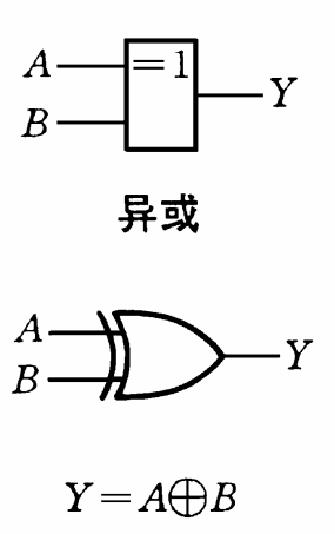
6、异或

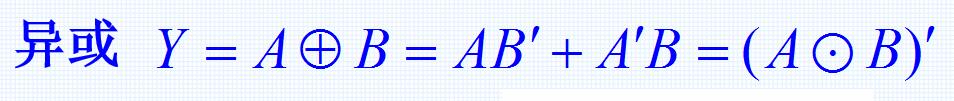
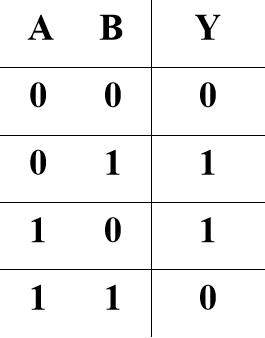
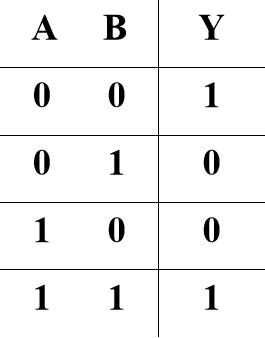
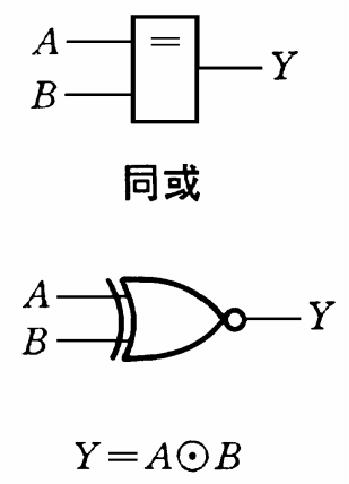
7.同或

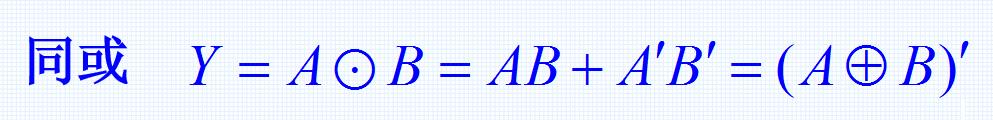
三、逻辑代数中的基本公式和常用公式

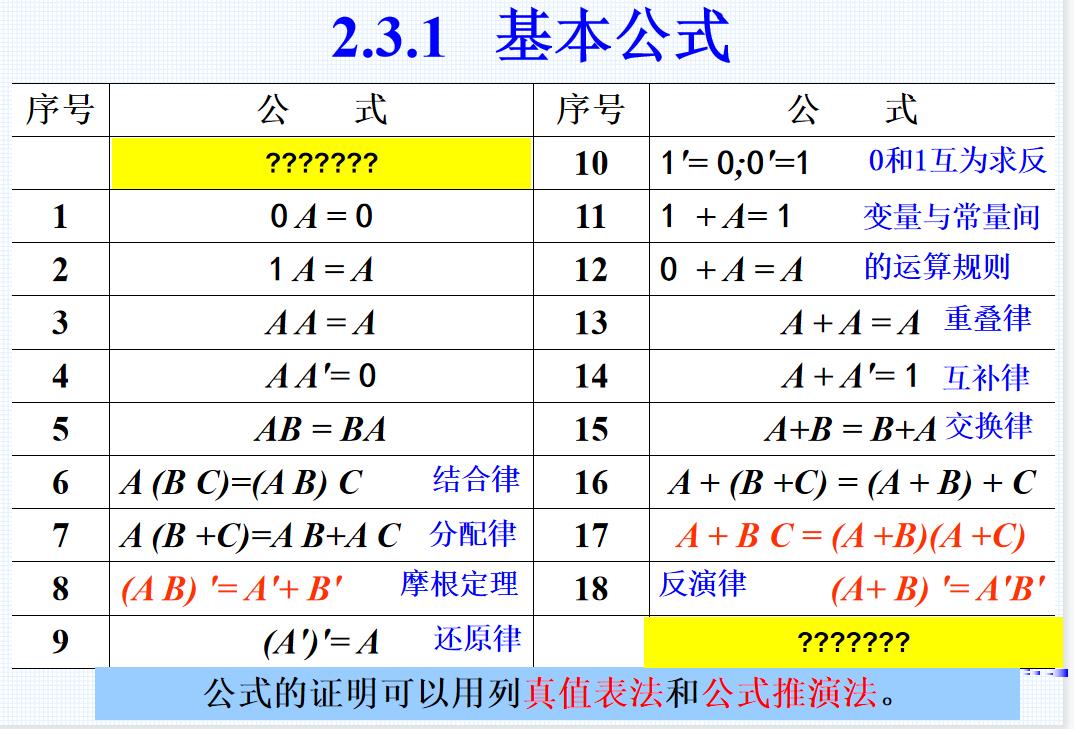
公式（17）A + B C = (A +B)(A +C) 的证明

常有的若干公式

四、逻辑代数的基本定理

4.1代入定理

定理内容： 在任何一个包含变量A的逻辑等式
中，若以另外一个逻辑式代入式中所有A的位
置，则等式仍然成立。
注意事项：需遵守与普通代数一样的运算优先
顺序，即先括号内，再乘法，最后加法。

代入定理应用举例1

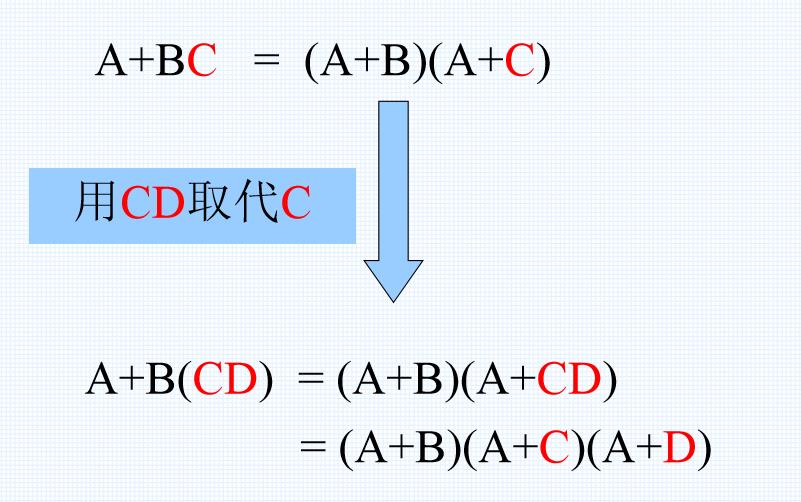
代入定理应用举例2——

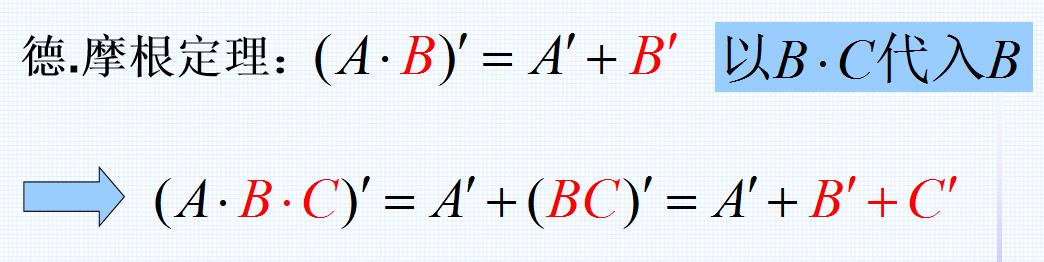
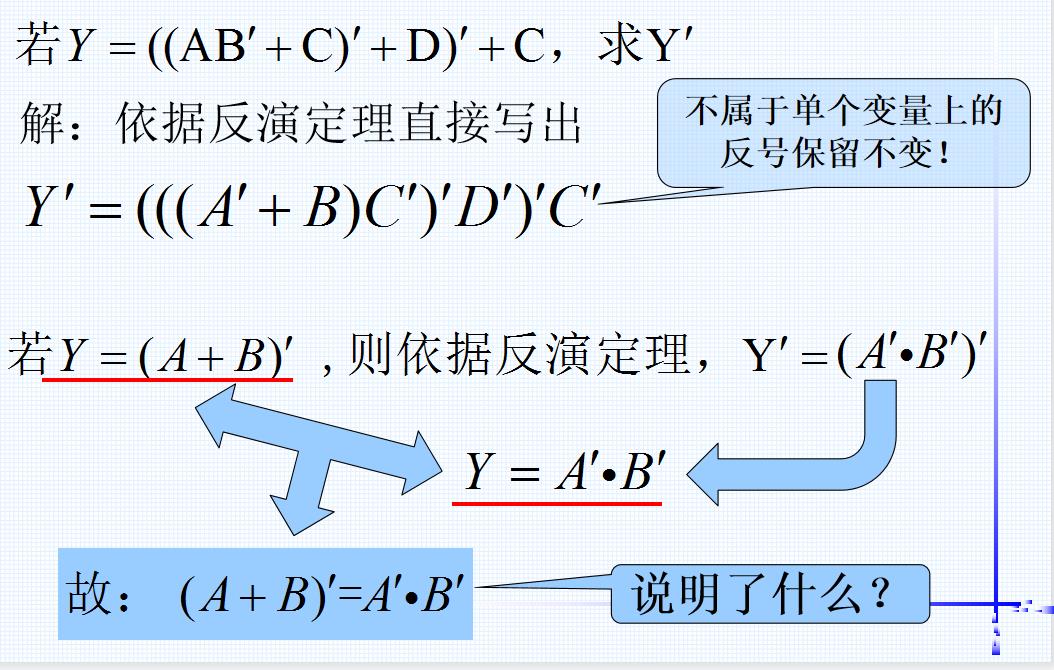
4.2 反演定理

定理内容：对任一逻辑式

注意事项：变换顺序是先括号，然后乘， 最后加，不属于单个变量上的反号保留不变。
反演定理应用举例1——

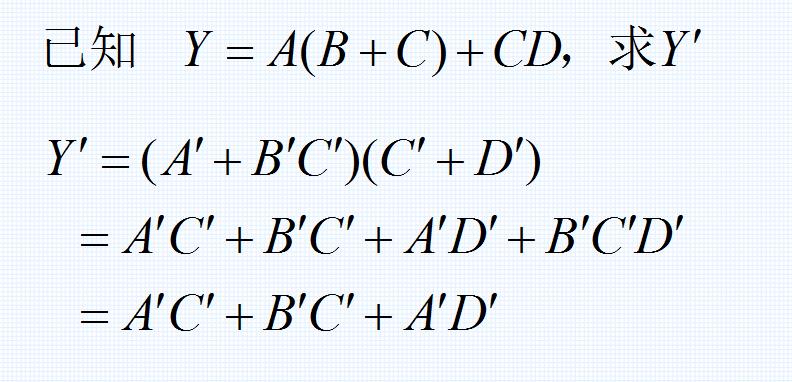
反演定理应用举例2——

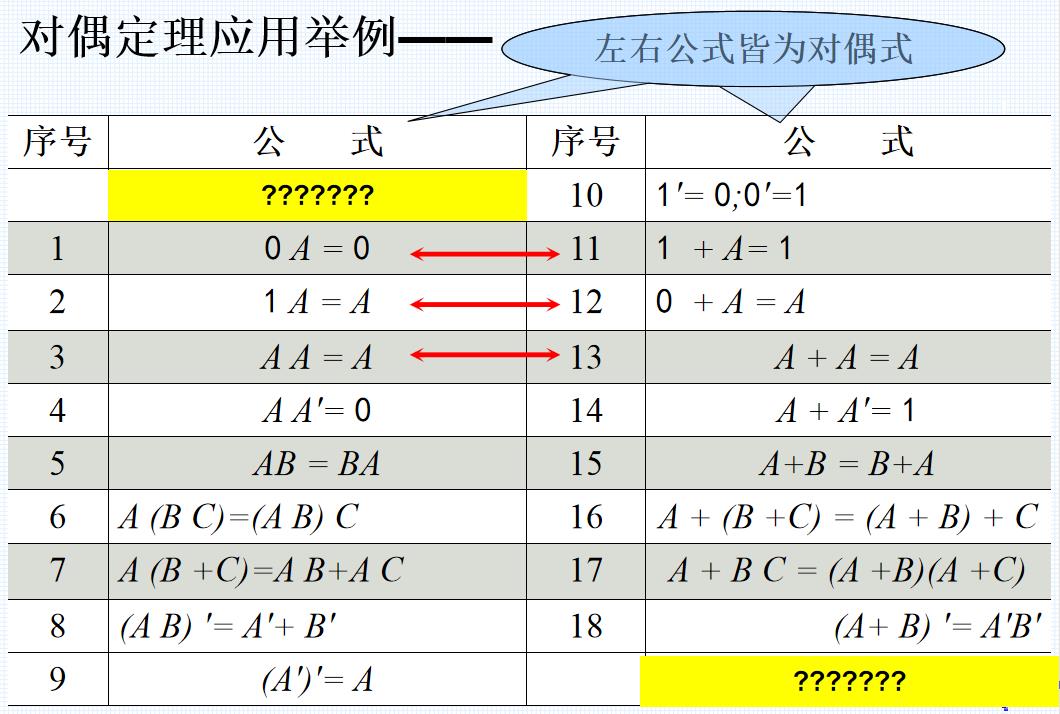
4.3对偶定理

定理内容：若两逻辑式相等，则它们的对偶式也
相等。

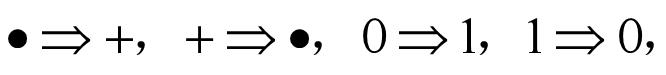
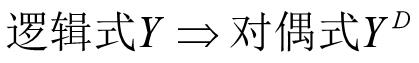
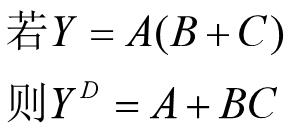
总结

以上就是今天要讲的内容