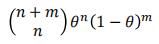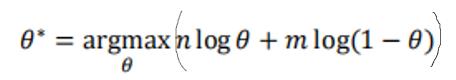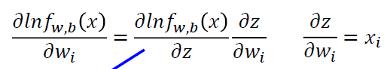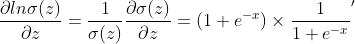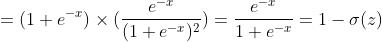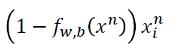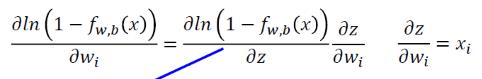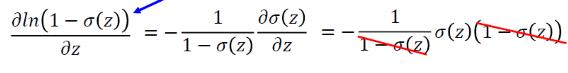机器学习笔记:logistic regression
Posted UQI-LIUWJ
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习笔记:logistic regression相关的知识,希望对你有一定的参考价值。
1 逻辑回归介绍
logistic regressioin是一种二分类算法,通过sigmoid激活函数将线性组合压缩到0和1之间,来代表属于某一个分类的属性
虽然其中带有"回归"两个字,但逻辑回归其实是一个分类模型
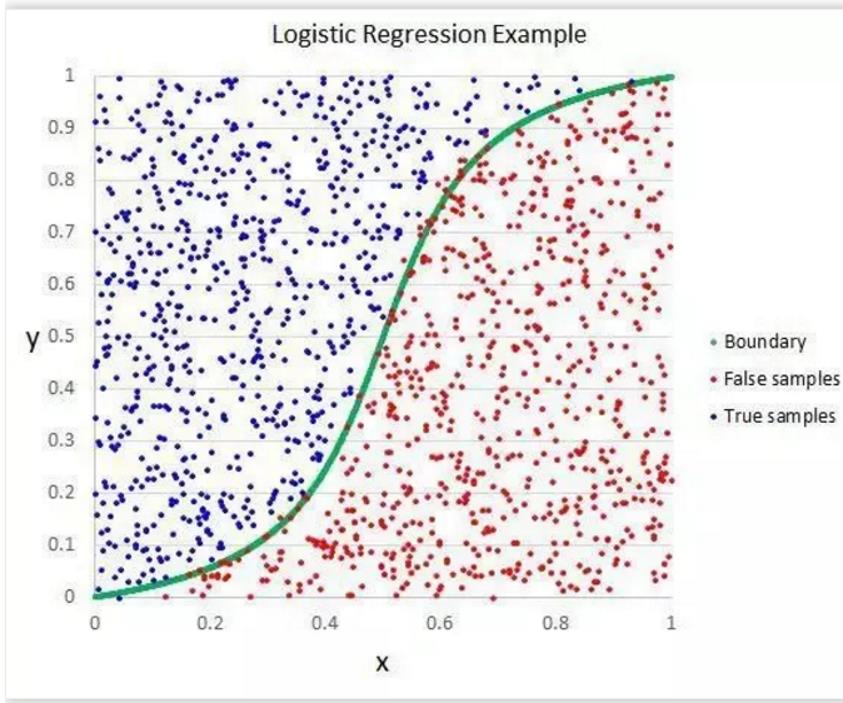
好处在于输出值自然地落在0到1之间,并且有概率意义。模型清晰,有对应的概率学理论基础。
但同时由于其本质上是一个线性的分类器,所以不能应对较为复杂的数据情况。很多时候我们也会拿逻辑回归模型去做一些任务尝试的baseline
2 三步法解释逻辑斯蒂回归
还是使用李宏毅教授所说的深度学习三步法来理解模型:
2.1 Step 1 function set
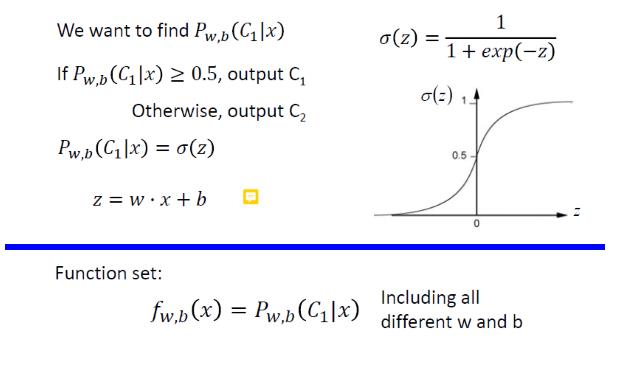
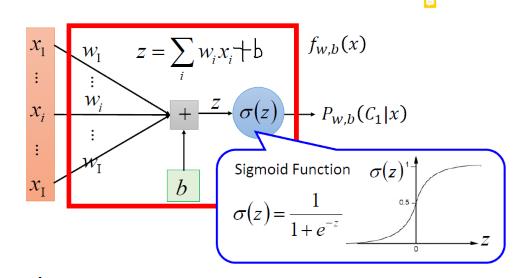
2.1.1 sigmoid
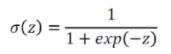
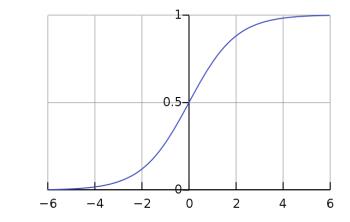
将所有结果压缩到[0~1]上——可以用来进行二元分类,σ(x)表示了一个类的概率
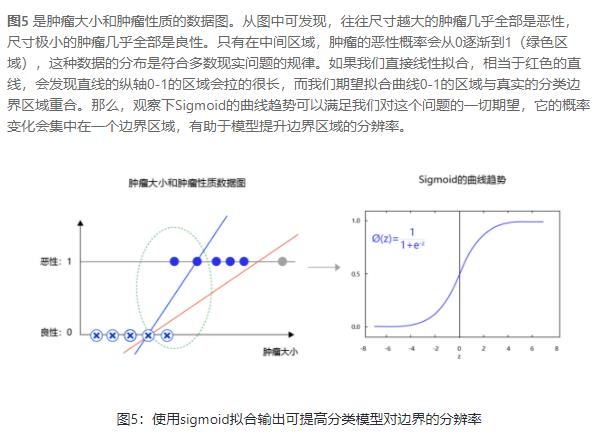
2.1.2 sigmoid的好处
2.2 Step2 goodness of a function
C1的概率是f,那么C2的概率就是1-f

我们引入交叉熵
交叉熵判断两个分布的相似程度,如果两个分布一模一样,那么交叉熵最小(除非两个分布都是one-hot,否则不可能交叉熵是0)
交叉熵能够衡量同一个随机变量中的两个不同概率分布的差异程度,在机器学习中就表示为真实概率分布与预测概率分布之间的差异。交叉熵的值越小,模型预测效果就越好。
交叉熵在分类问题中常常与softmax是标配,softmax将输出的结果进行处理,使其多个分类的预测值和为1,再通过交叉熵来计算损失。
2.2.1 从最大似然估计的角度理解交叉熵
对于一个随机变量,假设类别1的概率是θ,类别0的概率是1-θ
那么,出现n次1和m次0的概率是:
取log+极大似然估计,有:
将上式对θ求导,有
,结果也是符合直观的
我们引入逻辑斯蒂回归的损失函数:交叉熵
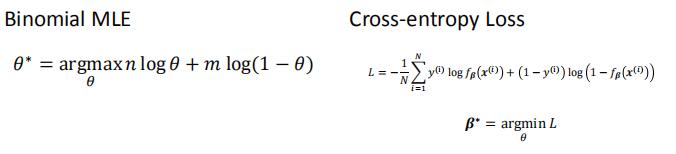
2.3 Step 3 find best function
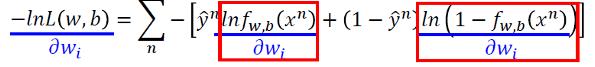
我们首先看
我们令
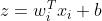
那么我们有:
与此同时,我们有:
(σ是sigmoid函数)
所以有
(
)
所以
=
然后我们看
同样令
所以
=
综合起来,有:

3 逻辑斯蒂回归和线性回归

4 能否用均方误差代替交叉熵
我们考虑一下logistic regression+MSE
也就是说,无论我们预测的是0还是1,我们对应的梯度都是0
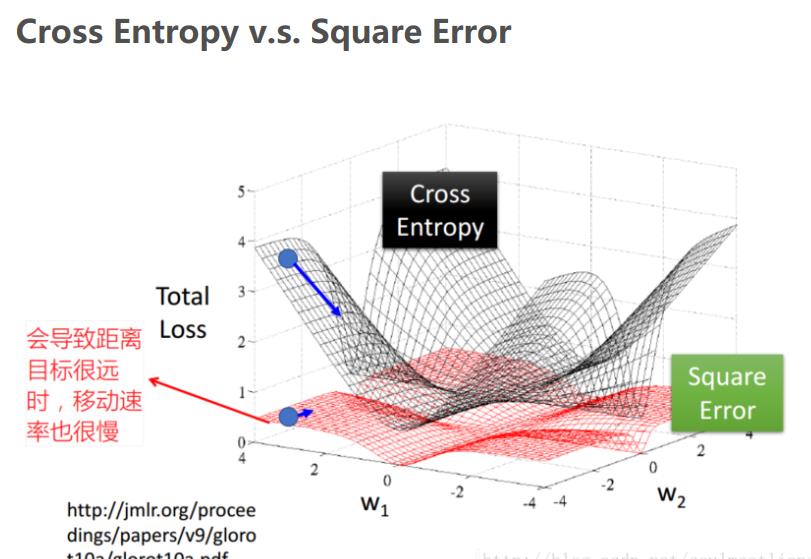
也就是,在远离target的地方,我们也更新的很慢(但因为我们不知道到底现在是靠近target,还是远离target,所以我们也不能通过调整学习率)
4 从极大似然估计的角度看逻辑回归


以上是关于机器学习笔记:logistic regression的主要内容,如果未能解决你的问题,请参考以下文章