线性代数本质1:向量究竟是什么
Posted 快乐江湖
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了线性代数本质1:向量究竟是什么相关的知识,希望对你有一定的参考价值。
一:不同的人如何看待向量
向量的概念我们再熟悉不过了,他们在不同人眼中是不一样的

学物理的人认为,向量是空间里面的箭头,决定一个向量的是它的方向和长度,如果两个向量这两个特征相同,那么你可以在空间中任意移动
-
二维向量

-
三维向量

学计算机的人认为,向量是有序的数字列表,试图通过一组数字(顺序不可颠倒)去描述(专业叫建模)描述某个对象

对于学数学的人,他们觉得向量可以是任何东西,只要保证两个向量相加以及数字与向量相乘是有意义的即可

可以看出为什么从数学的角度看,向量是相当抽象的,这也是为什么我们无法学好线性代数的本质,而且向量相加和数乘也贯穿了线性代数这门学科的始终、
二:坐标系中的向量表示
在线性代数中,我们的向量是一个以坐标原点为起点的箭头(下面的是二维直角坐标系,三维,更高维也是这样)
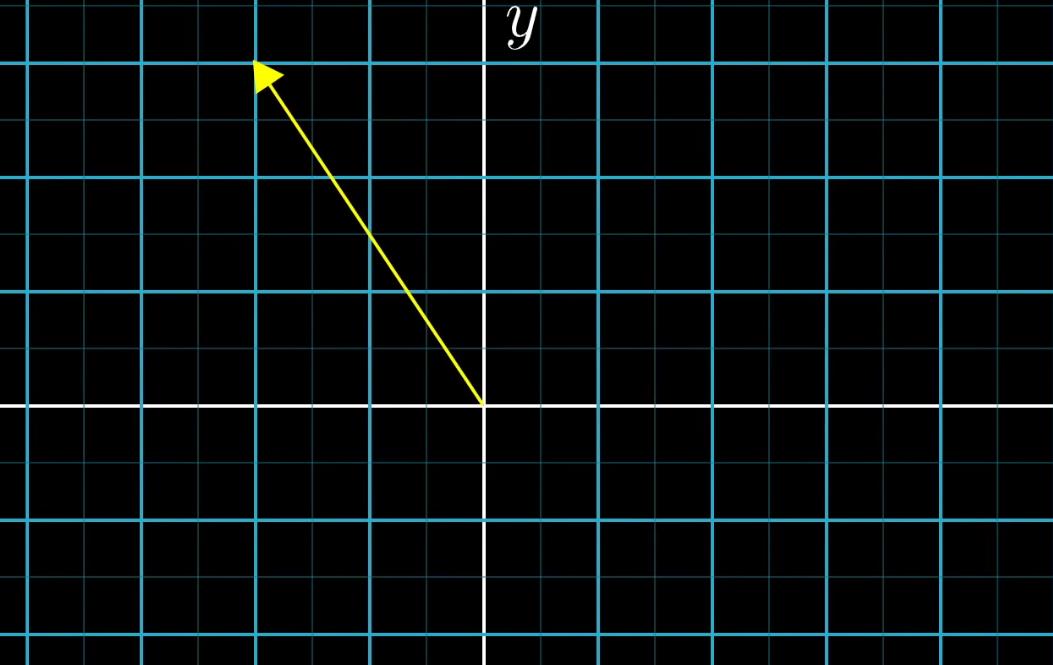
我们经常会见到线性代数中用 ( − 2 3 ) \\begin{pmatrix} -2\\\\ 3\\end{pmatrix} (−23)这样的形式表示向量,这一对数表示了如何从原点(向量起点)到达尖端(向量终点)
- -2表示从原点开始沿着平行于X轴的负方向移动两个单位
- 3表示从上一位置开始沿着平行于Y轴的正方向移动两个单位

每一对数给出了唯一的一个向量,而每一个向量又恰好对应唯一一对数
当然我们处于三维世界,也是如此,会多一个z轴,这样的话每一向量就会与一个三元数组对应,比如 ( 2 1 3 ) \\begin{pmatrix} 2\\\\ 1\\\\ 3\\end{pmatrix} ⎝⎛213⎠⎞
- 2表示从原点开始沿着平行于X轴的正方向移动两个单位
- 1表示从上一位置开始沿着平行于Y轴的正方向移动一个单位
- 3表示从上一位置开始沿着平行于Z轴的正方向移动三个单位

三:坐标系中向量加法和数乘
(1)相加
我们都很熟悉向量加法的规则:
(
1
2
)
\\begin{pmatrix} 1\\\\ 2\\end{pmatrix}
(12)+
(
3
−
1
)
\\begin{pmatrix} 3\\\\ -1\\end{pmatrix}
(3−1)=
(
4
1
)
\\begin{pmatrix} 4\\\\ 1\\end{pmatrix}
(41)
但为什么要这样运算,很多人却解释不清楚,不过通过几何角度会非常容易理解。
首先
(
1
2
)
\\begin{pmatrix} 1\\\\ 2\\end{pmatrix}
(12)和
(
3
−
1
)
\\begin{pmatrix} 3\\\\ -1\\end{pmatrix}
(3−1)这两个向量在坐标系中表示如下

向量加法相信大家高中就学习过了:移动第二个向量,使其起点移动到第一个向量的末尾,然后连线即可
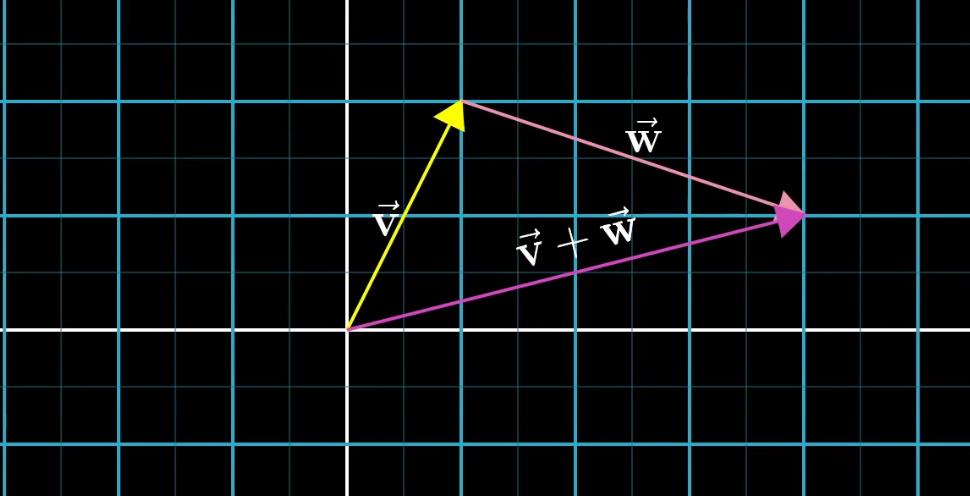
向量加法为什么一定是这样呢?其实向量从某种方面来讲,揭示的是一种运动趋势,运动无非就是方向和距离嘛,所以大家可以看到最终向量的和就是最终的运动趋势。
这一点其实在我们初中学习数轴时就深有体会了,我们知道2+5=7,你可以理解为先移动2步,再移动5步

我们把这种观点运用到刚才的向量加法,两个向量相加最终得到了一个新的向量,它一共包括四步:先向右移动1步,再向上移动2步,再向右移动3步,再向下移动1步
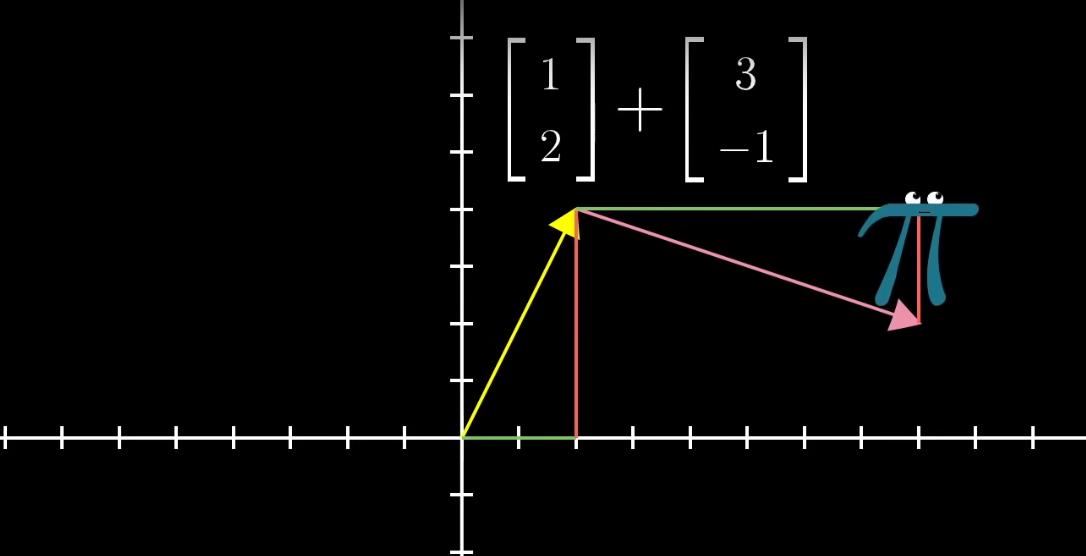
所以这就是向量加法的本质

(2)数乘
2· ( 1 2 ) \\begin{pmatrix} 1\\\\ 2\\end{pmatrix} (12)= ( 2 4 ) \\begin{pmatrix} 2\\\\ 4\\end{pmatrix} (24)就是向量的数乘运算
比如
2
v
‾
2\\overline v
2v就是表示把
v
‾
\\overline v
v正向延长为原来的2倍

1
3
v
‾
\\frac{1}{3} \\overline v
31v就是表示把
v
‾
\\overline v
v正向缩短为原来的
1
3
\\frac{1}{3}
31

而
−
1.8
v
‾
-1.8\\overline v
−1.8v就是表示把
v
‾
\\overline v
v反向延长为原来的1.8倍

对于一个向量,对其进行延长2倍等于把它的每个分量都乘以2,也即
2·
(
1
3
)
\\begin{pmatrix} 1\\\\ 3\\end{pmatrix}
(13)=
(
1
×
2
3
×
2
)
\\begin{pmatrix} 1×2\\\\ 3×2\\end{pmatrix}
(1×23×2) =
(
2
6
)
\\begin{pmatrix} 2\\\\ 6\\end{pmatrix}
(26)
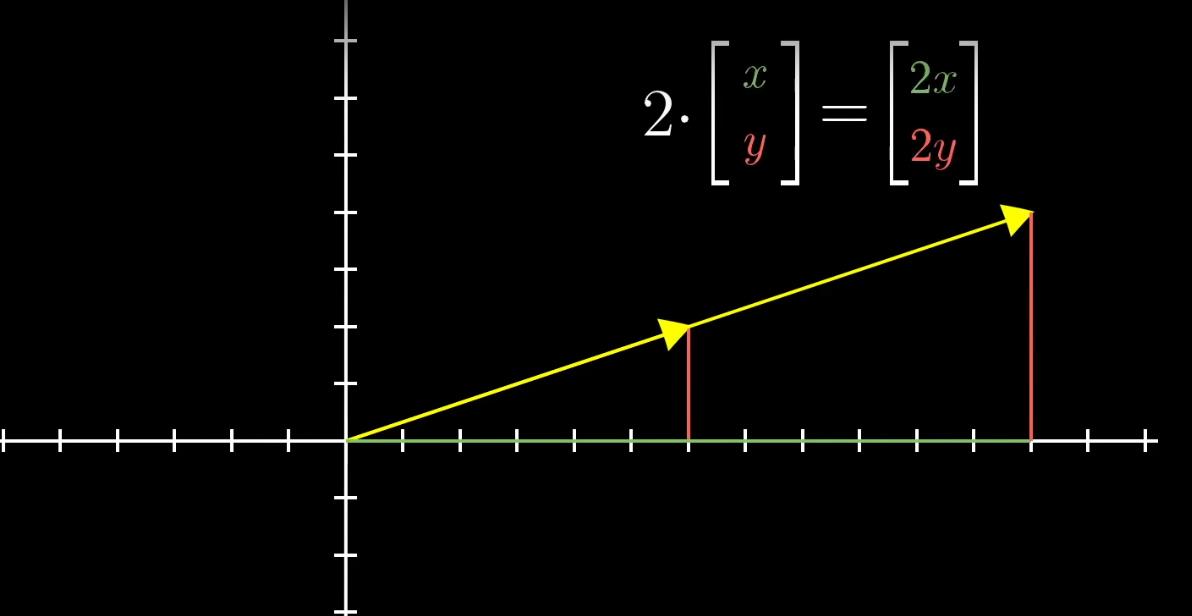
到这里向量,就基本介绍完毕了,大家一定要深刻理解,线性代数本质就是向量,而向量既可以用箭头表示也可以用有序数组表示,这些花里胡哨的表示方式并不是为了好看,实际是为了方便我们用数字操控空间,用空间表示数字等等


以上是关于线性代数本质1:向量究竟是什么的主要内容,如果未能解决你的问题,请参考以下文章