归并排序及其应用场景
Posted 森明帮大于黑虎帮
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了归并排序及其应用场景相关的知识,希望对你有一定的参考价值。
一、归并排序的概念

二、归并排序递归与非递归实现
归并排序递归实现,分治为每个区间元素都有序,那么就得把区间 分治成为1才能保证区间中每个元素都有序,在归并:
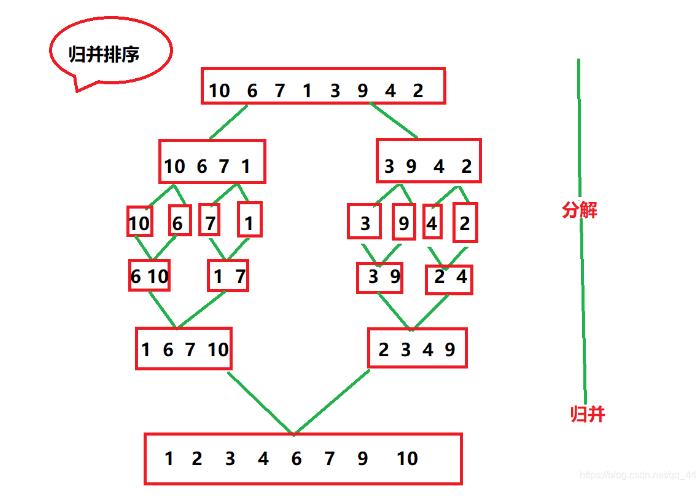
//归并排序
void _MergeSort(int*arr, int left, int right, int* tmp)
{
if (left >= right)
{
return;
}
int mid = left + (right - left) / 2;
_MergeSort(arr, left, mid, tmp);
_MergeSort(arr, mid + 1, right, tmp);
int begin1 = left;
int end1 = mid;
int begin2 = mid + 1;
int end2 = right;
int i = left;
while (begin1 <= end1&&begin2 <= end2)
{
if (arr[begin1] < arr[begin2])
{
tmp[i++] = arr[begin1++];
}
else if (arr[begin1]>arr[begin2])
{
tmp[i++] = arr[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = arr[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = arr[begin2++];
}
for (int j = left; j <= right; j++)
{
arr[j] = tmp[j];
}
}
void MergeSort(int* arr, int sz)
{
int* tmp = new int[sz];
_MergeSort(arr, 0, sz - 1, tmp);
delete[] tmp;
}
归并排序非递归实现 ,借助gap值来归并:
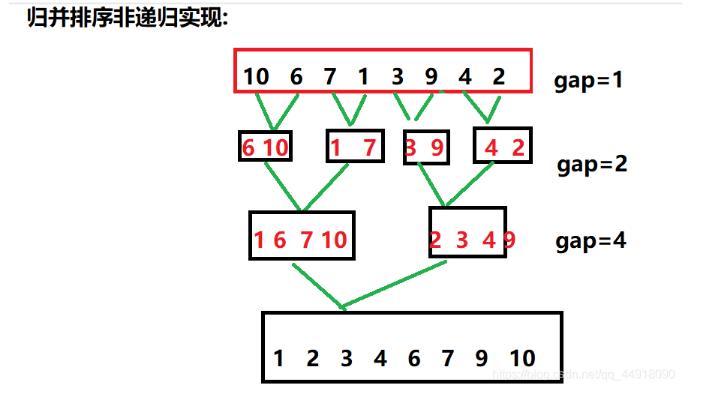
注意归并时候发生的三种情况:

void _MergeSortNonR(int* arr, int begin1, int end1, int begin2, int end2, int* tmp)
{
int i = begin1;
int j = begin1;
while (begin1 <= end1&&begin2 <= end2)
{
if (arr[begin1] < arr[begin2])
{
tmp[i++] = arr[begin1++];
}
else
{
tmp[i++] = arr[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = arr[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = arr[begin2++];
}
for (; j <= end2; j++)//begin1加加j不受到影响
{
arr[j] = tmp[j];
}
}
void MergeSortNonR(int* arr, int sz)
{
int* tmp = new int[sz];
int gap = 1;
while (gap < sz)
{
for (int i = 0; i < sz; i += 2 * gap)
{
int begin1 = i;
int end1 = i + gap - 1;
int begin2 = i + gap;
int end2 = i + 2 * gap - 1;
//如果第二个小区间不存在了
if (begin2 >= sz)
{
break;
}
//如果第二个小区间存在,但是第二个小区间不够gap个,结束位置就越界了,需要修正一下
if (end2 >= sz)
{
end2 = sz - 1;
}
_MergeSortNonR(arr, begin1, end1, begin2, end2, tmp);
}
}
}
三、归并排序应用场景


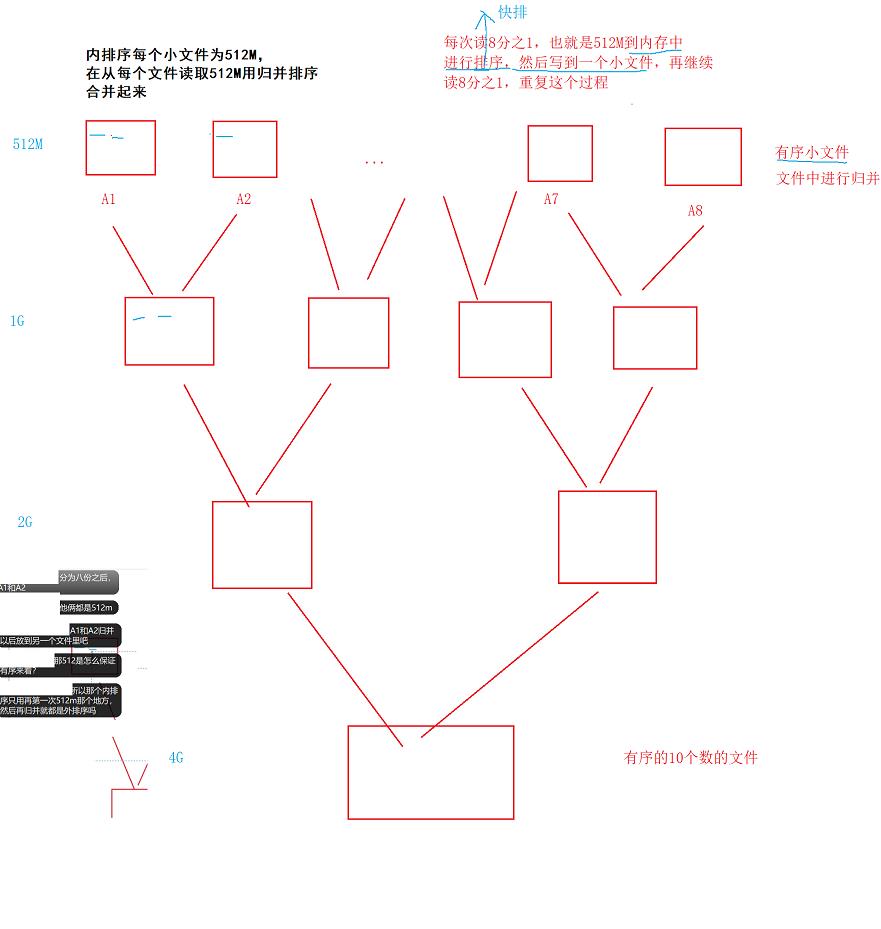
四、归并排序总结

以上是关于归并排序及其应用场景的主要内容,如果未能解决你的问题,请参考以下文章