矩阵快速幂EOJ EOJ Monthly 2021.9 Sponsored by TuSimple A. Amazing Discovery

Posted 2021-09-28 biu~跃哥冲冲冲

Problem A: Amazing Discovery

评测传送门
蒟蒻赛时就开了这么一个题，推了好久也还是推不出来😣
看了人家官方题解后，顺利AC。但是，这个推导过程有点搞怪啊，不是看了题解，我还真推不出来这个递推关系。

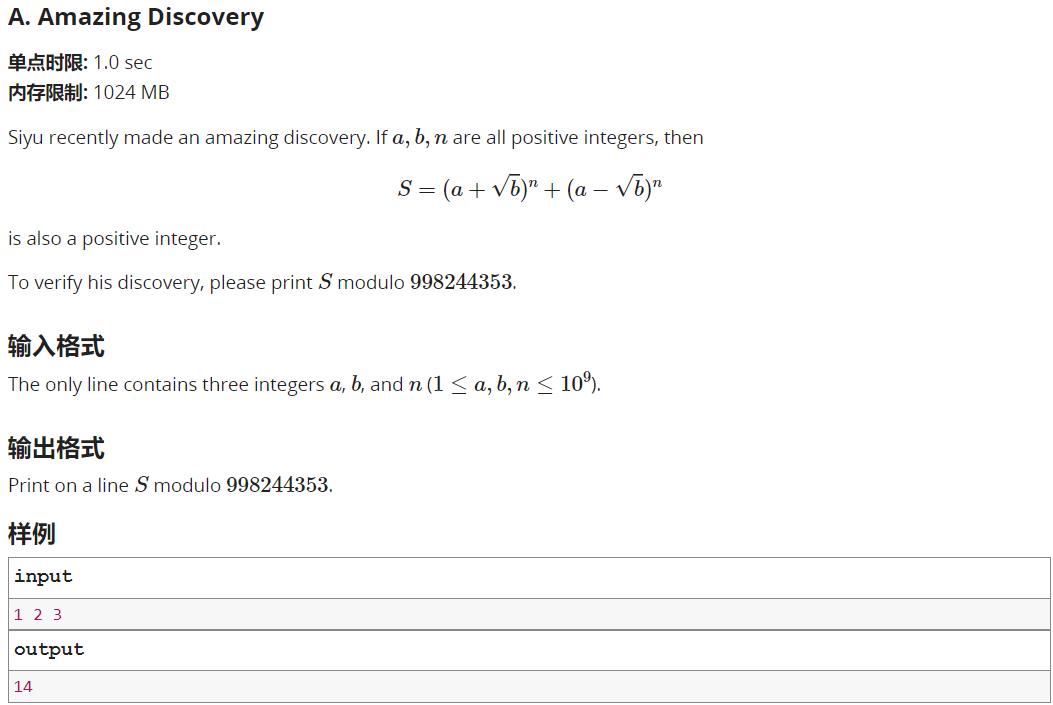
官方题解：
题解传送门

下面我提供一些推导过程中的式子，可自行代入验证一波。
这里提供一个可以进行数学计算的超强👉代数计算工具网站
$S_1=2a$
$S_2=2a^2+2b$
$S_3=2a^3+6ab$
$S_4=2a^4+2b^2+12a^{2}b$
$S_5=2a^5+10a{b}^2+20a^{3}b$
$S_5=2a\ast S_4-(a^2-b)S_3$
矩阵快速幂中A矩阵的构造：
$[S_n,S_{n+1}]$ × $A$ = $[S_{n+1},S_{n+2}]$

$$A=\begin{array}{c}\left[\begin{array}{cc}0& b-a^2\\ 1& 2a\end{array}\right]\end{array}$$
初始矩阵为：$F0=[2,2a]$
之后直接矩阵快速幂计算即可。
AcCoding:

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
const int mod = 998244353;
const int N = 2;
/*
2a * S[n-1] - S[n] = (a - b * b) * S[n - 2]
f0[2] = {S[n],S[n+1]}
A = {
	{0,2a},
	{1,b * b - a}
}
*/
void mul(ll c[][N], ll a[][N], ll b[][N]) {
	static ll tmp[N][N];
	memset(tmp, 0, sizeof tmp);
	for (int i = 0;i < N;i++) {
		for (int j = 0;j < N;j++) {
			for (int k = 0;k < N;k++) {
				(tmp[i][j] += a[i][k] % mod * b[k][j] % mod) %= mod;
			}
		}
	}
	memcpy(c, tmp, sizeof tmp);
}
int main() {
	ll a, b, n; scanf("%lld%lld%lld", &a, &b, &n);
	ll f[N][N] = { 2 * a, 2ll * a * a + 2ll* b };//n = 1
	ll A[N][N] = {
		{0,((b - a * a) % mod + mod) % mod},
		{1,2ll * a % mod}
	};
	n--;
	while (n) {
		if (n & 1) mul(f, f, A);
		mul(A, A, A);
		n >>= 1;
	}
	ll res = (f[0][0] % mod + mod) % mod;
	printf("%lld", res);
	return 0;
}